Hàm số logarit

HÀM SỐ LOGARIT

A. Lý thuyết

I. Định nghĩa
Cho số thực dương a khác 1. Hàm số $y={{\log }_{a}}x$ được gọi là hàm số logarit cơ số a
II. Đạo hàm
$y={{\log }_{a}}x\Rightarrow y'=\frac{1}{x\ln a}$

$y=\ln x\Rightarrow y'=\frac{1}{x}$

$y={{\log }_{a}}u(x)\Rightarrow y'=\frac{u'}{u\ln a}$

III. Bảng tóm tắt các tính chất của hàm số logarit $y={{\log }_{a}}x(a>0;a\ne 1)$

Tập xác định	$(0;+\infty )$
Đạo hàm
Chiều biến thiên	$a>1$: hàm số luôn đồng biến $0
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1;0) và ($a$;1); nằm phía bên phải trục tung, được biểu diễn ở hình 1.1 với hai trường hợp $a>1$ và $0<>

 

          hình 1.1

B. Ví dụ

Câu 1: Tập xác định D của hàm số $y=\log ({{x}^{2}}-4)$ là

                           

B. $D=(-\infty ;-2)\cup (2;+\infty )$

C. $D=(2;+\infty )$                                          

D. $D=(-2;2)$

Giải
Điều kiện: ${{x}^{2}}-4\ge 0\Leftrightarrow {{x}^{2}}\ge 4$
             $\Leftrightarrow x\in (-\infty ;-2)\cup (2;+\infty )$
Chọn B

Câu 2: Tập xác định của hàm số $y=\sqrt{\ln (x-10=\ln (x+1)}$ là

Giải
Điều kiện

Chọn D

Câu 3: Tính đạo hàm của hàm số sau $y=\ln (1+\sqrt{x+1})$

A. $y'=\frac{1}{2\sqrt{x+1}(1+\sqrt{x+1})}$                B. $y'=\frac{1}{1+\sqrt{x+1}}$

C. $y'=\frac{1}{\sqrt{x+1}(1+\sqrt{x+1})}$                  D. $y'=\frac{2}{\sqrt{x+1}(1+\sqrt{x+1})}$

Giải

$y'=\frac{(1+\sqrt{x+1})'}{1+\sqrt{x+1}}=\frac{\frac{1}{2\sqrt{x+1}}}{1+\sqrt{x+1}}=\frac{1}{2\sqrt{x+1}(1+\sqrt{x+1})}$

Chọn A
Câu 4: Đường cong trong hình dưới là đồ thị của 1 hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hàm hàm số đó là hàm số nào?

A. $y={{\log }_{0,5}}x$                                               B. $y={{\log }_{2}}x$

C.$y=-\frac{1}{3}x-\frac{1}{3}$                                            D. $y=-3x+1$

 Giải

Nhận thấy đây là đồ thị của hàm số logarit $y={{\log }_{a}}x$nên loại đáp án C, D.

Điểm A(2;-1)  thuộc  đồ thị hàm số nên:

$-1={{\log }_{a}}2={{a}^{-1}}=2\Rightarrow a=0,5$

Chọn A

Câu 5: Đồ thị hàm số$y=\left| {{\log }_{2}}(2x) \right|$ là hình nào trong bốn hình được liệt kê ở bốn phương án A, B, C, D dưới đây:

Giải

Đồ thị hàm số $y=\left| {{\log }_{2}}(2x) \right|$không có phần nằm dưới trục hoành nên loại đáp án C.

Hàm số$y=\left| {{\log }_{2}}(2x) \right|$ xác định với mọi $x>0$nên đồ thị hàm số$y=\left| {{\log }_{2}}(2x) \right|$ không cắt trục Oy.

Chọn  A

C.Bài tập tự luyện

Câu 1:  Tìm x để hàm số$y=\log \sqrt{{{x}^{2}}+x-12}$  xác định.

Câu 2: Tập xác định của hàm số $y=\frac{1}{\sqrt{2-x}}+\ln (x-1)$ là

    A. $D=(1;2)$      B. $D=(1;+\infty )$          C.$D=(0;+\infty )$            D.$D=\left[ 1;2 \right]$  

Câu 3: Cho hàm số $\ln x-\frac{1}{2}{{x}^{2}}+1$.Tìm giá trị lớn nhất 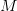  của hàm số trên $\left[ \frac{1}{2};2 \right]$

    A.$M=\ln 2-1$                                              B. $M=\frac{7}{8}-\ln 2$

    C.$M=\frac{7}{8}+\ln 2$                                             D. $M=\frac{1}{2}$

Câu 4: Đạo hàm của hàm số $y={{\log }_{3}}(x+1)-2\ln (x-1)+2x$tại điểm $x=2$ bằng

A. $\frac{1}{3}$                                             B. $\frac{1}{3\ln 3}+2$

C. $\frac{1}{3\ln 3}-1$                               D. $\frac{1}{3\ln 3}$

Câu 5: Tập xác định của hàm số $y=\sqrt{\frac{-{{\log }_{0,3}}(x-1)}{\sqrt{{{x}^{2}}-2x-8}}}$ là:

Câu 6: Tìm tất cả các giá trị thực của   để hàm số$y={{\log }_{a}}x(a>0;a\ne 1)$  có đồ thị là hình bên.

A. $a=\frac{1}{2}$                                     B. $a=1+\sqrt{2}$

C. $a=\sqrt{2}$                                D. $a=\frac{1}{\sqrt{2}}$

Câu 7: Hình bên là đồ thị của ba hàm số $y={{a}^{x}},y={{b}^{x}},y={{c}^{x}}(0

Khẳng định nào sau đây là khẳng định đúng?

    A. $a>b>c$      

    B. $b>a>c$

    C. $b>c>a$   

    D. $a>c>b$

Câu 8: Tính đạo hàm của hàm số $y={{\log }_{2018}}({{x}^{2}}+1)$

A. $y'=\frac{2x}{2018}$                                     B. $y'=\frac{2x}{({{x}^{2}}+1)2018}$

C. $y'=\frac{1}{({{x}^{2}}+1)2018}$                                    D. $y'=\frac{{{x}^{2}}}{({{x}^{2}}+1)2018}$

Câu 9: Tìm tập hợp các giá trị của tham số m để đồ thị hàm

số $y=\ln ({{x}^{2}}+1)+mx+1$  đồng biến trên 

    A. $[1;+\infty )$               B. $(1;+\infty )$                   C. $\left[ -1;1 \right]$                 D. $\left( -\infty ;-1 \right]$

Câu 10:  Xét các số thực $a,b$ thỏa mãn $a>b>1$ . Tìm giá trị nhỏ nhất ${{P}_{\min }}$  của biểu thức 

    A. ${{P}_{\min }}=19$           B. ${{P}_{\min }}=13$                 C. ${{P}_{\min }}=14$              D. ${{P}_{\min }}=15$

 

Đáp án bài tập tự luyện

1	2	3	4	5	6	7	8	9	10
A	A	D	D	A	C	B	B	A	D

 

Bài viết gợi ý: