Mở đầu về số phức.

Khái niệm cơ bản về số phức.

A. Lý thuyết

I. Khái niệm số phức

• Định nghĩa: Một số phức là một biểu tượng dạng a+bi, trong đó a và b là những số thực và số i thỏa mãn ${{i}^{2}}=-1$. Kí hiệu: z=a+bi.
• i được gọi là đơn vị ảo, a là phần thực (Re), b là phần ảo (Im).
• Tập hợp các số phức kí hiệu là C.
• Chú ý: Số phức có phần ảo bằng 0 gọi là số thực.

                        Số phức có phần thực bằng 0 gọi là số thuần ảo.

                        Số 0 vừa là số thực, vừa là số ảo.

• Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.

II. Biểu diễn hình học số phức

• Mỗi số phức z=a+bi được xác định bởi cặp số thực (a;b).
• Trên mặt phẳng Oxy, mỗi điểm M(a,b) được biểu diễn bởi một số phức và ngược lại.
• Mặt phẳng Oxy biểu diễn số phức được gọi là mặt phẳng phức. Gốc tọa độ O biểu diễn số 0, trục hoành Ox biểu diễn số thực, trục tung Oy biểu diễn số ảo.

 

III. Phép cộng và phép trừ số phức

1. Tổng của hai số phức

• Tổng của hai số phức z=a+bi và z’=a’+b’i (a,b,a’,b’$\in R$) là số phức z+z’=a+a’+(b+b’)i.

2. Tính chất của phép cộng số phức

• Tính chất kết hợp: (z+z’)+z’’=z+(z’+z’’) với mọi z, z’, z’’$\in C$.
• Tính chất giao hoán: z+z’=z’+z với mọi z, z’ $\in C$.
• Cộng với 0: z+0=0+z=z với mọi z$\in C$.
• Với mỗi số phức z=a+bi (a, b$\in R$) thì ta có: z+(-z)=0.
• Số - z được gọi là số đối của số phức z.

3. Phép trừ hai số phức

• Hiệu của hai số phức z và z’ là tổng của số phức z với –z’, tức là: z - z’ = z + (-z’).

IV. Phép nhân số phức

1. Tích của hai số phức

• Tích của hai số phức z=a+bi và z’=a’+b’i (a,b,a’,b’$\in R$) là số phức zz’=(a+bi)(a’+b’i)=aa’-bb’+(ab’+a’b)i.
• Chú ý: z.0=0 $\forall z\in C$.

2. Tính chất của phép nhân số phức

• Tính chất giao hoán: zz’=z’z với mọi z,z’$\in C$.
• Tính chất kết hợp: (zz’)z’’=z(z’z’’) với mọi z,z’, z’’$\in C$
• Nhân với 1: 1.z=z.1=z với mọi z$\in C$.
• Tính chất nhân phân phối (của phép nhân đối với phép cộng): z(z’+z’’)=zz’+zz’’ với mọi z,z’, z’’$\in C$.

V. Số phức liên hợp và mođun số phức

1. Số phức liên hợp

• Số phức liên hợp của z=a+bi (a, b$\in R$) là a-bi và được kí hiệu bởi $\overline{z}$.
• Chú ý: $\overline{\overline{z}}=z;\overline{z+{{z}^{,}}}=\overline{z}+\overline{{{z}^{,}}};\overline{z{{z}^{,}}}=\overline{z}.\overline{{{z}^{,}}}$

2. Môđun số phức

• Môđun của số phức z=a+bi (a, b$\in R$) là số thực không âm $\sqrt{{{a}^{2}}+{{b}^{2}}}$ và được kí hiệu là $\left| z \right|$.
• Nếu z=a+bi (a, b$\in R$) thì $\left| z \right|=\sqrt{z\overline{z}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$.

 

VI. Phép chia cho số phức khác 0.

1. Định nghĩa:

• Số nghịch đảo của số phức z khác 0 là số ${{z}^{-1}}=\frac{1}{{{\left| z \right|}^{2}}}\overline{z}$.
• Thương $\frac{z'}{z}$ của phép chia số phức z’ cho số phức z khác 0 là tích của z’ với số phức nghịch đảo của z, tức là $\frac{z'}{z}=z'{{z}^{-1}}$. Nếu $z\ne 0$thì $\frac{z'}{z}=\frac{z'\overline{z}}{{{\left| z \right|}^{2}}}$.
• Chú ý: Do $\frac{z'}{z}=\frac{z'\overline{z}}{{{\left| z \right|}^{2}}}=\frac{z'\overline{z}}{z\overline{z}}$ nên để tính \[\frac{z'}{z}\] ta chỉ việc nhân cả tử và mẫu với \[\overline{z}\].

 

B. Bài tập

I. Bài tập minh họa

Câu 1: Cho hai số  thực x, y thỏa mãn phương trình x+2i=3+4yi. Khi đó giá trị của x và y là:                    A. x=3, y=1          B. x=3i, y=2          C. x=3, $y=\frac{1}{2}$                   D. x=3, y=-1

 Lời giải: Chọn C.

Từ x+2i=3+4yi $\Rightarrow $$\Leftrightarrow $.

Câu 2: Phần thực và phần ảo của số phức z=1+2i lần lượt là:                    A. 2 và 1              B. 1 và 2i              C.  1 và 2     D. 1 và i

Lời giải: Chọn C.

Số phức z=1+2i có phần thực và phần ảo lần lượt là 1 và 2

Câu 3: Tìm tất cả các nghiệm của phương trình ${{z}^{2}}+2z+5=0$ trên tập số phức C.                    A. 1+2i; 1-2i         B. 1+i; 1-i.             C. -1+2i; -1-2i           D. -1+i; -1-i

Lời giải: Chọn C.

Cách 1: Giải tự luận: $\Delta '=1-5=-4=4{{i}^{2}}$. Giải tương tự như phương trình bậc hai trong tập số thực. Ta có nghiệm của phương trình là .

Cách 2: Ta nhập vào máy tính phương trình trên cũng sẽ ra được hai nghiệm như trên.

Cách 3: Sử dụng lệch CALC để thử từng đáp án.

Câu 4 (Đề thi 2018 mã 101): Có bao nhiêu số phức z thỏa mãn \[\left| z \right|\left( z-4-i \right)+2i=\left( 5-i \right)z\]                    A. 2                      B. 3                      C. 1                      D. 4

Lời giải: Chọn B.

Đối với dạng câu hỏi này, ta sẽ đưa về dạng \[f\left( \left| z \right| \right)=?\]

\[\left| z \right|\left( z-4-i \right)+2i=\left( 5-i \right)z\]\[\Leftrightarrow \left( \left| z \right|-5+i \right)z=4\left| z \right|+i\left( \left| z \right|-2 \right)\]

\[\Leftrightarrow \left| \left( \left| z \right|-5+i \right)z \right|=\left| 4\left| z \right|+i\left( \left| z \right|-2 \right) \right|\]

\[\Leftrightarrow \sqrt{{{\left( \left| z \right|-5 \right)}^{2}}+1}.\left| z \right|=\sqrt{16{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}\]

\[\Leftrightarrow \left( {{\left( \left| z \right|-5 \right)}^{2}}+1 \right).{{\left| z \right|}^{2}}=16{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}\]. Đặt \[\left| z \right|=t\left( t\ge 0 \right)\]. Phương trình tương đương:

\[{{t}^{4}}-10{{t}^{3}}+9{{t}^{2}}+4t-4=0\]\[\Leftrightarrow \]. Vậy có 3 giá trị t thỏa mãn điều kiện t>0. Nên có 3 số phức z thỏa mãn.

Câu 5: Điểm nào sau đây là điểm biểu diễn số phức z=(1+i)(2-i).             A. P     B. M    C. N    D. Q

Lời giải: Chọn D.

Ta bấm máy z=(1+i)(2-i)=3+i. Do đó Q là điểm biểu diễn số phức z.

Câu 6: Cho số phức z=2-3i. Môđun của số phức w=(1+i)z.                    A. $\left| \text{w} \right|=\sqrt{26}$               B. $\left| \text{w} \right|=\sqrt{37}$                    C. $\left| \text{w} \right|=5$        D. \[\left| \text{w} \right|=4\]

Lời giải: Chọn A.

w=(1+i)(2-3i)=5-i. Nên \[\left| \text{w} \right|=\sqrt{{{5}^{2}}+{{\left( -1 \right)}^{2}}}=\sqrt{26}\].

Câu 7: Cho z=mi, Tìm phần ảo của số phức \[\frac{1}{z}\]                    A. \[-\frac{1}{m}\]                          B. \[\frac{1}{m}\]              C. \[-\frac{1}{m}i\]                         D. \[\frac{1}{m}i\]

Lời giải: Chọn A.

\[\frac{1}{z}=\frac{1}{mi}=\frac{1}{mi.i}=-\frac{1}{m}i\].

Câu 8: Cho số phức z=a+bi \[\left( a,b\in R \right)\]. Khẳng định nào sau đây là sai?  A. \[\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\]          B. \[\overline{z}=a-bi\]             C. \[{{z}^{2}}\]là số thực            D. \[z\overline{z}\]là số thực

Lời giải: Chọn C.

Ta có: \[{{z}^{2}}={{\left( a+bi \right)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi\]. Nên \[{{z}^{2}}\]vẫn có thể là số ảo nên khẳng định C sai.

Câu 9: Trong mặt phẳng phức M là điểm biểu diễn cho số phức z=a+bi (a, b$\in R$\[,ab\ne 0\]). M’ là điểm biểu diễn cho số phức \[\overline{z}\]. Mệnh đề nào sau đây đúng? A. M’ đối xứng với M qua Oy. B. M’ đối xứng với M qua Ox. C. M’ đối xứng với M qua đường thẳng y=x. D. M’ đối xứng với M qua O.

Lời giải: Chọn B.

Vì M’ là điểm biểu diễn cho \[\overline{z}=a-bi\]. Nên M’(a;-b). Còn M(a;b). Vậy M và M’ đối xứng nhau qua Ox.

Câu 10: Trong tất cả các số phức z thỏa mãn \[\left| z-1+2i \right|=\left| z+3-4i \right|\]. Tìm giá trị nhỏ nhất của \[\left| z \right|\].                    A. \[\frac{5\sqrt{13}}{13}\]            B. \[2\sqrt{13}\]                   C. \[\sqrt{2}\]                            D. \[\sqrt{26}\]

Lời giải: Chọn A.

Cách 1 (giải tự luận):  Gọi z=x+yi.

\[\left| z-1+2i \right|=\left| z+3-4i \right|\]\[\Leftrightarrow \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}}=\sqrt{{{\left( x+3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}}\]

\[\Leftrightarrow 2x-3y+5=0\]\[\Leftrightarrow y=\frac{2x-5}{3}\]. Ta có: \[\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}\]\[=\frac{\sqrt{13{{\left( x-\frac{10}{13} \right)}^{2}}+\frac{225}{13}}}{3}\ge \frac{5\sqrt{13}}{13}\]. Vậy \[{{\left| z \right|}_{\min }}=\frac{5\sqrt{13}}{13}\].

Cách 2: Khi đã rút được y theo x. Ta có hàm \[f(x)=\sqrt{{{x}^{2}}+{{\left( \frac{2x-5}{3} \right)}^{2}}}\]. Ta dùng chức năng TABLE trong máy tính cũng sẽ tìm được min.

 

II. Bài tập tự luyện

Câu 1: Cho số phức z=1+2i. Số phức liên hợp của z là

                   A. \[\overline{z}\]= -1+2i               B. \[\overline{z}\]=-1-2i     C. \[\overline{z}\]=2+i               D. \[\overline{z}\]= 1-2i

Câu 2: Tìm tọa độ biểu diễn số phức \[z=\frac{\left( 2-3i \right)\left( 4-i \right)}{3+2i}\].

                   A. (-1;-4)              B. (1;4)                 C. (1;-4)                D. (-1;4)

Câu 3: Cho số phức \[{{z}_{1}}=3+2i\], \[{{z}_{2}}=6+5i\]. Tìm số phức liên hợp của số phức \[z=6{{z}_{1}}+5{{z}_{2}}\].

                   A. \[\overline{z}\]=51+40i              B. \[\overline{z}\]=51-40i   C. \[\overline{z}\]=48+37i         D. \[\overline{z}\]=48-37i

Câu 4: Tìm phần ảo số phức z, biết \[\left( 1+i \right)z=3-i\].

                   A. 2                      B. -2                     C. 1                      D. -1

Câu 5: Số phức nào sau đây thỏa \[\left| z \right|=\sqrt{5}\] và z là số thuần ảo.

                   A. \[z=\sqrt{5}\] B. \[z=-\sqrt{5}i\]                            C. z=5      D. z=3+i

Câu 6: Cho (16+2i)z+(17 +12i) \[\overline{z}\]=278+76i. Tìm \[\left| z \right|\].

                   A. 2                      B. 6                      C. 8                      D. 10

Câu 7: Cho số phức z=1+2i. Điểm nào dưới đây là điểm biểu diễn số phức w=z+i\[\overline{z}\]trên mặt phẳng tọa độ?

                   A. M(3;3)             B. Q(3;2)              C. N(2;3)              D. P(-3;3)

Câu 8:  Gọi \[{{z}_{1}}=3-i\] và \[{{z}_{2}}=4-i\]. Môđun số phức \[z_{1}^{2}+\overline{{{z}_{2}}}\] là

                   A. 12                    B. 10                     C. 13                    D. 15

Câu 9: Cho số phức z=a+bi với a, b là số thực bất kì. Mệnh đề nào sau đây đúng?

A. Phần ảo của z là bi.

B. Môđun của \[{{z}^{2}}={{a}^{2}}+{{b}^{2}}\].

C. \[z-\overline{z}\]không phải là số thực.

D. Số z và \[\overline{z}\] có môđun khác nhau.

Câu 10: Điểm M trong hình vẽ dưới đây biểu thị cho số phức

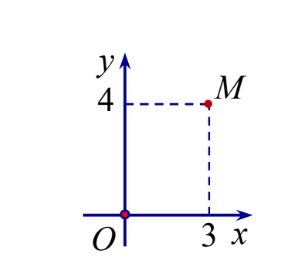
                   A. 3-4i                  B.-2+3i                  C. 3+4i                 D. 3+2i

Câu 11: Cho số phức z thỏa mãn các điều kiện \[\left| z+8-3i \right|=\left| z-i \right|\] và\[\left| z+8-7i \right|=\left| z+4-i \right|\]. Tìm số phức w=z+7-3i.

                   A. w=3-i               B. w=13-6i            C. w=1+i              D. w=4+3i

Câu 12: Cho \[{{z}_{1}},{{z}_{2}}\] là hai số phức thỏa mãn\[{{z}^{2}}-z+2=0\]. Tìm phần ảo của số phức \[\text{w}={{\left[ \left( 1-{{z}_{1}} \right)\left( 1-{{z}_{2}} \right) \right]}^{2018}}\].

                   A. 0                      B. 2                      C. 8                      D. 10

Câu 13: Có bao nhiêu số phức thỏa mãn \[z+{{\left| z \right|}^{2}}.i-1-\frac{3}{4}i=0\].

                   A. 1                      B. 3                      C. 2                      D. 0

Câu 14: Trong mặt phẳng phức, xét M(x;y) là điểm biểu diễn số phức z=x+yi thỏa mãn \[\frac{z+i}{z-i}\] là số thực. Tâp hợp các điểm M là

A. Parabol.

B. Elip.

C. Tập hợp các điểm trên trục hoành trừ điểm có tọa độ (1;0).

D. Tập hợp các điểm trên trục tung trừ điểm có tọa độ (0;1).

Câu 15: Biết z là một nghiệm của phương trình \[z+\frac{1}{z}=1\]. Tính giá trị biểu thức \[P={{z}^{3}}+{{\left( \frac{1}{z} \right)}^{3}}\].

                   A. P=-2                 B. P=0                  C. P=4                  D.P=1

Câu 16:Tập hợp điểm biểu diễn số phức z thỏa mãn \[\left| \frac{z}{z-i} \right|=3\] là đường nào?

A. Một đường thẳng.

B. Một đường parabol.

C. Một đường tròn.

D. Một đường elip.

Câu 17: Cho hai số phức \[{{z}_{1}},{{z}_{2}}\] thỏa mãn \[{{z}^{2}}=119-120i\]. Tính\[{{\left| {{z}_{1}}-{{z}_{2}} \right|}^{2}}\]

                   A. 676                  B. 156                   C. 234                  D. 434

Câu 18: Có bao nhiêu số phức z thỏa mãn \[\left| z+2+3i \right|=5\] và \[\frac{z}{z-2}\] là số thuần ảo.

                   A. 1                      B. 2                      C. 3                      D. 5

Câu 19: Cho số phức z=a+bi thỏa mãn\[z+1+3i-\left| z \right|i=0\]. Tính S=a+3b.

                   A. S=-5                 B. S=2                   C. S=5                  D. S=6

Câu 20: trong các số phức z thỏa mãn điều kiện \[\left| z+3i \right|=\left| z+2-i \right|\]. Tìm z để \[{{\left| z \right|}_{\min }}\].

                   A.z=1-2i               B. z=1+2i              C. \[z=\frac{1}{5}-\frac{2}{5}i\]                          D. z= -1+2i

Đáp án bài tập tự luyện:

Bài viết gợi ý: