Chuyên đề: Ứng dụng tích phân giải các bài toán thực tế.

Chuyên đề: Ứng dụng tích phân giải các bài toán thực tế.

A. Lý thuyết

I. Các bài toán vật lý

Các bài toán vật lý chủ yếu xoay quanh việc tính quãng đường, vận tốc, gia tốc của vật. Vì vậy, ta có mối liên hệ giữa các đại lượng trên như sau: $\int{a(t)dt=v(t)+C}$; $\int{v(t)dt=s(t)+C}$.
Chủ yếu đề thi sẽ xoay quanh việc ứng dụng tích phân bằng cách hỏi tính quãng đường, vận tốc, gia tốc khi cho biết thời gian. Đôi khi khó hơn khi đề bài yêu cầu học sinh chọn mốc thời gian trước khi tính các đại lượng trên.

II. Các bài toán hình học

1. Ứng dụng tích phân tính diện tích

Nếu hàm số y=f(x) liên tục trên [a;b] thì diện tích được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a, x=b (a

Diện tích hình phẳng được giới hạn bởi các đồ thị hàm số y=f(x), y=g(x) và hai đường thẳng x=a, x=b (a

2. Ứng dụng tích phân tính thể tích vật thể

Thể tích vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a, b là $V=\int\limits_{a}^{b}{S(x)d\text{x}}$. Trong đó S(x) là diện tích của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ thuộc [a,b].

Thể tích vật thể tròn xoay được tạo thành bởi đồ thị hàm số y=f(x) khi xoay quanh trục Ox và bị giới hạn bởi [a,b] là $V=\pi \int\limits_{a}^{b}{{{f}^{2}}(x)d\text{x}}$.
Thể tích vật thể tròn xoay được tạo thành bởi đồ thị hàm số y=f(x) và y=g(x) khi xoay quanh trục Ox được giới hạn bởi [a,b] là $V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}(x)-{{g}^{2}}(x) \right|d\text{x}}$.
Chú ý: Đa số bài toán thường tính theo công thức $V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}(x)-{{g}^{2}}(x) \right|d\text{x}}$, đôi khi đòi hỏi học sinh nắm vững lý thuyết thì ra đề theo công thức $V=\int\limits_{a}^{b}{S(x)d\text{x}}$. Tuy nhiên, đối với những bài toán vận dụng cao thì thường phải chia nhỏ hình để tính sẽ phức tạp hơn đòi hỏi học sinh nắm chắc lý thuyết và công thức.
Các công thức trên tương tự khi xoay quanh trục Oy.

B. Bài tập

I. Bài tập minh họa

Câu 1 (Đề thi ĐH 2018 mã 101): Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật $v(t)=\frac{1}{180}{{t}^{2}}+\frac{11}{18}t$(m/s), trong đó t là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng a (là hằng số). Sau khi B xuất phát được 10 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng

A. 22 B. 15 C. 10 D. 7

Lời giải: Chọn B.

Ta có vận tốc của B tại thời điểm t là $\int{a\text{d}t=at+C}$. Mà B xuất phát từ trạng thái nghỉ nên tại t=0 thì v=0. Suy ra C=0 . Vậy ${{v}_{B}}=at$.

Tại thời điểm gặp nhau, quãng đường hai vật đi được là S=$\int\limits_{0}^{15}{v(t)dt}=\int\limits_{0}^{15}{\left( \frac{1}{180}{{t}^{2}}+\frac{11}{18}t \right)}dt=75$.

Mà $S=\int\limits_{0}^{10}{{{v}_{B}}}dt=75$ $$$\Leftrightarrow \int\limits_{0}^{10}{at\text{d}t}=75\Leftrightarrow \mathop{\left. \frac{a{{t}^{2}}}{2} \right|}_{0}^{10}=75$ . Suy ra a=1,5. Nên v=at=1,5.10=15m/s.

Câu 2: Một người chạy có v(t) phụ thuộc thời gian có đồ thị là 1 phần parapol có đỉnh $I\left( \frac{1}{2};8 \right)$ như hình vẽ. Tính quãng đường người đó chạy trong 1h.

A. 5,3 B. 2,3 C. 1,3 D. 3,3

Lời giải: Chọn A.

Gọi $y=a{{x}^{2}}+bx+c$. Đồ thị hàm số qua điểm x=0 thì y=0. Nên c=0.

Có tọa độ đỉnh là $I\left( \frac{1}{2};8 \right)$ $\Rightarrow $ $\Rightarrow $ $\Rightarrow y=-32{{\text{x}}^{2}}+32\text{x}$

$S=\int\limits_{0}^{1}{\left( -32{{\text{x}}^{2}}+32\text{x} \right)d\text{x}}=\frac{16}{3}\approx 5,3$.

Câu 3: Một ô tô đang chuyển động với vận tốc 12m/s thì người lái xe bất ngờ tăng tốc cho xe chạy nhanh dần đều, sau 15s thì xe đạt vận tốc 15m/s. Tính quãng đường xe đi được sau 30s kể từ khi tăng tốc.

A. 270 B. 450 C. 360 D. 540

Lời giải: Chọn B.

Gọi gia tốc của ô tô khi tăng tốc là a (hằng số). Theo đề bài ta có: $12+\int\limits_{0}^{15}{a\text{d}t}=15\Leftrightarrow a=\frac{1}{5}$.

Sau khi tăng tốc thì $v=\int{a\text{d}t}=at+C$. Vì tại t=0 ( lúc ô tô tăng tốc) thì v=12m/s. Nên C=12.

Vậy $v=\frac{1}{5}t+12$. Nên quãng đường đi được trong 30s là: $\Rightarrow s=\int\limits_{0}^{30}{\left( \frac{1}{5}t+12 \right)}dt=450m$.

Câu 4: Một người muốn làm cái bảng hiệu là 1 phần của elip có kích thước hình dạng giống như hình vẽ. Tính diện tích cái biển đó.

A. 1,3 B. 1,4 C. 1,5 D. 1,6

Lời giải: Chọn B.

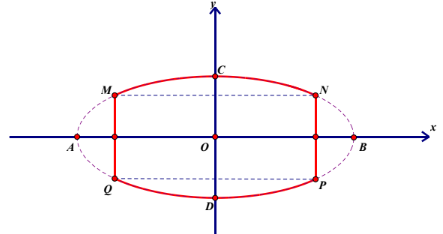
Elip có phương trình:$\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1$.

Theo hình đề bài, ta có độ dài $OC=\frac{1}{2}$(nửa trục nhỏ của elip) $\Rightarrow b=\frac{1}{2}$.

Và điểm $N\left( \frac{3}{4};\frac{3}{8} \right)$ thuộc elip $\Rightarrow $ $\Rightarrow {{a}^{2}}=\frac{9}{7}$. Vậy elip: $\Leftrightarrow y=\pm \frac{1}{2}\sqrt{1-\frac{7}{9}{{x}^{2}}}$.

Vì phần dương và âm của elip đối xứng nhau qua Ox nên chúng có diện tích bằng nhau. Nên để đơn giản việc tính toán, ta sẽ tính diện tích phần dương rồi nhân đôi.

$S=2\int\limits_{-0,75}^{0,75}{\frac{1}{2}\sqrt{1-\frac{7}{9}{{x}^{2}}}d\text{x}\approx \text{1,4}}$.

Câu 5: Trong Công viên toán học có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương trình trong hệ tọa độ Oxy là $16{{y}^{2}}={{x}^{2}}\left( 25-{{x}^{2}} \right)$ như hình vẽ. Tính diện tích của mảnh đất trên.

A. $\frac{125}{6}$ B. $\frac{125}{4}$ C. $\frac{250}{3}$ D. $\frac{125}{3}$

Lời giải: Chọn D

Ta tìm giao điểm của đường Lemmiscate với trục Ox: ${{x}^{2}}\left( 25-{{x}^{2}} \right)=0\Leftrightarrow $

Từ phương trình $16{{y}^{2}}={{x}^{2}}\left( 25-{{x}^{2}} \right)$\[\Leftrightarrow y=\pm \frac{1}{4}x\sqrt{25-{{x}^{2}}}\]. Để đơn giản, ta sẽ tính diện tích phần dương 1 phần rồi nhân 4: \[S=4\int\limits_{0}^{5}{\frac{1}{4}x\sqrt{25-{{x}^{2}}}d\text{x}}\]\[=\frac{125}{3}\].

Câu 6: Một thùng rượu có bán kính đáy là 30cm, thiết diện vuông góc với trục cách đều hai đáy có bán kính 40cm, chiều cao là 1m. Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol. Hỏi thể tích thùng rượu là bao nhiêu lít?

A. 425,2 B. 425162 C. 212581 D. 212,6

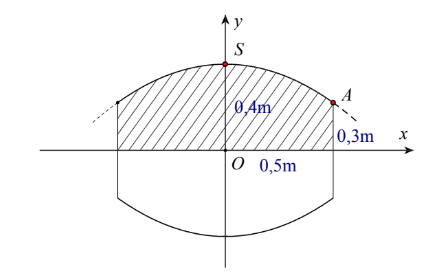Lời giải: Chọn A.

Gọi phương trình parabol nằm trên là \[y=a{{x}^{2}}+bx+c\]. Parabol đi qua điểm \[\text{A}\left( \frac{1}{2};\frac{3}{10} \right)\] và nhận \[I\left( 0;\frac{2}{5} \right)\] làm đỉnh.

\[\Rightarrow \] \[\Leftrightarrow \] . Vậy parabol là: \[y=-\frac{2}{5}{{x}^{2}}+\frac{2}{5}\].

Vậy \[V=\pi \int\limits_{-0,5}^{0,5}{{{\left( -\frac{2}{5}{{x}^{2}}+\frac{2}{5} \right)}^{2}}}\]\[=\frac{203\pi }{1500}{{m}^{3}}\]\[\approx 425,2\] (lít).

Câu 7: Một cái phao có kích thước như hình vẽ. Tính thể tích hình đó theo R và r.

A. \[V=2{{\pi }^{2}}{{r}^{2}}R\] B. \[V=2{{\pi }^{2}}r{{R}^{2}}\]

C. \[V={{\pi }^{2}}r{{R}^{2}}\] D. \[V={{\pi }^{2}}{{r}^{2}}R\]

Lời giải: Chọn A.

Gắn hệ trục tọa độ như hình vẽ:

Ta có phương trình đường tròn là:\[{{\left( x-R \right)}^{2}}+{{y}^{2}}={{r}^{2}}\]\[\Rightarrow x=R\pm \sqrt{{{r}^{2}}-{{y}^{2}}}\].

\[V=\pi \int\limits_{-r}^{r}{\left[ {{\left( R+\sqrt{{{r}^{2}}-{{y}^{2}}} \right)}^{2}}-{{\left( R-\sqrt{{{r}^{2}}-{{y}^{2}}} \right)}^{2}} \right]}dy\]

\[=\pi \int\limits_{-r}^{r}{4\text{R}\sqrt{{{r}^{2}}-{{y}^{2}}}dy}\]. Đặt y=rsint\[\Leftrightarrow dy=r\cos tdt\]. Đổi cận \[-r\to \frac{-\pi }{2}\]; \[r\to \frac{\pi }{2}\].

\[\Rightarrow V=\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{4\text{R}\sqrt{{{r}^{2}}\left( 1-{{\sin }^{2}}t \right)}.r\cos tdt}\]=\[\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{4\text{R}.{{r}^{2}}{{\cos }^{2}}tdt}\]=\[2{{\pi }^{2}}{{r}^{2}}R\].

Câu 8: Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng \[N'(t)=\frac{4000}{1+0,5t}\] và lúc đầu đám vi trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng gần với số nào sau đây nhất.

A. 251000 B. 264334 C. 261000 D. 274334

Lời giải: Chọn B

Số lượng vi trùng ngày thứ t là: \[N(t)=\int{\frac{4000}{1+0,5t}dt}\]\[=\int{\frac{8000}{1+0,5t}d\left( 1+0,5t \right)}\]=8000ln(1+0,5t)+C.

Tại t=0 suy ra C=250000.Vậy N(t)=8000ln(1+0,5t)+250000. Suy ra N(10)\[\approx \]264334.

II. Bài tập tự luyện

Câu 1: Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc \[a(t)=3t+{{t}^{2}}\]. Tính quãng đường( tính theo m) vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.

A. \[\frac{4300}{3}\] B. 4300 C. 430 D. \[\frac{430}{3}\]

Câu 2: Dòng điện xoay chiều hình sin chạy qua mạch LC có biểu thức cường độ là \[i\left( t \right)={{I}_{0}}\cos \left( wt-\frac{\pi }{2} \right)\]. Biết i=q’ với q là điện tích tức thời ở tụ điện. Tính từ lúc t=0, điện lượng chuyển qua dây dẫn trong thời gian \[\frac{\pi }{\text{w}}\] là

A. \[\frac{\pi \sqrt{2}{{I}_{0}}}{\text{w}}\] B. 0 C. \[\frac{2{{I}_{0}}}{\text{w}}\] D. \[\frac{\pi {{I}_{0}}}{\text{w}\sqrt{2}}\]

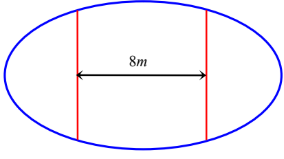Câu 3: Vườn hoa nhà trường hình elip có trục lớn dài 16m, trục bé dài 10m. Nhà trường muốn trồng hoa trên dải đất rộng 8m như hình vẽ. Biết 100.000 đồng/\[{{m}^{2}}\]. Hỏi kinh phí trồng hoa là bao nhiêu?

A.7.862.000 B. 7.653.000 C. 7.128.000 D. 7.826.000

Câu 4: Vòm cửa lớn của 1 trung tâm văn hóa có dạng hình parapol. Hãy tính diện tích mặt kính cần lắp vào biết rằng vòm cửa cao 8m và rộng 8m.

A. \[\frac{28}{3}\] B. \[\frac{26}{3}\]

C.\[\frac{128}{3}\] D. \[\frac{131}{3}\]

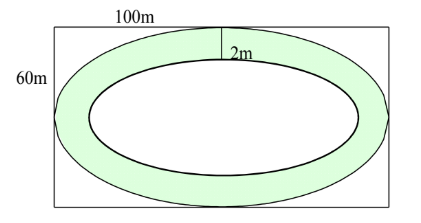Câu 5: Một sân chơi có hình chữ nhật dài 100m, rộng 60m, người ta làm 1 con đường trong sân như hình vẽ. Biết viền ngoài và trong của con đường là 2 elip. Elip ngoài có trục lớn và trục bé song song với các cạnh hình chữ nhật và chiều rộng mặt đường là 2m. Biết 600.000 đ/\[{{m}^{2}}\]. Tính số tiền làm đường (làm tròn đến hàng nghìn).

A. 293904000 B.294053000 C. 244365672 D.234756865

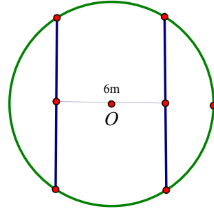Câu 6: Một mảnh vườn hình tròn tâm O bán kính 6m. Kinh phí trồng cây là 70000 đ/\[{{m}^{2}}\]. Hỏi cần bao nhiêu tiền để trồng cây trên mảnh đất đó (số tiền làm tròn đến hàng đơn vị).

A. 4821322 B. 4546724

C. 4098995 D. 4098677

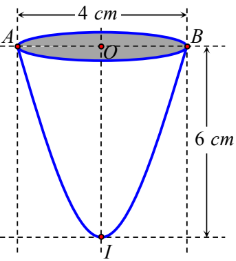
Câu 7: Có 1 cái ly nư hình vẽ. Người ta đo được đường kính của miệng ly là 4cm và chiều cao là 6cm. Biết thiết diện của chiếc ly cắt bởi mặt phẳng đối xứng parabol. Tính thể tích ly.

A. \[12\pi \] B. 12 C. 72 D. \[72\pi \]

Câu 8: Gọi (H) là phần giao của hai khối \[\frac{1}{4}\] hình trụ có bán kính a, hai trục hình trụ vuông góc với nhau. Tính thể tích (H).

A. \[\frac{2{{\text{a}}^{3}}}{3}\] B. \[\frac{\text{3}{{\text{a}}^{3}}}{4}\] C. \[\frac{{{\text{a}}^{3}}}{4}\] D. \[\frac{\pi {{\text{a}}^{3}}}{4}\]

Câu 9: Tại một xã xây 1 cây cầu bê tông như hình vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu (đường cong trong hình là đường parapol).

A. 19 B. 21 C. 18 D. 40

Câu 10: Một người thợ gốm làm 1 cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \[y=\sqrt{x+1}\] và trục Ox. Biết đáy và miệng lọ có đường kính lần lượt là 2dm và 4dm, thể tích lọ là.

A. 8 B. \[\frac{15\pi }{2}\] C. \[\frac{14\pi }{3}\] D. 12

Đáp án bài tập tự luyện: