CHỨNG MINH 3 ĐƯỜNG THẲNG ĐỒNG QUY
PHƯƠNG PHÁP
|
Muốn chứng minh 3 đường thẳng ${{d}_{1}},{{d}_{2}},{{d}_{3}}$ đồng quy tại 1 điểm I . Bước 1 : Chứng minh :${{d}_{1}}\cap {{d}_{2}}=\left\{ I \right\}$ Bước 2 : Chứng minh : $I\in {{d}_{3}}$ |
VÍ DỤ MINH HỌA
Ví dụ 1. Cho chóp S.ABCD có AB không song song với CD, M là trung điểm SC
a ) Tìm giao điểm N của SD và (ABM)
b) Gọi O là giao của AC và BD. Chứng minh SO, AM , BN đồng quy
Lời giải.
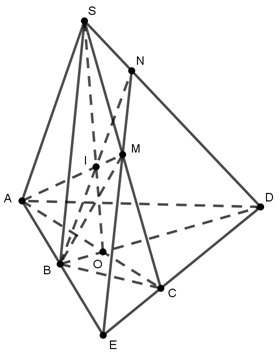
a) Chọn mp phụ chứa SD là mp(SCD). Tìm giao tuyến của 2 mp (ABM) và (SCD).
Gọi AB cắt CD tại E. Khi đó : E là điểm chung của 2 mp
Mà M cũng là điểm chung của 2 mp nên ME chính là giao tuyến của 2 mp.
Vậy N chính là giao điểm của SD và ME.
b) Trong mp(SAC) gọi AM cắt SO tại I. Ta chứng minh : I, B, N thẳng hàng. Thật vậy ;
Ta có : B, N là điểm chung của 2 mp (ABM) và (SBD), lại có từ câu a) thì I cũng là điểm chung của 2 mp này.
Vậy I, B, N thẳng hàng.
Ví dụ 2. Cho chóp S.ABCD có AB giao CD tại E . I , J là trung điểm của SA , SB . Lấy N tùy ý trên SD
a) Tìm giao điểm M của SC và (IJN)
b) Chứng minh rằng : IJ, MN, SE đồng quy
Lời giải.
.png)
a) Chọn mp phụ chứa SC là mp(SAC). Tìm giao tuyến của mp (SAC) và (IJN).
Gọi AC cắt BD tại O. Trong mp(SBD), gọi NJ cắt SO tại F
Khi đó : F là điểm chung của 2 mp (SAC) và (IJN), mà I là điểm chung của 2 mp này nên FI chính là giao tuyến của 2 mp.
Vậy M chính là giao điểm của SC và FI.
b) Trong mp(SDE), gọi MN cắt SE tại G. Khi đó : I, J, G là 3 điểm chung của 2 mp (SAE) và (IJN). Vậy I, J, G thẳng hàng hay IJ, MN, SE đồng quy tại G.
BÀI TẬP TỰ LUYỆN
Bài 1. Cho tứ diện ABCD. Gọi E, F, G là các điểm lần lượt thuộc các cạnh AB, AC, BD sao cho EF cắt BC tại I, EGcắt AD tại H. Chứng minh ba đường thẳng CD, IG, HF đồng quy?
Bài 2. Cho hình chóp S.ABCD có đáy ABCD không phải là hình thang. Trên cạnh SC lấy điểm M. Gọi N là giao điểm của đường thẳng SD với mặt phẳng (AMB). Chứng minh ba đường thẳng AB, CD, MN đồng quy.
Chúc các bạn học tốt, thân!







