THIẾT DIỆN
I. Khái niệm thiết diện
Các đoạn giao tuyến giữa mặt phẳng và hình chóp khi nối tiếp nhau sẽ tạo thành một đa giác phẳng, người ta gọi đó là thiết diện (hay mặt cắt) của mặt phẳng với hình chóp đó.
II. Các định lý cần áp dụng để tìm thiết diện của mặt phẳng và hình chóp
Để tìm được thiết diện của mặt phẳng và hình chóp ta dựa vào định nghĩa, tức là tìm các đoạn giao tuyến nối tiếp nhau bằng cách sử dụng các định lý được ghi dưới đây
– Định lý về đường thẳng song song với mặt phẳng: (a // (Q), a ⊂ (P), (P) ∩ (Q) = b) ⇒ a // b
– Định lý về hai mặt phẳng song song: (P) // (Q), (R) ∩ (P) = a, (R) ∩ (Q) = b ⇒ a // b
– Định lý về hai mặt phẳng giao nhau: (Q) ∩ (R) = a, (P) // a) và ((Q) ∩ (P) = d, (R) ∩ (P) = d’ ⇒ d//d’
Tùy theo tính chất của mặt phẳng (P), chọn một mặt của khối đa diện để vẽ giao tuyến của mặt phẳng (P) với mặt đó. Giao tuyến này còn gọi là giao tuyến gốc (giao tuyến này thường dễ dàng tìm được từ giả thiết).
Xác định giao điểm của giao tuyến đã dựng với các cạnh còn lại của khối đa diện trong các mặt phẳng vừa chọn.
Từ các giao điểm trên, dựa vào tính chất của mặt phẳng (P) để vẽ các giao tuyến với các mặt còn lại.
Phương pháp xác định : Thiết diện được xác định bằng cách tìm các giao tuyến của các mặt khối chóp với mặt phẳng cần tìm thiết diện. Hay nói cách khác bài toán tìm thiết diện cũng chính là bài toán tìm giao điểm của đường thẳng với mặt phẳng.
III. Ví dụ minh họa
Ví dụ 1. Cho hình chóp SABC, M là trung điểm SA, G là trọng tâm tam giác SAB. Tìm thiết diện tạo bởi hình chóp và CMG.
Lời giải.
.png)
Xét tam giác SAB có đường trung tuyến BM và G là trọng tâm nên B, G, M thẳng hàng.
Khi đó mp(CMG) chính là mp(BCM).
Nhận xét : mp(BCM) cắt các cạnh của hình chóp tại các điểm B, C, M nên thiết diện tạo bởi hình chóp và CMG là tam giác BCM.
Ví dụ 2. Cho hình chóp SABCD, M là trung điểm SA, N thuộc SB sao cho SN = 2 NB. Tìm thiết diện của chóp và DMN.
Lời giải.
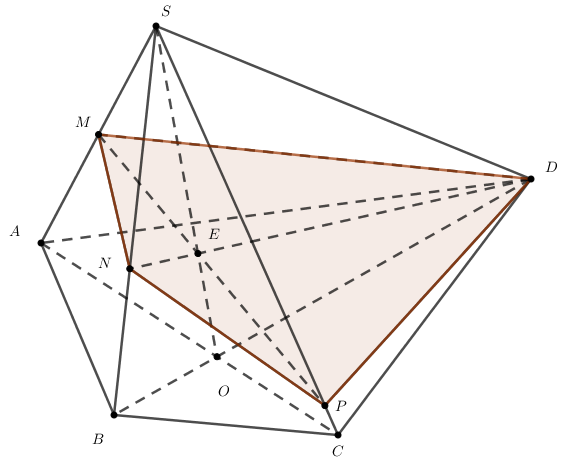
Tìm giao điểm của SC và mp(DMN) :
Chọn mp phụ chứa SC là mp(SAC). Tìm giao tuyến của mp(SAC) và mp(DMN).
Gọi AC cắt BD tại O. Trong mp(SBD), gọi DN cắt SO tại E. Khi đó : E là điểm chung của mp(DMN) và mp(SAC).
Lại có M cũng là điểm chung của 2 mp (DMN) và (SAC). Khi đó : EM chính là giao tuyến của 2 mp.
Vậy giao điểm của SC và mp(DMN) chính là giao điểm P của SC và EM (như hình vẽ).
Như vậy, ta nhận được thiết diện cần xác định là tứ giác DMNP.
Ví dụ 3. Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi M là trung điểm của SB, G là trọng tâm Tam giác SAD.
a) Tìm giao điểm I của GM với (ABCD).
b) Tìm thiết diện của hình chóp với (AGM)
Lời giải.
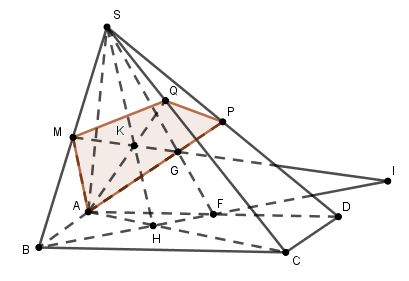
a) Gọi SG ∩ AD = {F}
Trong mp(SBF), gọi MG cắt BF tại I - chính là điểm cần tìm (vì I thuộc MG và I thuôc BF ⊂ (ABCD).
b) Ta có :
mp(AMG) ∩ mp(SAB) = AM
mp(AMG) ∩ mp(SAD) = AP (với P là trung điểm của SD)
Cần xác định giao điểm của SC với mp(AMG). Chọn mp phụ chứa SC là mp(SAC).
Ta cần tìm giao tuyến của (SAC) và (AMG).
Gọi AC ∩ BI = {H}; SH ∩ MG = {K}. Suy ra K là điểm chung của 2 mp.
mà A cũng là điểm chung của mp nên giao tuyến: (SAC) ∩ (AMG) = AK
Trong (SAC) gọi AK ∩ SC = {Q}
Vậy Q giao của SC với (AMG)
Thiêt diện là tứ giác: AMQP
Ví dụ 4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a Các điểm M, N, P lần lượt là trung điểm của SA, SB, SC Mặt phẳng (MNP) cắt hình chóp theo một thiết diện. Tính diện tích thiết diện đó.
Lời giải.
.png)
.png)
IV. Bài tập vận dụng
Bài 1. Cho hình chóp S.ABCD. Gọi M, N lần lượt là điểm lấy trên AD và DC. E là điểm nằm trên đường thẳng SD và nằm ngoài đoạn SD nhưng gần D . Tìm thiết diện của hình chóp với mặt phẳng (MNE).
Bài 2. Cho tứ diện ABCD . Gọi H,K lần lượt là trung điểm các cạnh AB, BC . Trong đoạn thẳng CD lấy điểm M sao cho KM không song song với BD . Tìm thiết diện của tứ diện với (HKM ).
Bài 3. Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N , I là ba điểm lấy trên AD ,CD , SO . Tìm thiết diện của hình chóp với mặt phẳng (MNI).
Bài 4. Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện. Tính diện tích thiết diện đó.
Chúc các bạn học tốt, thân!







