Phép đồng dạng

PHÉP ĐỒNG DẠNG

A. Lý thuyết

1. Định nghĩa

Một phép biến hình F được gọi là phép biến hình tỉ số k (k > 0) nếu với hai điểm bất kì M, N và ảnh ${{M}^{'}},{{N}^{'}}$ tương ứng của chúng ta luôn có ${{M}^{'}}{{N}^{'}}=k.MN$ .

Nhận xét:

Phép dời hình là phép đồng dạng tỉ số $k=1$
Phép vị tự tỉ số k là phép đồng dạng tỉ số $\left| k \right|$
Nếu thực hiện liên tiếp hai phép đồng dạng thì ta được một phép đồng dạng

2. Tính chất

Phép đồng dạng tỉ số k:

Biến ba điểm thẳng hang thành ba điểm thẳng hang và bảo toàn thứ tự giữa chúng
Biến một đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng
Biến một tam giác thành tam giác dồng dạng với tam gaisc đã cho, biến góc thành góc bằng nó
Biến mộ đường tròn bán kính R thành đường tròn bán kính $k.R$

3. Hình đồng dạng

Hai hình được gọi là hình đồng dạng với nhau nếu có moọt phép đồng dạng biến hình này thành hình kia

B. Bài tập minh họa

Câu 1 : Trong các mệnh đề sau mệnh đề nào sai?

A. Hai đường thẳng baatss kì luôn đồng dạng

B. Hai dường tròn bất kì luôn đồng dạng

C. Hai hình vuông bất kì luôn đồng dạng

D. Hai hình chữ nhật bất kì luôn đồng dạng

Giải:

Với hai hình chữ nhật bất kì ta chọn từng cặp cạnh tương ứng, khi đó tỉ lệ giữa chúng chưa chắc đãn bằng nhau

$\Rightarrow $ Không tồn tại phép đồng dạng biến hình chữ nhật này thành hình chứ nhật kia

Chọn D

Câu 2 : Cho tam giác \[ABC\] và \[A'B'C'\] đồng dạng với nhau theo tỉ số \[k\]. Mệnh đề nào sau đây là sai?

A. \[k\] là tỉ số hai trung tuyến tương ứng

B. \[k\] là tỉ số hai đường cao tương ứng

C. \[k\] là tỉ số hai góc tương ứng

D. \[k\]là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng

Giải:

Vì hai tam giác đồng dạng thì các góc tương ứng luôn bằng nhau

Chọn C

Câu 3: Trong mặt phẳng tọa độ \[Oxy\] cho điểm $M\left( 2;4 \right).$ Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm $O$ tỉ số $k=\frac{1}{2}$ và phép đối xứng qua trục $Oy$ sẽ biến $M$ thành điểm nào trong các điểm sau:

A.$\left( 1;2 \right)$ B.$\left( -2;4 \right)$ C.$\left( -1;2 \right)$ D.$\left( 1;-2 \right)$

Giải:

Gọi

Chọn C

Câu 4: Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $d$ có phương trình $x+y-2=0.$ Viết phương trình đường thẳng $d'$ là ảnh của $d$ qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm $I\left( -1;-1 \right)$ tỉ số $k=\frac{1}{2}$ và phép quay tâm $O$ góc $-{{45}^{0}}.$

A.$y=0.$ B.$x=0.$ C.$y=x.$ D.$y=-x.$

Giải:

Gọi ${{d}_{1}}$ là ảnh của $d$ qua phép vị tự tâm $I\left( -1;-1 \right)$ tỉ số $k=\frac{1}{2}.$

Vì ${{d}_{1}}$ song song hoặc trùng với $d$ nên phương trình của nó có dạng $x+y+c=0.$

Lấy $M\left( 1;1 \right)$ thuộc $d.$

Gọi

Vậy phương trình của ${{d}_{1}}$ là $x+y=0.$

Ảnh của ${{d}_{1}}$ (đường phân giác góc phần tư thứ hai) qua phép quay tâm $O$ góc $-{{45}^{0}}$ là đường thẳng $Oy.$ Vậy phương trình của $d'$ là $x=0.$

Chọn B

Câu 5: Trong mặt phẳng tọa độ $Oxy$ cho đường tròn $\left( C \right)$ có phương trình ${{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4.$ Phép đồng dạng có được bằng cách thực hiện liên tiếp các phép vị tự có tâm $O$ tỉ số $k=\frac{1}{2}$ và phép quay tâm $O$ góc ${{90}^{0}}$ sẽ biến $\left( C \right)$ thành đường tròn nào trong các đường tròn sau?

A. ${{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=1.$ B. ${{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1.$

C. ${{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1.$ D. ${{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1.$

Giải:

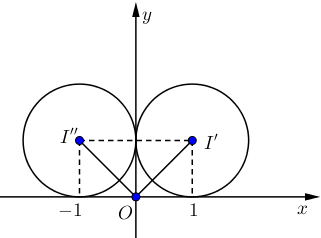
Đường tròn $\left( C \right)$ có tâm $I\left( 2;\,2 \right),$ bán kính $R=2.$

Suy ra phép vị tự ${{V}_{\left( O;\,\frac{1}{2} \right)}}$ biến $\left( C \right)$ thành $\left( {{C}'} \right)$ tâm ${I}'\left( 1;\,1 \right),$ bán kính ${R}'=1.$

Phép quay ${{Q}_{\left( O;\,{{90}^{0}} \right)}}$ biến $\left( {{C}'} \right)$ thành $\left( {{C}''} \right)$ có tâm $I''\left( -1;1 \right)$, bán kính $R''=R'=1.$

Vậy phương trình đường tròn $\left( {{C}''} \right)$ là ${{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1$.

Chọn D

Câu 6: Trong mặt phẳng tọa độ $Oxy$ cho hai điểm $A\left( -\,2;\,-3 \right)$ và $B\left( 4;\,1 \right).$ Phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm $A$ thành ${A}',$ biến điểm $B$ thành ${B}'.$ Tính độ dài ${A}'{B}'.$

A.${A}'{B}'=\frac{\sqrt{52}}{2}.$ B.${A}'{B}'=\sqrt{52}.$ C.${A}'{B}'=\frac{\sqrt{50}}{2}.$ D.${A}'{B}'=\sqrt{50}.$

Giải:

Phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm $A$ thành ${A}',$ biến điểm $B$ thành ${B}'$ nên ta luôn có (theo định nghĩa) ${A}'{B}'=\frac{1}{2}AB=\frac{\sqrt{{{\left( 4+2 \right)}^{2}}+{{\left( 1+3 \right)}^{2}}}}{2}=\frac{\sqrt{52}}{2}.$

Chọn A

Câu 7: Trong mặt phẳng tọa độ $Oxy,$ cho hai đường tròn $\left( C \right)$ và $\left( {{C}'} \right)$ có phương trình ${{x}^{2}}+{{y}^{2}}-4y-5=0$ và ${{x}^{2}}+{{y}^{2}}-2x+2y-14=0.$ Gọi $\left( {{C}'} \right)$ là ảnh của $\left( C \right)$ qua phép đồng dạng tỉ số $k,$ khi đó giá trị $k$ là:

A. $k=\frac{4}{3}.$ B.$k=\frac{3}{4}.$ C.$k=\frac{9}{16}.$ D.$k=\frac{16}{9}.$

Giải:

Đường tròn $\left( C \right)$ có bán kính $R=3.$ Đường tròn $\left( {{C}'} \right)$ có bán kính ${R}'=4.$

Suy ra tỉ số đồng dạng $k=\frac{R'}{R}=\frac{4}{3}.$

Chọn A

C. Bài tập tự luyện

Câu 1: Mọi phép dời hình cũng là phép đồng dạng với tỉ số $k$ bằng:

A. $k=1.$ B. $k=-1.$ C. $k=0.$ D. $k=2.$

Câu 2: Mệnh đề nào sau đây là sai?

A. Phép dời hình là phép đồng dạng tỉ số $k=1.$

B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

C. Phép vị tự tỉ số $k$ là phép đồng dạng tỉ số $\left| k \right|.$

D. Phép đồng dạng bảo toàn độ lớn góc.

Câu 3: Mệnh đề nào sau đây là sai?

A. Hai đường thẳng bất kì luôn đồng dạng.

B. Hai đường tròn bất kì luôn đồng dạng.

C. Hai hình vuông bất kì luôn đồng dạng.

D. Hai hình chữ nhật bất kì luôn đồng dạng.

Câu 4: Trong các mệnh đề sau, mệnh đề nào sai?

A. Phép dời hình là phép đồng dạng

B. Phép vị tự là phép đồng dạng

C. Phép đồng dạng là một phép dời hình

D. Có phép vị tự không phải là một phép dời hình

Câu 5: Trong các mệnh đề sau đây mệnh đề nào sai?

A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó

B. Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó

C. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó

D. Phép đối vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó

Câu 6: Trong các mệnh đề sau, mệnh đề nào sai?

A. Có một phép tịnh tiến biến mọi điểm thành chính nó

B. Có một phép đối xứng trục biến mọi điểm thành chính nó

C. Có một phép quay biến mọi điểm thành chính nó

D. Có một phép vị tự biến mọi điểm thành chính nó

Câu 7: Trong mp Oxy, (C)${{(x-2)}^{2}}+{{(y-2)}^{2}}=4$. Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O, tỉ số k=1/2 và phép quay tâm O góc 90^o biến (C) thành đường tròn nào có phương trình sau đây?