Giao Điểm Giữa Đường Thẳng Và Mặt Phẳng

GIAO ĐIỂM ĐƯỜNG THẲNG VÀ MẶT PHẲNG

I. PHƯƠNG PHÁP

II. VÍ DỤ MINH HỌA

Ví dụ 1. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AC và BC . Gọi K là một điểm thuộc cạnh BD ( không trùng với trung điểm). Tìm giao điểm của

a) CD và (MNK)

b) AD và (MNK)

Lời giải.

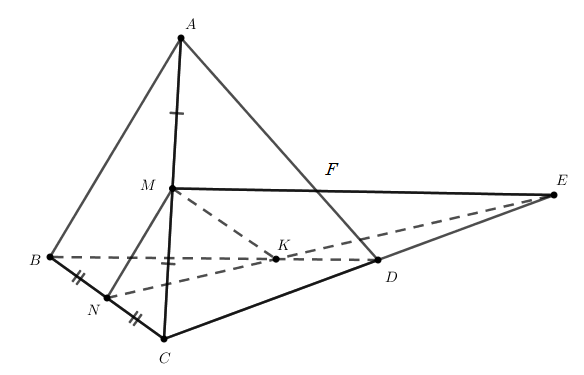
a) Vì K không trùng với trung điểm của BD nên NK không song song với CD.

Gọi $CD\cap NK=\left\{ E \right\}$

Ta có : $E\in NK\subset (MNK)\Rightarrow E\in (MNK)$, mà $E\in CD$(cách dựng)

Khi đó : $CD\cap (MNK)=\left\{ E \right\}$

b) Chọn mặt phẳng phụ chứa AD là mp(ADC). Tìm giao tuyến của 2 mặt phẳng (ADC) và mp(MNK).

Vậy giao điểm của AD với mp(MNK) chính là giao điểm F của AD với đường thẳng ME (như hình vẽ).

Ví dụ 2. Cho hình chóp SABC. Trên SA lấy điểm M , trên SC lấy N , sao cho MN không song song với AC. Gọi O là một điểm nằm trong tam giác ABC . Tìm giao điểm của

a) BC và (OMN)

b) AB và (OMN)

Lời giải.

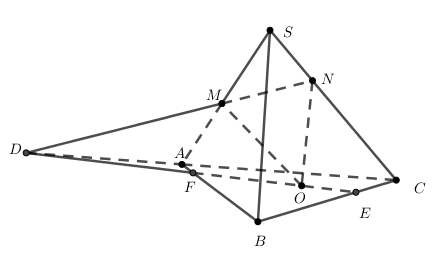
a) Chọn mặt phẳng phụ chứa BC là mp(ABC). Tìm giao tuyến của mp(ABC) và mp(OMN).

Mà O là điểm chung của 2 mặt phẳng (ABC) và (OMN) nên $mp(OMN)\cap mp(ABC)=DO$

Vậy giao điểm của BC và mp(OMN) chính là giao điểm E của BC và DO (như hình vẽ).

b) Chọn mặt phẳng phụ chứa AB là mp(ABC), mà $mp(OMN)\cap mp(ABC)=DO$ nên giao điểm của AB và mp(OMN) chính là giao điểm F của AB và DO (như hình vẽ).

Ví dụ 3. Cho hình chóp SABCD có đáy là tứ giác lồi với các cặp cạnh đối không song song với nhau. Gọi M là một điểm thuộc cạnh SC .

a) Tìm giao điểm của AM và mặt phẳng (SBD)

b) Gọi $N\in BC$ . Tìm giao điểm của SD và (AMN)

Lời giải.

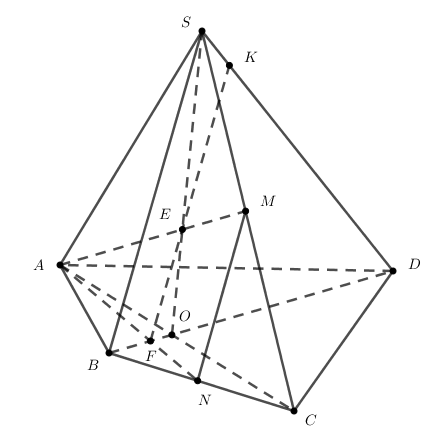
a) Chọn mặt phẳng phụ chứa AM là mp(SAC). Tìm giao tuyến của mp(SAC) và mp(SBD).

Mà $S\in mp(SAC)\cap mp(SBD)$ nên $mp(SAC)\cap mp(SBD)=SO$

Vậy giao điểm của AM và mp(SBD) chính là giao điểm E của AM và SO (như hình vẽ).

b) Chọn mặt phẳng phụ chứa SD là mp(SBD). Tìm giao tuyến của mp(AMN) và mp(SBD).

Mà $E\in mp(AMN)\cap mp(SBD)$ nên $mp(AMN)\cap mp(SBD)=EF$

Vậy giao điểm của SD và mp(AMN) chính là giao điểm K của SD và EF (như hình vẽ).

III. BÀI TẬP TỰ LUYỆN

Bài 1. Cho hình chóp SABCD có đáy là hình bình hành ABCD có tâm O Gọi E là trung điểm của SC

a) Tìm giao tuyến của (BCD) và (SAC)

b) Tìm giao tuyến của (ABE) và (SBD)

c) Tìm giao điểm của SD và (AEB)

Bài 2. Cho hình chóp SABCD có đáy là hình thang với AD là đáy lớn . Gọi E , F là 2 điểm thuộc các cạnh SB và CD.

a) Tìm giao điểm của EF và (SAC)

b) Tìm giao điểm của (AEF) và cạnh BC , SC

Bài 3. Cho tứ diện ABCD . Gọi M, N lần lượt là hai điểm thuộc miền trong của tam giác ABC và BCD . Giả sử MN cắt mặt phẳng (ABD) tại E và cắt (ACD) tại F. Xác định vị trí các điểm E , F.

Bài 4. Cho hình chóp SABCD có AB không song song với CD . Gọi M là điểm thuộc mền trong tam giác SCD.

a) Tìm giao điểm của CD với (MAB)

b) Tìm giao tuyến của (SCD) với (MAB)

c) Tìm giao điểm AM với (SBD)

d) Tìm giao điểm BM với (SAC)

Chúc các bạn học tốt, thân!