Hỗ số, cộng trừ phân số

1. Lý thuyết.

A/ Hỗn số

1. Khái niệm: số gồm phần nguyên và phần phân số. Phần phân số luôn luôn nhỏ hơn 1
2. Muốn viết 1 phân số > 1 dưới dạng hỗn số ta chia tử cho mẫu, thương tìm được là phần nguyên của hỗn số, số dư là tử của phân số kèm theo, còn mẫu vẫn là mẫu đã cho.
3. Muốn viết 1 hỗn số có phần nguyên khác 0 dưới dạng 1 phân số ta nhân phần nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử của phân số, còn mẫu vẫn là mẫu đã cho.

4.   Muốn so sánh hai hỗn số có hai cách:

-  Viết các hỗn số dưới dạng phân số, hỗn số có phân số lớn hơn thì lớn hơn

-  So sánh hai phần nguyên:

+ Hỗn số nào có phần nguyên lớn hơn thì lớn hơn.

+ Nếu hai phần nguyên bằng nhau thì so sánh hai phân số đi kèm, hỗn số có phân số đi kèm lớn hơn thì lớn hơn. Ở bài này ta sử dụng cách hai thì ngắn gọn hơn:

\[4\frac{1}{2}>3\frac{2}{3}\]( do 4 > 3),  \[4\frac{3}{7}>4\frac{3}{8}\] (do \[\frac{3}{7}>\frac{3}{8}\], hai phân số có cùng tử số phân số nsò có mssũ nhỏ hơn thì lớn hơn).

B/ Cộng phân số

1. Cộng 2 phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu số       TQ  a/m  +  b/m   =  (a +b)/m

2. Cộng 2 phân số không cùng mẫu ta quy đồng mẫu số rồi cộng 2 phân số đã quy đồng mẫu số                TQ  a/m  +  b/n   =  (a.n +b.m)/m.n

3. Tính chất:  *   Giao hoán:   a/b  +   c/d    =   c/d   +   a/b

                      *   Kết hợp: (a/b + c/d) + p/q  =  a/b + (c/d + p/q)

                      *   Cộng với 0:  a/b  + 0   =  0  + a/b   =   a/b

                      *   Thêm, bớt vẫn không đổi:   a/b  +  c/d  =  (a/b  + e/f)  +  (c/d  -  e/f)

C/ Trừ phân số

1. Số đối: tổng của chúng bằng 0             *  a/b  +  ( - a/b)   =  0           *  -a/b   =  a/-b   =   -a/b

2. Muốn trừ 1 phân số cho 1 phân số, ta cộng số bị trừ với số đối của số trừ. a/b – c/d  =  a/b + (-c/d)

3. Trừ 2 phân số cùng mẫu ta trừ các tử với nhau và giữ nguyên mẫu số  TQ  a/m - b/m  =  (a -b)/m

4. Trừ 2 phân số không cùng mẫu ta quy đồng mẫu số rồi trừ 2 phân số đã quy đồng mẫu số                TQ  a/m  -  b/n   =  (a.n -b.m)/m.n

5. Khi trừ 2 hỗn số nếu phần phân số của số trừ > phần phân số của số bị trừ thì ta phải rút 1 đơn vị trong phần nguyên của số bị trừ và them vào phần phân số để có 1 phân số > phân số ở số trừ rồi tiếp tục làm như trên.. VD    3. 1/2 – 1.3/4  =  2. 2/3  -  1. 3/4   =  (2-1)   +   (3/2  -  ¾ +   =  1. ¾

6. Tính chất:  Cùng thêm, cùng bớt vẫn không đổi            a/b  -  c/d  =  (a/b  + e/f)  - (c/d  + e/f)

                                                                                                             =  (a/b  - e/f)  - (c/d  - e/f)

     II. Bài tập

Bài 1:  1/ Viết các phân số sau đây dưới dạng hỗn số:           \[\frac{33}{12};\frac{15}{7};\frac{24}{5};\frac{102}{9};\frac{2003}{2002}\]

             2/ Viết các hỗn số sau đây dưới dạng phân số:        \[5\frac{1}{5};9\frac{1}{7};5\frac{2000}{2001};7\frac{2002}{2006};2\frac{2010}{2015}\]

            3/ So sánh các hỗn số sau:             \[3\frac{3}{2}\] và \[4\frac{1}{2}\];   \[4\frac{3}{7}\] và \[4\frac{3}{8}\];                  \[9\frac{3}{5}\] và \[8\frac{6}{7}\]

Hướng dẫn:

1/ \[2\frac{3}{4},2\frac{1}{7},4\frac{4}{5},11\frac{1}{3},1\frac{1}{2002}\]                                2/ \[\frac{76}{15},\frac{244}{27},\frac{12005}{2001},\frac{16023}{2003},\frac{1208}{403}\]

Bài 2:  Tìm 5 phân số có mẫu là 5, lớn hơn 1/5 và nhỏ hơn \[1\frac{2}{5}\].

Hướng dẫn:

\[\frac{1}{5}<\frac{2}{5},\frac{3}{5},\frac{4}{5},\frac{5}{5},\frac{6}{5}<1\frac{2}{5}=\frac{7}{5}\]

Bài 3: Tìm phần nguyên x của hỗn số  x.3/4, biết

a/ x.3/4  =  21989/7996             (x = 2)                b/  2147/425  <  x.3/4  <   2835/420     (  x = 5)

Bài 4: Cho hỗn số 2.x/7. Tìm x biết:

a/ 2.x/7   =  153/63       (x = 3)                           b/  2.7/7 =   (2x + 9)/7                 (x = 5)

Bài 5: Cho hỗn số 11.19/x. Tìm x biết:

a/ 11.19/x   =  1673/140       (x = 20)                           b/  11.19/x =   273/x                 (x = 23)

Bài 6: Cho hỗn số x.2/x. Tìm x biết:

a/ x.2/x   =  12597/1729       (x = 7)                           b/  x.2/x  =   83/x                (x = 9)

Bài 7: Cho hỗn số x.12/13. Tìm x biết:

561/143 < x.12/13  <  1463/247

Bài 8: Tính tổng của các phân số > 1/8  ,  < 1/7  và có tử là 3          (3/22  +  3/23   =  135/506)

Bài 9: Viết mỗi phân số sau đây thành tổng của 2 phân số tối giản có mẫu khác nhau?

a/ 7/15        (1/15  +  6/15  = ……)                      b/  13/27         (1/27 + 12/27  =   ……..)

Bài 10: Dùng 10 chữ số: 0, 1, 2,    ……9 (mỗi chữ số chỉ dùng 1 lần) để lập 2 phân số bằng nhau có tổng bằng 1          ( vô số cách        Ví dụ:    48/96 + 135/270   =  1/2 + 3845/7690  =   …….= 1)

Bài 11: Dùng 10 chữ số: 0, 1, 2,    ……9 (mỗi chữ số chỉ dùng 1 lần) để lập 2 hỗn số có tổng bằng 100.          ( vô số cách        Ví dụ:    78. 3/6   +  21. 45/90   =  71. 3/6   +  28. 45/90  =   …….= 100)

 

Bài 12: Thực hiện phép tính:  9764/36615  +   36.85.20/25.84.34   +   2,2   +    3.19/133

(2,2  =  2.3/15.            kq  =  6.7/15)

Bài 13: Thực hiện phép tính:  1.40404/70707     +   (244.395 – 151)/(244 + 395 .243)  +  

(1.3.5 + 2.6.10 + 4.12.26 + 7.21.35)/(1.5.7 + 2.10.14 + 4.20.28 + 7.35.49)         ( = 3)

Bài 14: Tính

a/ 2/7 + 1/9 + 1/7 + 5/9 + 8/14                                  (1.2/3)

b/ 3/17 + 2.11/34  +  ½                                             (3)

c/ 2/3 + 4/37 + 5/111 + 260/1443                             (1)

d/  5/6  + 4/15  +  6/18  + 3/45            e/ 5/12  +  3/5  +   1/7      f/  3/4 + 4/9  + 25/36 + 13/18  + 1/72

Bài 15: Chứng minh:

a/ 3.17/24 + 2.8/15 + 1.7/8  =  4.3/4  =  3.11/30

b/ 2.4/11  + 5.2/3 + 1.7/11   =   322219/33333

Bài 16: Tính 1 chách hợp lý

a/ 428571/571428  +    30.63.65.8/117.200.49   +   5,25  +   9.578/4046

b/ (1.2.3  + 2.4.6 + 4.8.12 + 7.14.21)/(1.3.5 + 2.6.10 + 4.12.20 + 7.21 .35)  + (74.147 – 73)/(73.147 + 74)   +    216,6

Bài 17: Viết 3/11 thành tổng của 2 phân số có tử số là 1 và mẫu khác nhau?

Bài 18: Viết 5/21 thành tổng của 3 phân số có tử số là 1 và mẫu khác nhau?

Bài 19: Có 5 quả cam chia đều cho 6 người. Làm cách nào để chia được mà không phải cắt bất kỳ quả nào thành 6 phần bằng nhau?

Bài 20:  Cộng các phân số sau:   a/ \[\frac{65}{91}+\frac{-33}{55}\]     b/ \[\frac{36}{-84}+\frac{100}{450}\]        c/ \[\frac{-650}{1430}+\frac{588}{686}\]      d/ \[\frac{2004}{2010}+\frac{8}{-670}\]

Hướng dẫn

             a/ \[\frac{4}{35}\]                   b/ \[\frac{-13}{63}\]                     c/ \[\frac{31}{77}\]                         d/ \[\frac{66}{77}\]

Bài 21: Tìm x biết:       a/ \[x=\frac{7}{25}+\frac{-1}{5}\]                      b/ \[x=\frac{5}{11}+\frac{4}{-9}\]                c/ \[\frac{5}{9}+\frac{x}{-1}=\frac{-1}{3}\]

Hướng dẫn

a/ \[x=\frac{2}{25}\]                      b/ \[x=\frac{1}{99}\]                      c/ \[x=\frac{8}{9}\]

Bài 22:  Cho \[A=\frac{{{10}^{2004}}+1}{{{10}^{2005}}+1}\] và \[B=\frac{{{10}^{2005}}+1}{{{10}^{2006}}+1}\]     So sánh A và B

Hướng dẫn

\[10A=10.\frac{{{10}^{2004}}+1}{{{10}^{2005}}+1}=\frac{{{10}^{2005}}+10}{{{10}^{2005}}+1}=1+\frac{9}{{{10}^{2005}}+1}\]                 \[10B=10.\frac{{{10}^{2005}}+1}{{{10}^{2006}}+1}=\frac{{{10}^{2006}}+10}{{{10}^{2006}}+1}=1+\frac{9}{{{10}^{2006}}+1}\]

Hai phân số có từ số bằng nhau, 10²⁰⁰⁵ +1 < 10²⁰⁰⁶ +1 nên 10A > 10 B              Từ đó suy ra A > B

Bài 23:  Có 9 quả cam chia cho 12 người. Làm cách nào mà không phải cắt bất kỳ quả nào thành 12 phần bằng nhau?

Hướng dẫn

- Lấu 6 quả cam cắt mỗi quả thành 2 phần bằng nhau, mỗi người được ½ quả. Còn lại 3 quả cắt làm 4 phần bằng nhau, mỗi người được ¼ quả. Như vạy 9 quả cam chia đều cho 12 người, mỗi người được \[\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\] (quả).        Chú ý 9 quả cam chia đều cho 12 người thì mỗi người được 9/12 = ¾ quả nên ta có cách chia như trên.

Bài 24:  Tính nhanh giá trị các biểu thức sau:

\[\text{A = }\frac{\text{-7}}{\text{21}}+(1+\frac{1}{3})\]         \[\text{B = }\frac{\text{2}}{\text{15}}+(\frac{5}{9}+\frac{-6}{9})\]                        \[\text{B= (}\frac{\text{-1}}{\text{5}}+\frac{3}{12})+\frac{-3}{4}\]

Hướng dẫn

\[\text{A = (}\frac{\text{-7}}{\text{21}}+\frac{1}{3})+1=0+1=1\]                     \[\text{B = (}\frac{\text{2}}{\text{15}}+\frac{-6}{9})+\frac{5}{9}=\frac{-24}{45}+\frac{25}{45}=\frac{1}{15}\]

\[\text{C= (}\frac{3}{12}+\frac{-3}{4})+\frac{-1}{5}=\frac{-1}{2}+\frac{-1}{5}=\frac{-5}{10}+\frac{-2}{10}=\frac{-7}{10}\]

Bài 25: Tính theo cách hợp lí:

a/ \[\frac{4}{20}+\frac{16}{42}+\frac{6}{15}+\frac{-3}{5}+\frac{2}{21}+\frac{-10}{21}+\frac{3}{20}\]                     b/ \[\frac{42}{46}+\frac{250}{186}+\frac{-2121}{2323}+\frac{-125125}{143143}\]

Hướng dẫn

a/ \[\frac{4}{20}+\frac{16}{42}+\frac{6}{15}+\frac{-3}{5}+\frac{2}{21}+\frac{-10}{21}+\frac{3}{10}\]

 

 

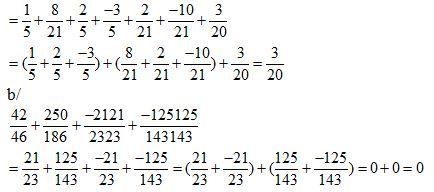
Bài 26:  Tính:

a/ \[\frac{7}{3}+\frac{1}{2}-\frac{-3}{70}\]               b/ \[\frac{5}{12}-\frac{3}{-16}+\frac{3}{4}\]

ĐS:                a/ \[\frac{34}{35}\]                                               b/ \[\frac{65}{48}\]

Bài 27:  Tìm x, biết:

a/ \[\frac{3}{4}-x=1\]                    b/ \[x+4=\frac{1}{5}\]                        c/ \[x-\frac{1}{5}=2\]                   d/ \[x+\frac{5}{3}=\frac{1}{81}\]

ĐS:               a/ \[x=\frac{1}{4}\]                  b/ \[x=-\frac{19}{5}\]                 c/  \[x=\frac{11}{5}\]                           d/ \[x=-\frac{134}{81}\]

Bài 28:  Tính tổng các phân số sau:

a/ \[\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\ldots +\frac{1}{2003.2004}\]                                            b/ \[\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots +\frac{1}{2003.2005}\]

Hướng dẫn

a/ GV hướng dẫn chứng minh công thức sau:             \[\frac{1}{n}-\frac{1}{n+1}=\frac{1}{n(n+1)}\]

HD: Quy đồng mẫu VT, rút gọn được VP.

Từ công thức trên ta thấy, cần phân tích bài toán như sau:

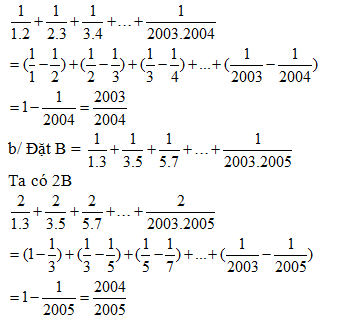
      Suy ra B = \[\frac{1002}{2005}\]

Bài 29:  Hai can đựng 13 lít nước. Nếu bớt ở can thứ nhất 2 lít và thêm vào can thứ hai \[\frac{9}{2}\] lít, thì can thứ nhất nhiều hơn can thứ hai \[\frac{1}{2}\]lít. Hỏi lúc đầu mỗi can đựng được bao nhiêu lít nước?

Hướng dẫn

- Dùng sơ đồ đoạn thẳng để dể dàng thấy cách làm.

- Ta có:        Số nước ở can thứ nhất nhiều hơn can thứ hai là:

\[4\frac{1}{2}+\frac{1}{2}+2=7(l)\]

Số nước ở can thứ hai là (13-7):2 = 3 \[(l)\]

Số nước ở can thứ nhất là 3 +7 = 10 \[(l)\]

Bài 30: Nêu mọi cách viết các phân số sau thành tổng của 2 phân số có tử = 1, mẫu khác nhau.

a/        1/8                            b/   1/10

Hướng dẫn

Gọi 2 phân số cần tìm  1/x,   1/y    (x, y  \[\in \]  N^*).  Ta có:  1/x  +   1/y   =  1/8   (1)

Do x và y có vai trò như nhau nên ta có thể giả sử rằng:   x  <  y.    Từ (1)   =>  1/x  <  1/y  

hay   x   >   8  (2)

Do x  <  y  nên 1/x  >   1/y   =>    1/x  +   1/x   >   1/y  +   1/x        hay   2/x   >   1/8

Do đó  1/x  >  1/16    hay    x< 16 (3)

Từ (2), (3) ta có:    8 < x < 16

Thay x  =  9, 10, 11, 12, 13, 14, 15   vào (1)   =>    x = 9, y = 72;   x = 10, y = 40  ;   x = 12, y = 24

Vậy có tất cả 3 cách viết.         

                                        1/8 = 1/9 + 1/72;              1/8 = 1/10 + 1/40        ;          1/8  =  1/12 + 1/24

b/    1/10  = 1/11 + 1/110 = 1/12 + 1/60   =  1/14 +  1/35  =  1/15  +  1/30

Bài 31: Tính tổng các phân số sau đây 1 cách nhanh chóng nhất.

a/  1/5.6   +  1/6.7  +  1/7.8  +  ….+  1/24.25     b/  2/1.3   +  2/3.5  +  2/5.7  +  ….+  2/99.101   

c/  3/1.3   +  3/3.5  +  3/5.7  +  ….+  3/49.51    d/  1/7   +  1/91  +  1/247  +  1/475 + 1/775 +  1/ 1147   

Hướng dẫn

Ta dễ dàng chứng minh được công thức sau:    a/n.(n +a)   =   1/n   -    1/(n + a). Áp dụng ct trên để tính.

a/   4/25               b/     100/101              c/    1.8/17                       d/     6/37

Bài 32: CMR:\[\forall \] n \[\in \] N  ta có:   1/1.3  +  1/3.5   +  1/5.7  …+  1/(2n + 1).(2n + 3)  =  (n +1)/(2n + 3)

Bài 33: Tính tổng

a/   1/1.2  + 1/2.3  +  1/3.4  +  …+  1/18.19  +  1/19.20

b/  1/20  +  1/30  +   1/42  +  1/56  +  1/72  +   1/90   +  1/110  +   1/132

c/   5²/1.6 + 5²/6.11 + 5²/11.16 + 5²/16.21 + 5²/21.26 + 5²/26.31

Bài 34: Hai vòi nước cùng chảy vào 1 bể. Vòi 1 chảy trong 8h, vòi 2 chảy trong 6h đầy bể. Vòi 3 tháo trong 4h thì bể cạn. Bể đang cạn nếu mở cả 3 vòi thì sau 1h chảy được bao nhiêu phần bể? (1/24 bể)

Bài 35: Tìm số tự nhiên x biết rằng:           1/3  +  1/6  +  1/10  +  …+  2/x.(x + 1)  =   1999/2001

Hướng dẫn

Viết vế trái dưới dạng:  2/2.3  +  2/3.4  +   2/4.5  + ..+  2/x.(x + 1)     =>   x  =   2000

Bài 36: CMR: 1/5 + 1/13 + 1/25 + 1/41 + 1/61 + 1/85 + 1/113  < 1/2

Hướng dẫn

Gọi tổng ở vế trái là S ta có:   S  <  1/5 + (1/12 + 1/12 + 1/12) + (1/60  + 1/60  + 1/60)

                                                S  <  1/5 + (3/12 + 3/60

                                                S  <  1/5 + 1/4 + 1/20     =  (4 + 5 + 1)/20   =  1/20

 

Bài 37: CMR: 1/4 + 1/16 + 1/36 + 1/64 + 1/100 + 1/144 + 1/196   <   1/2. Gỉai bài toán trong trường hợ tổng quát

Hướng dẫn

* 1/4 + 1/16 + 1/36 + 1/64 + 1/100 + 1/144 + 1/196  =  1/2²  + 1/4²  +  1/6² + 1/8²  + 1/10²

         + 1/12²  + 1/14²    =  1/4  +  (1 + 1/2²  + 1/3²  +  1/4² + 1/5²  + 1/6²  + 1/7² )  <  1/4 (1 + 1)  = 1/2

      * Trường hợp tổng quát:  1/2²  +  1/4²  + 1/6²  +…..+  1/(2n)²  <  1/2 .  Tương tự câu trên

Bài 38: CMR:  1/2²  +  1/3²  + 1/4²  +…..+  1/n²  <  1

Hướng dẫn

Vì   1/k² <  1/(k – 1).k    =    1/(k – 1)  -  1/k  nên.

1/2²  +  1/3²  + 1/4²  +…..+  1/n²  <  (1- 1/2) + (1/2 – 1/3)  +  (1/3 – 1/4) +  ….+  [1/(n – 1)  -  1/n]

                                                                                                                                    < 1 – 1/n   <  1

Bài viết gợi ý: