Bài 1: Thực hiện phép nhân sau:
a/ \[\frac{3}{7}\cdot \frac{14}{5}\] b/ \[\]\[\frac{35}{9}\cdot \frac{81}{7}\] c/ \[\frac{28}{17}\cdot \frac{68}{14}\] d/ \[\frac{35}{46}\cdot \frac{23}{205}\]
Hướng dẫn
a/ \[\frac{6}{5}\] b/ \[45\] c/ \[8\] d/ \[\frac{1}{6}\]
Bài 2: Tìm x, biết:
a/ x - \[\frac{10}{3}\] = \[\frac{7}{15}\cdot \frac{3}{5}\] b/ \[x+\frac{3}{22}=\frac{27}{121}\cdot \frac{11}{9}\] c/ \[\frac{8}{23}\cdot \frac{46}{24}-x=\frac{1}{3}\] d/ \[1-x=\frac{49}{65}\cdot \frac{5}{7}\]
Hướng dẫn
a/ x - \[\frac{10}{3}\] = \[\frac{7}{15}\cdot \frac{3}{5}\]
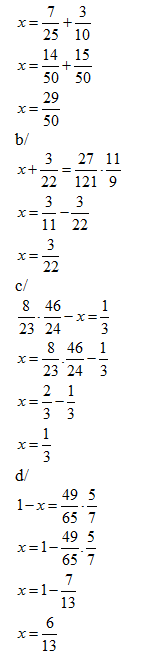
Bài 3: Lớp 6A có 42 HS được chia làm 3 loại: Giỏi, khá, Tb. Biết rằng số HSG bằng 1/6 số HS khá, số HS Tb bằng 1/5 tổng số HS giỏi và khá. Tìm số HS của mỗi loại.
Hướng dẫn
Gọi số HS giỏi là x thì số HS khá là 6x,
số học sinh trung bình là (x + 6x).\[\frac{1}{5}=\frac{x+6x}{5}\]
Mà lớp có 42 học sinh nên ta có: \[x+6x+\frac{7x}{5}=42\]
Từ đó suy ra x = 5 (HS)
Vậy số HS giỏi là 5 học sinh.
Số học sinh khá là 5.6 = 30 (học sinh)
SÁô học sinh trung bình là (5 + 30):5 = 7 (HS)
Bài 4: Tính giá trị của cắc biểu thức sau bằng cach tính nhanh nhất:
a/ \[\frac{21}{25}.\frac{11}{9}.\frac{5}{7}\] b/ \[\frac{5}{23}.\frac{17}{26}+\frac{5}{23}.\frac{9}{26}\] c/ \[\left( \frac{3}{29}-\frac{1}{5} \right)\cdot \frac{29}{3}\]
Hướng dẫn
a/ \[\frac{21}{25}.\frac{11}{9}.\frac{5}{7}=(\frac{21}{25}.\frac{5}{7}).\frac{11}{9}=\frac{11}{15}\] b/ \[\frac{5}{23}.\frac{17}{26}+\frac{5}{23}.\frac{9}{26}=\frac{5}{23}(\frac{17}{26}+\frac{9}{26})=\frac{5}{23}\]
c/ \[\left( \frac{3}{29}-\frac{1}{15} \right)\cdot \frac{29}{3}=\frac{29}{3}.\frac{3}{29}-\frac{29}{45}=1-\frac{29}{45}=\frac{16}{45}\]
Bài 5: Tìm các tích sau:
a/ \[\frac{16}{15}.\frac{-5}{14}.\frac{54}{24}.\frac{56}{21}\] b/ \[\frac{7}{3}.\frac{-5}{2}.\frac{15}{21}.\frac{4}{-5}\]
Hướng dẫn
a/ \[\frac{16}{15}.\frac{-5}{14}.\frac{54}{24}.\frac{56}{21}=\frac{-16}{7}\] b/ \[\frac{7}{3}.\frac{-5}{2}.\frac{15}{21}.\frac{4}{-5}=\frac{10}{3}\]
Bài 6: Tính nhẩm
a/ \[5.\frac{7}{5}\] b. \[\frac{3}{4}.\frac{7}{9}+\frac{1}{4}.\frac{7}{9}\] c/ \[\frac{1}{7}.\frac{5}{9}+\frac{5}{9}.\frac{1}{7}+\frac{5}{9}.\frac{3}{7}\] d/ \[4.11.\frac{3}{4}.\frac{9}{121}\]
Bài 7: Chứng tỏ rằng: \[\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{63}>2\]
Hướng dẫn

Bài 8: Tìm A biết: \[A=\frac{7}{10}+\frac{7}{{{10}^{2}}}+\frac{7}{{{10}^{3}}}+...\]
Hướng dẫn
Ta có (A - \[\frac{7}{10}\]).10 = A. VẬy 10A – 7 = A suy ra 9A = 7 hay A = \[\frac{7}{9}\]
Bài 9: Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A đến B với vận tốc 15 km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ B đến A với vận tốc 12 km/h/ Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Hướng dẫn
Thời gian Việt đi là:
7 giờ 30 phút – 6 giờ 50 phút = 40 phút = \[\frac{2}{3}\] giờ
Quãng đường Việt đi là:
\[15\cdot \frac{2}{3}\]=10 (km)
Thời gian Nam đã đi là:
7 giờ 30 phút – 7 giờ 10 phút = 20 phút = \[\frac{1}{3}\] giờ
Quãng đường Nam đã đi là \[12.\frac{1}{3}=4\] (km)
Bài 10: . Tính giá trị của biểu thức: \[A=\frac{-5x}{21}+\frac{-5y}{21}+\frac{-5z}{21}\] biết x + y = -z
Hướng dẫn
\[A=\frac{-5x}{21}+\frac{-5y}{21}+\frac{-5z}{21}=\frac{-5}{21}(x+y+z)=\frac{-5}{21}(-z+z)=0\]
Bài 11: Tính gí trị các biểu thức A, B, C rồi tìm số nghịch đảo của chúng.
a/ A = \[1-\frac{2002}{2003}\] b/ B = \[\frac{179}{30}-\left( \frac{59}{30}-\frac{3}{5} \right)\] c/ C = \[\left( \frac{46}{5}-\frac{1}{11} \right)\cdot 11\]
Hướng dẫn
a/ A = \[1-\frac{2002}{2003}=\frac{1}{2003}\] nên số nghịch đảo của A là 2003
b/ B = \[\frac{179}{30}-\left( \frac{59}{30}-\frac{3}{5} \right)=\frac{23}{5}\] nên số nghịc đảo cảu B là \[\frac{5}{23}\]
c/ C = \[\left( \frac{46}{5}-\frac{1}{11} \right)\cdot 11=\frac{501}{5}\] nên số nghịch đảo của C là \[\frac{501}{5}\]
Bài 12: Thực hiện phép tính chia sau:
a/ \[\frac{12}{5}:\frac{16}{15}\]; b/ \[\frac{9}{8}:\frac{6}{5}\] c/ \[\frac{7}{5}:\frac{14}{25}\] d/ \[\frac{3}{14}:\frac{6}{7}\]
Bài 13: Tìm x biết:
a/ \[\frac{62}{7}.x=\frac{29}{9}:\frac{3}{56}\] b/ \[\frac{1}{5}:x=\frac{1}{5}+\frac{1}{7}\] c/ \[\frac{1}{2{{a}^{2}}+1}:x=2\]
Hướng dẫn
a/ \[\frac{62}{7}.x=\frac{29}{9}:\frac{3}{56}\Rightarrow x=\frac{5684}{837}\] b/ \[\frac{1}{5}:x=\frac{1}{5}+\frac{1}{7}\Rightarrow x=\frac{7}{2}\]
c/ \[\frac{1}{2{{a}^{2}}+1}:x=2\Rightarrow x=\frac{1}{2(2{{a}^{2}}+1)}\]
Bài 14: Đồng hồ chỉ 6 giờ. Hỏi sau bao lâu kim phút và kim giờ lại gặp nhau?
Hướng dẫn
Lúc 6 giờ hai kim giờ và phút cách nhau 1/ 2 vòng tròn.
Vận tốc của kim phút là: \[\frac{1}{12}\] (vòng/h)
Hiệu vận tốc giữa kim phút và kim giờ là: 1- \[\frac{1}{12}\] = \[\frac{11}{12}\] (vòng/h)
Vậy thời gian hai kim gặp nhau là: \[\frac{1}{2}:\frac{11}{12}\] = \[\frac{6}{11}\] (giờ)
Bài 16: Một canô xuôi dòng từ A đến B mất 2 giờ và ngược dòng từ B về A mất 2 giờ 30 phút. Hỏi một đám bèo trôi từ A đến B mất bao lâu?
Hướng dẫn
Vận tốc xuôi dòng của canô là: \[\frac{AB}{2}\] (km/h)
Vân tốc ngược dòng của canô là: \[\frac{AB}{2,5}\] (km/h)
Vận tốc dòng nước là: \[\left( \frac{AB}{2}-\frac{AB}{2,5} \right)\]: 2 = \[\frac{5AB-4AB}{10}\]: 2 = \[\frac{AB}{20}\] (km/h)
Vận tốc bèo trôi bằng vận tốc dòng nước, nên thời gian bèo trôi từ A đến B là:
AB: \[\frac{AB}{20}\] = AB : \[\frac{20}{AB}\] = 20 (giờ)







