Thực hành dạng toán nhìn hình thực tế
Bài toán thực tế liên quan đến hình học thường xoay quanh một số nội dung như sau: Tính toán để đường đi được ngắn nhất, tính toán để diện tích được lớn nhất, hay cũng có thể đơn giản là tính diện tích hoặc thể tích của một vật…
Bài 1. Người ta xây một bồn chứa nước dạng khối có chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 5 m, 1 m, 2 m. Biết rằng bồn chỉ xây hai vách và mỗi vách có độ dày 10 dm như hình vẽ. Tính xem bồn chưa được bao nhiêu lít nước.
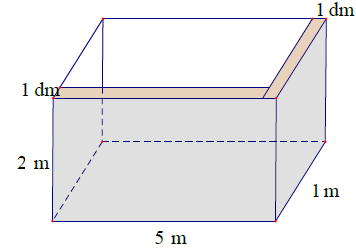
A. 8820 lít. B. 8802 lít. C. 8800 lít. D. 8825 lít.
Bài 2. Cho khối lập phương ABCD.A’B’C’D’ có thể tích bằng 1. Một hình nón có tâm đường tròn đáy trùng với tâm của hình vuông ABCD, đồng thời các điểm A’, B’, C’, D’ nằm trên đường sinh của hình nón. Thể tích nhỏ nhất của khối nón nêu trên là bao nhiêu.
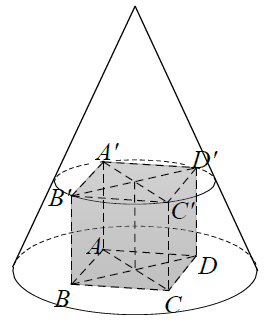
A.$\frac{9}{8}\pi .$ B. $\frac{9}{16}\pi .$ C. $\frac{2}{3}\pi .$ D. Đáp án khác
Bài 3. Từ tấm nhôm hình vuông canh 6 dm. Người ta muốn cắt một hình thang (phần tô đậm trong hình vẽ). Tìm tổng x + y để diện tích hình thang cắt được nhỏ nhất.
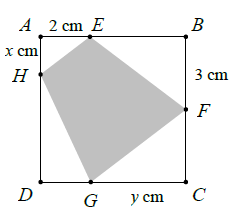
A. 7 B. 5 C.$\frac{7\sqrt{2}}{2}$ D.$4\sqrt{2}$
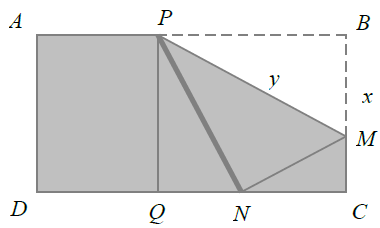
Bài 4. Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiều rộng 8 cm. Gấp góc bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Gọi độ dài nếp gấp là y thì giá trị nhỏ nhất của y là bao nhiêu.
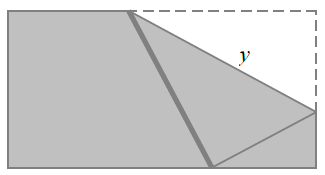
A.$3\sqrt{7}$ B. $3\sqrt{5}$ C. $6\sqrt{3}$ D. $6\sqrt{2}$
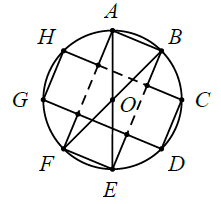
Bài 5. Một miếng bìa hình tròn có bán kính 20 cm. Trên biên của miếng bìa ta xác định 8 điểm A, B, C, D, E, F, G, H theo thứ tự chia đường tròn thành 8 phần bằng nhau. Cắt bỏ theo các nét liền và gấp lại theo các nét đứt tạo thành một cái hộp không nắp. Thể tích của hộp gấp được.
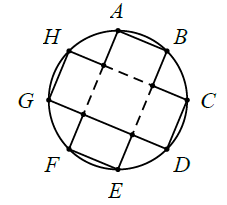
A.$\frac{4000(2-\sqrt{2})\sqrt{4-2\sqrt{2}}}{\sqrt{2}}$ B.$\frac{4000{{(\sqrt{2-\sqrt{2}})}^{3}}}{\sqrt{2}}$
C.$4000(2-\sqrt{2})\sqrt{4-2\sqrt{2}}$ D.$4000{{(\sqrt{2-\sqrt{2}})}^{3}}$
Bài 6. Một chậu nước hình bán cầu bằng nhôm bán kính R = 10cm. Ban đầu lượng nước trong chậu có chiều cao (tính từ đáy chậu đến mặt nước) là h = 4cm, người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên phủ kìn viên bi. Biết rằng thể tích của khối chỏm cầu tính theo công thức$V=\pi {{h}^{2}}\left( R-\frac{h}{3} \right),$ hãy tính bán kính của viên bi (làm tròn đến hàng đơn vị).
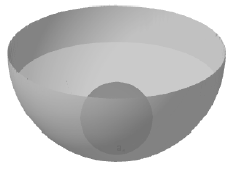
A. 2 cm. B. 4 cm. C. 7 cm. D. 10 cm
Bài 7. Người thợ gốm nặm một cái chum từ một khối đất hình cầu bán kính 5 dm bằng cách cắt bỏ hai chỏm cầu đối diện nhau. Hãy tính thể tích của cái chum biết rằng chiều cao của nó là 60 cm.
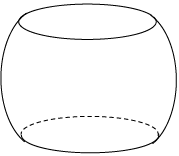
A. 414,48 lít. B. 128,74 lít. C. 104,(6) lít. D. 135,02 lít.
Bài 8. Người ta muốn treo một bóng đèn ở phía trên và chính giữa của một cái bàn có bán kính bằng $\sqrt{2}$ m sao cho mép bàn nhận được nhiều ánh sáng nhất. Biết rằng cường độ sáng C của bóng đèn được biểu thị bởi công thức$C=c\frac{\sin \alpha }{l}$ (trong đó$\alpha $ là góc tạo bởi tia sáng tới mép bàn và mặt bàn, c là hằng số tỉ lệ phụ thuộc vào nguồn sáng, l là khoảng cách từ bóng đèn tới mép bàn). Hỏi phải treo bóng đèn cách mặt bàn bao nhiêu mét.
A. 1 m. B. 1,2 m. C. 1,5 m. D. 2m.
Bài 9. Một miếng bìa hình chữ nhật có chiều dài 50 cm, chiều rộng 20 cm. Người ta chia miếng bìa thành ba phần như hình vẽ để khi gấp lại thu được một hình lăng trụ đứng có chiều cao bằng chiều rộng của miếng bìa. Hỏi diện tích xuang quang của lăng trụ gấp được là bao nhiêu.
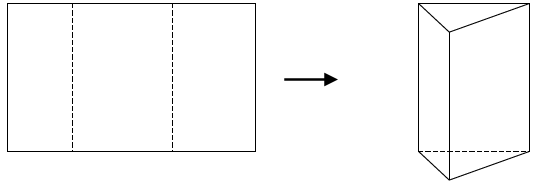
A.$1500c{{m}^{2}}$ B. $2000c{{m}^{2}}$ C. $1000c{{m}^{2}}$ D. $500c{{m}^{2}}$
Bài 10. Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các viên bi đều được tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với 6 viên bi xung quanh và mỗi viên bi xung quanh và mỗi viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Hãy tính diện tích của đáy lọ.
A.$16\pi {{r}^{2}}$ B. $18\pi {{r}^{2}}$ C. $9\pi {{r}^{2}}$ D. $36\pi {{r}^{2}}$
Bài 11. Một gia đình cần xây dựng một hố ga (không nắp) dạng hình hộp chữ nhật có thể tích 3 (m3). Tỉ số giữa chiều cao của hố (h) và chiều rộng của đáy (y) bằng 4. Tìm chiều dài của đáy (x) để tốn ít vật liệu xây hố ga nhất.
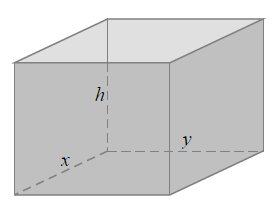
A.$\frac{3}{4}m$ B. 1,5 m C. $\frac{4}{3}m$ D. 2,5 m
Bài 12. Từ một tấm bìa cứng hình vuông cạnh a, người ta cắt bốn góc bốn hình vuông bằng nhau rồi gấp lại tạo thành một hình hộp không nắp. Tìm cạnh của hình vuông bị cắt để thể tích hình hộp lớn nhất.
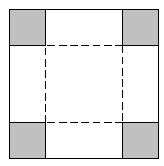
A.$\frac{a}{2}$ B. $\frac{a}{8}$ C. $\frac{a}{3}$ D. $\frac{a}{6}$
Bài 13. Từ tấm nhôm hình vuông cạnh 200 cm, cắt một tấm nhôm hình tam giác vuông có tổng cạnh huyền và một cạnh góc vuông bằng 120 cm. Để miếng nhôm cắt được có diện tích lớn nhất thì cạnh huyền của miếng nhôm đó có độ dài bằng bao nhiêu.
A. 40 cm B.$40\sqrt{3}cm$ C. 80 cm D. $40\sqrt{2}cm$
Bài 14. Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một Kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc bằng nhau MA và NB cao 1,5 mét so với mặt đất. Hai cọc này song song, cách nhau 10 mét và thẳng hàng so với tim cột cờ (xem hình vẽ minh hoạ). Đặt giác kế đứng tại A và B để nhắm đến đỉnh cột cờ, người ta đo được các góc lần lượt là${{51}^{\circ }}40'12''$ và ${{45}^{\circ }}39'$ so với đường song song mặt đất. Hãy tính chiều cao của cột cờ (làm tròn đến 0,01 m).
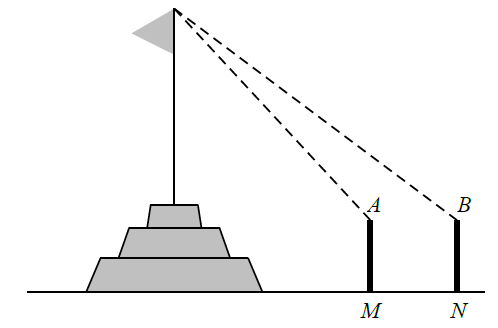
A. 52,20 m. B. 52,29 m. C. 52,30 m. D. 52,31 m.
Bài 15. Người ta muốn làm một con đường từ địa điểm A đến địa điểm B ở hai bên bờ một con sông, các số liệu được thể hiện trên hình vẽ, con đường được làm theo đường gấp khúc AMNB. Biết rằng chi phí xây dựng 1 km đường bên bờ có điểm B gấp 1,3 lần chi phí xây dựng 1 km đường bên bờ có điểm A, chi phí làm cầu MN tại địa điểm nào cũng như nhau. Hỏi phải xây dựng cầu tại điểm M cách điểm H bao nhiêu (làm tròn đến 0,001 km) để chi phí làm đường là nhỏ nhất.
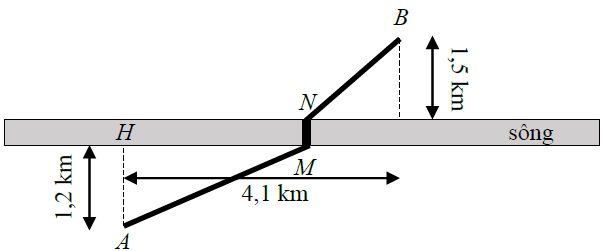
A. 1,758 km. B. 2,630 km. C. 2,360 km. D. Kết quả khác.
Hướng dẫn giải:
Bài 1.$V=50.20.10-10.20.1-49.20.1=8820$ (lít)
Bài 2.
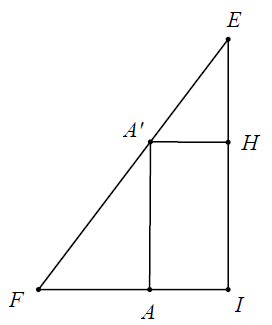
Gọi I là tâm hình vuông ABCD, H là tâm của hình vuông A’B’C’D’, EF là đường sinh đi qua như hình vẽ bên.
Do hình lập phương có thể tích bằng 1 nên ta có:\[\text{AA}'=HI=1,A'H=AI=\frac{\sqrt{2}}{2}.\]
Đặt EH = x ta có: $\frac{x}{EI}=\frac{A'H}{FI}\Leftrightarrow \frac{x}{x+1}=\frac{\sqrt{2}}{2FI}\Leftrightarrow FI=\frac{\sqrt{2}}{2}\left( \frac{x+1}{x} \right)(=r).$
Thể tích khối nón là:$\frac{1}{3}\pi {{r}^{2}}EI=\frac{1}{6}\pi {{\left( \frac{x+1}{x} \right)}^{2}}(x+1)=\frac{\pi }{6}.\frac{{{(x+1)}^{3}}}{{{x}^{2}}}$
Xét hàm số$f(x)=\frac{{{(x+1)}^{3}}}{{{x}^{2}}}$ trong đó x > 0 ta có$f'(x)=\frac{(x-2){{(x+1)}^{2}}}{{{x}^{3}}}$ . Do đó thể tích khối nón đạt giá trị nhỏ nhất khi và chỉ khi x = 2. Thể tích khối nón khi đó là: $\frac{9\pi }{8}$
Bài 3. Diện tích hình thang nhỏ nhất khi $S={{S}_{AEH}}+{{S}_{CGF}}+{{S}_{DGH}}$ lớn nhất.
Ta có:$2S=2x+3y+(6-x)(6-y)=xy-4x-3y+36$ (1)
Mà hai tam giác AEH và CGF đồng dạng nên$\frac{AE}{CG}=\frac{AH}{CF}=>xy=6$ (2)
Thay (2) vào (1) ta có:$2S=42-\left( 4x+\frac{18}{x} \right)$ 2S lớn nhất khi $4x+\frac{18}{x}$ nhỏ nhất
Suy ra:$4x=\frac{18}{x}=>x=\frac{3\sqrt{2}}{2}=>y=2\sqrt{2}=>x+y=\frac{7\sqrt{2}}{2}.$
Bài 4.
.png)
Bài 5.
.png)
.png)
Bài 7. Chọn hệ trục toạ độ Oxy như hình vẽ.
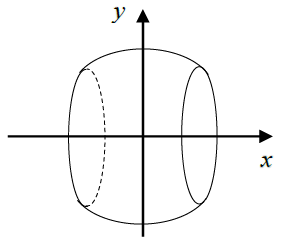
Thể tích của cái chum là thể tích của hình giới hạn bởi đường tròn có phương trình $y=\sqrt{25-{{x}^{2}}}$ và các đường thẳng$x=\pm 3$ khi quay xung quanh trục Ox.
Suy ra:$V=\pi \int\limits_{-3}^{3}{(25-{{x}^{2}})dx=132\pi .}$
Bài 8. Gọi h là khoảng cách từ bóng đèn đến mặt bàn.
Ta có :$\sin \alpha =\frac{h}{l}$ và ${{h}^{2}}={{l}^{2}}-2.$
Suy ra cường độ sáng ở mép bàn là:$C=C(h)=c\frac{h}{{{l}^{3}}}=\frac{ch}{{{\left( \sqrt{{{h}^{2}}+2} \right)}^{3}}}$
Ta có:$C(1)=\frac{c}{{{(\sqrt{3})}^{3}}};C(1,2)=\frac{1,2c}{{{(\sqrt{3,44})}^{3}}};C(1,5)=\frac{1,5c}{{{(\sqrt{4,25})}^{3}}};C(2)=\frac{2c}{{{(\sqrt{6})}^{3}}}$
Suy ra h = 1 m thì cường độ sáng ở mép bàn là lớn nhất.
Bài 9. HD: Diện tích xung quanh của cái hộp bằng diện tích của miếng bìa.
Bài 10. Bán kính của đáy lọ là:$R=r+2r=3r.$
Diện tích của đáy lọ là:$s=\pi {{R}^{2}}=\pi {{(3r)}^{2}}=9\pi {{r}^{2}}$
Bài 11. Ta có:$\frac{h}{y}=4=>h=4y$
Do thể tích của hố ga là nên ta có:$xyh=3=>xy4y=3\Leftrightarrow x=\frac{3}{4{{y}^{2}}}$
Tổng diện tích của các mặt cần xây là:
$xy+2xh+2yh=\frac{3}{4{{y}^{2}}}.y+2.\frac{3}{4{{y}^{2}}}.4y+2y.4y=\frac{3}{4y}+\frac{6}{y}+8{{y}^{2}}=8{{y}^{2}}+\frac{27}{4y}$
Ta có:$8{{y}^{2}}+\frac{27}{4y}=8{{y}^{2}}+\frac{27}{8y}+\frac{27}{8y}\overset{AM-GM}{\mathop{\ge }}\,3\sqrt[3]{8{{y}^{2}}.\frac{27}{8y}.\frac{27}{8y}}=\frac{9}{2}.$
Đẳng thức xảy ra khi:$8{{y}^{2}}=\frac{27}{8y}\Leftrightarrow y=\frac{3}{4}=>x=\frac{4}{3}$
Bài 12. Gọi x là độ dài của cạnh của bốn hình vuông cắt bỏ$(0
Thể tích của cái hộp là:$V=(a-2x)(a-2x)x=\frac{1}{4}\left[ (a-2x)(a-2x).4x \right]\overset{AM-GM}{\mathop{\le }}\,\frac{1}{4}{{\left( \frac{a-2a+a-2x+4x}{3} \right)}^{3}}=\frac{2{{a}^{3}}}{27}.$
Đẳng thức xảy ra khi:$a-2x=4x\Leftrightarrow x=\frac{a}{6}.$
Bài 13. Gọi x là độ dài một cạnh góc vuông ( x > 0 ),thì độ dài cạnh huyền là 120 - x và độ dài cạnh góc vuông còn lại là $\sqrt{14400-240x}.$
Diện tích của miếng nhôm cắt được là:$f(x)=\frac{1}{2}x\sqrt{14400-240x}$
Ta có:$f(x)=\frac{1}{2}\sqrt{{{x}^{2}}(14400-240x)}=\frac{1}{2.120}\sqrt{120x.120x.(14400-240x)}$
Suy ra f(x) lớn nhất khi $120x=14400-240x\Leftrightarrow x=40$ do đó cạnh huyền bằng 80 cm thì diện tích của miếng nhôm là lớn nhất.
Bài 14.
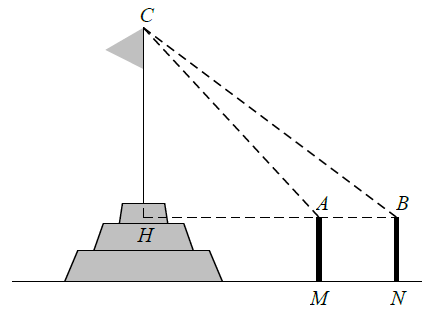
Gọi H là giao điểm của AB với tim cột cờ. Ta cần tính chiều cao của cột cờ tức là tính HC.
Xét tam giác ABC ta có:$C=A-B={{6}^{0}}{{10}^{'}}{{12}^{''}}$
Theo định lý hàm sin trong tam giác ABC ta có:$\frac{AB}{\sin C}=\frac{AC}{\sin B}=>AC=\frac{10.\sin {{45}^{0}}{{39}^{'}}}{\sin {{6}^{0}}{{10}^{'}}{{12}^{''}}}$
Ta có:$HC=AC.\sin CAH=AC.\sin {{51}^{0}}{{49}^{'}}{{12}^{''}}$
$\Leftrightarrow HC=\frac{10\sin {{45}^{0}}{{39}^{'}}\sin {{51}^{0}}{{49}^{'}}{{12}^{''}}}{\sin {{6}^{0}}{{10}^{'}}{{12}^{''}}}\approx 52,30(m).$
Bài 15. Đặt$HM=x,(0\le x\le 4,1).$ Suy ra :$AM=\sqrt{{{x}^{2}}+1,44},BN=\sqrt{{{(4,1-x)}^{2}}+2,25}.$
Gọi a là số tiền để làm 1 km đường bên bờ có điểm A. Không mất tính tổng quát giả sử a = 1 thì số tiền để làm đường là: $f(x)=1.\sqrt{{{x}^{2}}+1,44}+1,3.\sqrt{{{(4,1-x)}^{2}}+2,25}$
Ta có:$f'(x)=\frac{x}{\sqrt{{{x}^{2}}+1,44}}+1,3.\frac{4,1-x}{\sqrt{{{(4,1-x)}^{2}}+2,25}}$
Sử dụng MTCT ta tính được$f'(x)=0$ khi $x\approx 2,630356850={{x}_{0}}$.
Suy ra: HM = 2,630 (km).







