[TOÁN 12] Quy Tắc Đếm

QUY TẮC ĐẾM

A/ LÝ THUYẾT

I/ Quy tắc cộng

1/ Khái niệm

+ Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất cứ cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

+ Quy tắc cộng thực chất là quy tắc đến số phần tử của tập hợp hai tập hợp hữu hạn không giao nhau: Nếu A và B là hai tập hợp hữu hạn không giao nhau thì:

$m(A\cup B)=m(A)+m(B)$

+ Quy tắc có thể mở rộng cho nhiều hành động hay nhiều tập hợp.

2/ Ví dụ

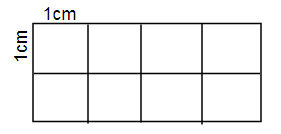
VD1: Có bao nhiêu hình vuông trong hình sau:

A.8

B.3

C.5

D.11

Giải:

Ta thấy có 2 loại hình vuông là: Hình vuông cạnh 1cm (tập hợp A) và Hình vuông cạnh 2cm (tập hợp B) và 2 tập hợp này không giao nhau.

m(A) = số hình vuông cạnh 1 cm = 4 x 2 = 8 (hình)

m(B) = số hình vuông cạnh 2 cm = 3 (hình)

Vậy số hình vuông có trong hình trên là 8 + 3 = 11 (hình)

Đáp án D

VD 2: Có bao nhiêu số tự nhiên có hai chữ số mà chữ số hàng đơn vị nhỏ hơn chữ số hàng chục?

A.9

B.36

C.45

D.64

Giải:

Nếu chữ số hàng chục là n thì số có chữ số hàng đơn vị là n – 1 thì số các chữ số nhỏ hơn n nằm ở hàng đơn vị cũng bằng n

Do chữ số hàng chục lớn hơn hoặc bằng 1 còn chữ số hàng đơn vị thì lớn hơn hoặc bằng 0

Vấy số các số cần tìm là:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 (số ).

Đáp án C

II/ Quy tắc nhân

1/ Khái niệm

Một công việc phải được hoàn thành bởi hai hành động liên tiếp nhau. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì ta có m.n cách hoàn thành công việc

2/ Ví dụ

VD 1: Bạn An có 3 cái mũ màu khác nhau, 4 cái áo màu khác nhau, 2 cái quần màu khác nhau, 2 đôi giày màu khác nhau. Hỏi bạn An có bao nhiêu cách chọn ra 1 bộ?

A.11

B.48

C.12

D.4

Giải:

Để được 1 bộ thì phải thực hiện 4 hành động liên tiếp

+ Chọn mũ: có 3 cách chọn.

+ Chọn áo: có 4 cách chọn.

+ Chọn quần: có 2 cách chọn.

+ Chọn giày: có 2 cách chọn.

Vậy số cách chọn ra một bộ là: 3.4.2.2 = 48 (cách).

Đáp án B

VD2:

a/ Có bao nhiêu số điện thoại có 11 chữ số

A.${{10}^{11}}$

B.${{10}^{10}}$

C.${{9}^{11}}$

D.${{9}^{10}}$

Giải:

Một số điện thoại có 11 chữ số (11 vị trí):

+ Có thể chọn 10 chữ số đơn vị cho vị trí thứ nhất

+ Với mỗi cách chọn ở vị trí thứ nhất thì có 10 cách chọn cho vị trí thứ hai

+ …

+ Cuối cùng, với mỗi cách chọn 10 vị trí đầu ta lại có 10 cách chọn cho vị trí cuối cùng

Vậy số cách chọn là ${{10}^{11}}$ (cách chọn) tương ứng với ${{10}^{11}}$ (số điện thoại).

Đáp án A

b/ Nếu có 1 tỉ người dùng điện thoại, mỗi người sở hữu một số thì số điện thoại phải có ít nhất bao nhiêu chữ số?

A.8

B.9

C.10

D.11

Giải:

Với 1 tỉ người và mỗi người sử dụng một số điện thoại thì có 1000000000 số

Để có 1000000000 số thì số điện thoại phải có ít nhất 9 chữ số.

Đáp án B

III/ Các bài toán đếm cơ bản

*Bài toán 1: Đếm số phương án liên quan đến số tự nhiên

Khi lập một số tự nhiên $x=\overline{{{a}_{1}}{{a}_{2}}{{a}_{3}}...{{a}_{n-1}}{{a}_{n}}}$ cần lưu ý:

+ ${{a}_{i}}\in \left\{ 0;1;2;...;9 \right\}$ và ${{a}_{1}}\ne 0$

+ x là số chẵn khi ${{a}_{n}}\in \left\{ 0;2;4;6;8 \right\}$

+ x là số lẻ khi ${{a}_{n}}\in \left\{ 1;3;5;7;9 \right\}$

+ x chia hết cho 3 khi ${{a}_{1}}+{{a}_{2}}+...+{{a}_{n}}$ chia hết cho 3

+ x chia hết cho 4 khi $\overline{{{a}_{n-1}}{{a}_{n}}}$ chia hết cho 4

+ x chia hết cho 5 khi ${{a}_{n}}\in \left\{ 0;5 \right\}$

+ x chia hết cho 6 khi x là số chẵn và chia hết cho 3

+ x chia hết cho 8 khi $\overline{{{a}_{n-2}}{{a}_{n-1}}{{a}_{n}}}$ chia hết cho 8

+ x chia hết cho 9 khi ${{a}_{1}}+{{a}_{2}}+...+{{a}_{n}}$ chia hết cho 9

+ x chia hết cho 11 khi tổng cách chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số chia hết cho 11

+ x chia hết cho 25 khi $\overline{{{a}_{n-1}}{{a}_{n}}}\in \left\{ 00;25;50;75 \right\}$

*Bài toán 2: Đếm số phương án liên quan đến kiến thực tế

*Bài toán 3: Đếm số phương án liên quan đến hình học

B/ BÀI TẬP

Câu 1: Từ các chữ số 0;2;4;6;8 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau?

A.60

B.40

C.48

D.10

Câu 2: Từ các chữ số 1;2;3;4;5;6;7 có bao nhiêu số có 5 chữ số sao cho chữ số đầu tiên bằng 3?

A.16807

B.5040

C.240

D.2401

Câu 3: Từ các chữ số 1;2;3 có thể lập được bao nhiêu số các 3 chữ số?

A.6

B.8

C.12

D.27

Câu 4: Có bao nhiêu số có hai chữ số mà các chữ số đều lẻ?

A.25

B.20

C.30

D.10

Câu 5: Có bao nhiêu số tự nhiên gồm 5 chữ số lớn hơn 4 và đôi một khác nhau?

A.240

B.120

C.360

D.24

Câu 6: Từ các chữ số 0;1;2;3;4;5;6 có thể lập được bao nhiêu số lẻ có 4 chữ số?

A.720

B.261

C.235

D.679

Câu 7: Tính tổng các số có 5 chứ số được lập từ các số 1;2;3;4;5?

A.5599944

B.33778933

C.4859473

D.3847294

Câu 8: Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 6?

A.12

B.16

C.17

D.20

Câu 9: Số các số tự nhiên có 5 chữ số chia hết cho 10?

A.3260

B.3168

C.9000

D.12070

Câu 10: Có tất cả bao nhiê số tự nhiên có 2018 chữ số chia hết cho 9 và trong đó có ít nhát hai chữ số 9?

A.$\frac{{{9}^{2018}}-{{2019.9}^{2017}}+8}{9}$

B.$\frac{{{9}^{2018}}-{{2.9}^{2017}}+8}{9}$

C.$\frac{{{9}^{2018}}-{{9}^{2017}}+8}{9}$

D.$\frac{{{9}^{2018}}-{{19.9}^{2017}}+8}{9}$

Câu 11: Từ thành phố A đến thành phố B có 6 con đường, từ thành phố B đến thành phố C có 7 con đường. Hỏi từ thành số A đến thành phố C có bao nhiêu cách?

A.6

B.7

C.13

D.42

Câu 12: Trong một giải thi đấu có 20 đội tham gia với thể thức thi đấu vòng tròn. Cứ hai đội thì gặp nhau đúng một lần. Hỏi có bao nhiêu trận đấu xảy ra?

A.190

B.182

C.280

D.194

Câu 13: Có 10 cặp vợ chống đi dự tiệc. Tổng số cách chọn ra một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho 2 người đó không là vợ chồng?

A.100

B.91

C.10

D.90

Câu 14: Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh vào một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?

A.6

B.72

C.720

D.144

Câu 15: Số điện thoại ở huyện Lệ Thủy có 7 chữ số và bắt đầu bởi 3 chữ số đầu tiên là 210. Hỏi ở huyện Lệ Thủy có tối đa bao nhiêu số điện thoại?

A.1000

B.100000