Tổng hợp dao động

A.KIẾN THỨC:

1. Tổng hợp hai dao động điều hoà cùng phương cùng tần số như sau:

x₁ = A₁cos (wt + j₁)  và x₂ = A₂cos (wt + j₂)  thì:  x = x₁ + x₂  thì ta được  x = Acos (wt + j) . Với:

 A²=A₁²+ A₂²+2A₁A₂cos (j₂ - j₁);   j: tan j = $\frac{A1sin\varphi 1+ A2sin\varphi 2}{A1cos\varphi 1+ A2cos \varphi 2}$          với j₁  ≤ j  ≤ j₂  (nếu j₁ ≤ j₂ )

2.Nếu một vật tham gia đồng thời nhiều dao động điều hoà cùng phương cùng tần số:

 x₁ = A₁cos (wt + j₁), x₂ = A₂cos (wt + j₂) và x₃ = A₃cos (wt + j₃) ... thì dao động tổng hợp cũng là dao động điều hoà cùng phương cùng tần số: x = Acos (wt + j) . 

Chiếu lên trục Ox và trục Oy trong hệ xOy. Ta được:      A_x = Acos j = A₁cos j₁+  A₂cos j₂+   A₃cos j₃ +     ..

                                                                            và A_y = A sin j = A₁sin j₁+    A₂sin j₂+   A₃sin j₃ +     ..

Biên độ: :  A = \[\sqrt{A_{x}^{2}+A_{y}^{2}}\] và  Pha ban đầu j : tan j = \[\frac{{{A}_{y}}}{{{A}_{x}}}\]   với  j Π [j _Min, j _Max]

   3.Khi biết dao động thành phần x₁=A₁cos (wt + j₁)  và dao động tổng hợp x = Acos(wt + j)   thì dao động thành phần còn lại là x₂ =x - x_{1  .}   với  x₂ = A₂cos (wt + j₂) .

Biên độ: A₂²=A²+ A₁²-2A₁Acos(j -j₁); Pha tan j₂=\[\frac{A\sin \varphi -{{A}_{1}}\sin {{\varphi }_{1}}}{A\cos \varphi -{{A}_{1}}\cos {{\varphi }_{1}}}\]với j₁≤ j ≤ j₂ (nếu j₁≤ j₂)

4.Nhược điểm của phương pháp trên khi làm trắc nghiệm:

-Xác định A và j  của dao động tổng hợp theo phương pháp trên mất nhiều thời gian và dễ nhầm lẫn.Việc biểu diễn giản đồ véctơ, đôi khi khó biểu diễn được với những bài toán tổng hợp từ 3 dao động trở lên.

-Xác định góc j hay j₂   thật sự khó khăn đối với học sinh bởi vì cùng một giá trị tanj  luôn tồn tại hai giá trị của j (ví dụ: tanj=1 thì j = p/4 hoặc -3p/4), vậy chọn giá trị nào cho phù hợp với bài toán!.

B. PHƯƠNG PHÁP: Dùng máy tính CASIO fx – 570ES, 570ES Plus hoặc CASIO fx – 570MS.

   1. Cơ sở lý thuyết:

+Dao động điều hoà  x = Acos(wt + j)  có thể được biểu diễn bằng vectơ quay \[\overrightarrow{A}\] có độ dài tỉ lệ với biên độ A và tạo với trục hoành một góc bằng góc pha ban đầu j. Hoặc cũng có thể biểu diễn bằng số phức dưới dạng: z = a + bi

+Trong tọa độ cực: z =A(sinj +i cosj)  (với môđun: A= \[\sqrt{{{a}^{2}}+{{b}^{2}}}\])  hay Z = Ae^{j(wt + j).}

+Vì các dao động có cùng tần số góc w  nên  thường viết quy ước z = Ae^Jj, trong máy tính CASIO fx- 570ES  kí hiệu dưới dạng là:  r Ð q   (ta hiểu là: A Ð j).

+Đặc biệt giác số j trong phạm vi : -180⁰<  j < 180⁰  hay -p<j < p rất phù hợp với bài toán tổng hợp dao động trên. Vậy tổng hợp các dao động điều hoà cùng phương, cùng tần số bằng phương pháp Frexnen đồng nghĩa với việc cộng các số phức biểu diễn của các dao động đó.

   2.Chọn chế độ thực hiện  phép tính về số phức  của máy tính: CASIO fx – 570ES, 570ES Plus

         

Ví dụ: Cách nhập: Máy tính CASIO fx – 570ES

  Cho: x= 8cos(wt+ p/3) sẽ được biểu diễn với số phức 8Ð 60⁰ hay 8Ðp/3 ta làm như sau:

 -Chọn mode: Bấm máy: MODE  2  màn hình xuất hiện chữ CMPLX

   

3.Lưu ý :Khi thực hiện phép tính kết quả được hiển thị dạng đại số: a +bi (hoặc dạng cực: AÐ j ).

   -Chuyển từ dạng : a + bi sang dạng:  AÐ j , bấm SHIFT 2 3 =

       Ví dụ: Nhập: 8 SHIFT (-) (p:3) ->Nếu hiển thị: 4+ $4\sqrt{3}$i .Ta bấm phím  SHIFT 2 3 =   kết quả: 8Ð\[\frac{1}{3}\pi \]

   -Chuyển từ dạng  AÐ j sang dạng : a + bi : bấm SHIFT 2 4 =

      Ví dụ: Nhập: 8 SHIFT (-) (p:3)  -> Nếu hiển thị: 8Ð\[\frac{1}{3}\pi \], ta bấm phím  SHIFT 2 4 =  kết quả  :4+$4\sqrt{3}$

          

   4. Tìm dao động tổng hợp xác định A và  j  bằng cách dùng máy tính thực hiện phép  cộng:

   a.Với máy FX570ES: Bấm  MODE 2   màn hình xuất hiện chữ: CMPLX.

    -Chọn đơn vị đo góc là độ bấm:  SHIFT MODE 3  màn hình hiển thị chữ D

  (hoặc Chọn đơn vị góc là Rad bấm: SHIFT MODE 4 màn hình hiển thị chữ R )

 -Nhập A₁  SHIFT (-)  φ_1,  + Nhập A₂  SHIFT (-)  φ₂   nhấn = hiển thị kết quả......

  (Nếu hiển thị  số phức dạng: a+bi  thì bấm SHIFT 2  3  =  hiển thị kết quả: AÐj)

    b.Với máy FX570MS : Bấm chọn MODE 2  màn hình xuất hiện chữ: CMPLX.

    Nhập A₁ SHIFT (-)  φ₁  +   Nhập A₂  SHIFT (-)  φ₂    = 

    Sau đó bấm SHIFT  +  =  hiển thị kết quả là: A. SHIFT   =   hiển thị kết quả là:  φ

    c.Lưu ý Chế độ hiển thị màn hình kết quả:

     Sau khi nhập ta ấn dấu =  có thể hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta  ấn SHIFT         =   (hoặc dùng phím SóD  )  để chuyển đổi kết quả Hiển thị.

d.Các ví dụ:

Ví dụ 1: Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có phương trình: x₁ = 5cos(\[\pi \]t +\[\pi \]/3) (cm); x₂ = 5cos\[\pi \]t (cm). Dao động tổng hợp của vật có phương trình

    A.  x = 5\[\sqrt{3}\]cos(\[\pi \]t -\[\pi \]/4 ) (cm)                 B.x = 5\[\sqrt{3}\]cos(\[\pi \]t + \[\pi \]/6) (cm)

    C.  x = 5cos(\[\pi \]t + \[\pi \]/4) (cm)                                  D.x = 5cos(\[\pi \]t - \[\pi \]/3) (cm)   

      

Giải 2: Dùng đơn vị đo góc là Rad (R): SHIFT MODE  4

  Bấm  MODE 2  màn hình xuất hiện: CMPLX. Tìm dao động tổng hợp:

 Nhập: 5 SHIFT  (-).Ð (p/3) + 5 SHIFT  (-) Ð 0 =  Hiển thị: 5\[\sqrt{3}\]Ð\[\frac{1}{6}\pi \]Hay: x = 5\[\sqrt{3}\]cos(\[\pi \]t + \[\pi \]/6) (cm)

Ví dụ 2: Một vật thực hiện đồng thời 2 dao động điều hoà cùng phương, cùng tần số có phương trình: x₁ = $\sqrt{3}$cos(ωt + p/2) cm, x₂ = cos(ωt + p) cm. Phương trình dao động tổng hợp:

A. x = 2cos(ωt - p/3) cm       B. x = 2cos(ωt + 2p/3)cm        C. x = 2cos(ωt + 5p/6) cm           D. x = 2cos(ωt - p/6) cm

 

Cách 2: Dùng máy tính:Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện chữ: CMPLX

 Chọn chế độ máy tính  theo độ: SHIFT MODE  3

 Tìm dao động tổng hợp: Nhập máy:$\sqrt{3}$ SHIFT  (-).Ð (90) +  1 SHIFT  (-). Ð 180 = Hiển thị:2Ð120

Ví dụ 3:  Một vật thực hiện đồng thời 2 dao động điều hoà cùng phương, cùng tần số có phương trình:x₁ = $\sqrt{3}$cos(ωt - p/2) cm, x₂ = cos(ωt) cm. Phương trình dao động tổng hợp:

A. x = 2cos(ωt - p/3) cm   B.x = 2cos(ωt + 2p/3)cm    C.x = 2cos(ωt + 5p/6) cm    D.x = 2cos(ωt - p/6) cm

         

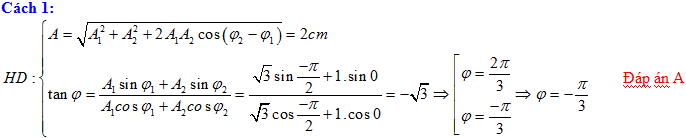
Cách 2: Dùng máy tính:Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện chữ: CMPLX

Chọn chế độ máy tính theo radian(R): SHIFT MODE  4

 Tìm dao động tổng hợp: Nhập máy:$\sqrt{3}$SHIFT  (-).Ð (-p/2) + 1 SHIFT  (-) Ð 0 = Hiển thị:2Ð-p/3

Ví dụ 4: Một vật đồng thời tham gia 3 dao động cùng phương có phương trình dao động: x₁= 2\[\sqrt[{}]{3}\]cos(2πt +\[\frac{\pi }{3}\]) cm, x₂ = 4cos (2πt +\[\frac{\pi }{6}\]) cm ;x₃= 8cos (2πt -\[\frac{\pi }{2}\]) cm. Giá trị vận tốc cực đại của vật và pha ban đầu của dao động lần lượt là:

A. 12πcm/s và \[-\frac{\pi }{6}\]rad .                                                        B. 12πcm/s và \[\frac{\pi }{3}\]rad.     

C. 16πcm/s và\[\frac{\pi }{6}\] rad.                                                           D. 16πcm/s và \[-\frac{\pi }{6}\]rad

 

Cách 2: Với máy FX570ES: Bấm:   MODE 2  ;Đơn vị đo góc là độ (D)bấm: SHIFT MODE 3  

Nhập: 2$\sqrt{3}$ Ø  SHIFT  (-)Ð 60 +  4 SHIFT  (-) Ð 30  +   8 SHIFT  (-) Ð -90  = Hiển thị kết quả:  6Ð-30

( Nếu hiển thị dạng : 3$\sqrt{3}$ -3i  thì bấm SHIFT 2 3 =  Hiển thị: 6 Ð-30 ) => vmax= Aw =12p (cm/s) ; j=p/6

Ví dụ 5: Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số

x₁= cos(2pt + p)(cm), x₂ = $\sqrt{3}$cos(2pt - p/2)(cm). Phương trình của dao động tổng hợp

  A. x = 2.cos(2pt - 2p/3) (cm)                        B. x = 4.cos(2pt + p/3) (cm)

  C. x = 2.cos(2pt + p/3) (cm)                         D. x = 4.cos(2pt + 4p/3) (cm)            

  Giải: Với máy FX570ES : Bấm  MODE 2   màn hình xuất hiện chữ: CMPLX

          Chọn đơn vị đo góc là rad (R):  SHIFT MODE  4

         -Nhập máy: 1 SHIFT(-) Ð p + $\sqrt{3}$SHIFT(-) Р-$\frac{\pi }{2}$= Hiển thị  2Ð-$\frac{2\pi }{3}$ .     Đáp án A

Giải 1: Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện chữ: CMPLX

             Chọn đơn vị đo góc là radian(R): SHIFT MODE  4

             

Ví dụ 7: Ba dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là x₁= 4 cos(pt - p/2) (cm) , x₂= 6cos(pt +p/2) (cm) và x₃=2cos(pt) (cm). Dao động tổng hợp của 3 dao động này có biên độ và pha ban đầu là

A. 2\[\sqrt{2}\]cm;  p/4 rad         B. 2\[\sqrt{3}\]cm; - p/4  rad                C.12cm; + p/2  rad          D.8cm; - p/2  rad

   Giải: Với máy FX570ES : Bấm chọn MODE 2   màn hình xuất hiện chữ: CMPLX

    Chọn đơn vị góc tính rad (R). SHIFT MODE  4 Tìm dao động tổng hợp, nhập máy:

   4 SHIFT(-)Ð (- p/2) + 6 SHIFT(-)Ð (p/2) + 2 SHIFT(-)Ð 0  =   Hiển thị: $2\sqrt{2}$Ð p/4.  Chọn A

Ví dụ 8:  Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số

 x₁= a$\sqrt{2}$cos(pt+p/4)(cm) và x₂ = a.cos(pt + p) (cm) có phương trình dao động tổng hợp là

A. x = a$\sqrt{2}$cos(pt +2p/3)(cm)                                               B. x = a.cos(pt +p/2)(cm)

C. x = 3a/2.cos(pt +p/4)(cm)                                                         D. x = 2a/3.cos(pt +p/6)(cm)                            Chọn B

  Giải: Với máy FX570ES : Bấm chọn MODE 2 màn hình xuất hiện chữ: CMPLX   chọn đơn vị góc  tính theo độ (D)  Bấm : SHIFT MODE 3          ( Lưu ý : Không nhập a)

Tìm dao động tổng hợp: Nhập máy :$\sqrt{2}$SHIFT(-)Ð45 +  1 SHIFT(-)Ð180 =  Hiển thị: 1Ð 90,   

5. Tìm dao động thành phần ( xác định A₂ và  j₂ ) bằng cách dùng máy tính thực hiện phép trừ:

  Ví dụ tìm dao động thành phần x₂:   x₂ =x - x₁         với:  x₂ = A₂cos(wt + j₂)

  Xác định  A₂ và j₂?

 a.Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện chữ: CMPLX

   -Chọn đơn vị đo góc là  độ ta bấm:  SHIFT MODE 3   màn hình hiển thị chữ D

  (hoặc Chọn đơn vị đo góc là Radian ta bấm: SHIFT MODE 4  màn hình hiển thị chữ R )

  Nhập A , bấm SHIFT (-) nhập φ_; bấm - (trừ),  Nhập A₁ , bấm SHIFT (-) nhập φ_{1  ,} nhấn = kết quả.

   (Nếu hiển thị  số phức thì  bấm SHIFT 2  3  =  hiển thị kết quả trên màn hình là:  A₂ Ð j₂

 b.Với máy FX570MS : Bấm  MODE 2   màn hình xuất hiện chữ: CMPLX

  Nhập A , bấm SHIFT (-) nhập φ ;bấm  - (trừ), Nhập A₁ , bấm SHIFT (-) nhập φ₁   nhấn = 

  Sau đó bấm SHIFT  +  =  hiển thị kết quả là: A_2.  bấm  SHIFT   =   hiển thị kết quả là:  φ₂

  

Ví dụ 1:  Một chất điểm dao động điều hoà có phương trình dao động tổng hợp x=5$\sqrt{2}$cos(pt+5p/12)(cm)  với các dao động thành phần cùng phương, cùng tần số là x₁=A₁ cos(pt + j₁) và x₂=5cos(pt+p/6)(cm), Biên độ và pha ban đầu của dao động 1 là:

   A. 5cm; j₁ = 2p/3       B.10cm; j₁= p/2               C.5\sqrt{2}(cm) j₁ = p/4                  D. 5cm; j₁= p/3

  Giải: Với máy FX570ES : Bấm MODE 2  màn hình xuất hiện chữ: CMPLX

          -Chọn đơn vị đo góc là rad (R): SHIFT MODE  4 .  Tìm dao động thành phần:

         Nhập máy : 5$\sqrt{2}$SHIFT(-) Р (5p/12) – 5  SHIFT(-)  Ð (p/6  =  Hiển thị: 5Ð $\frac{2\pi }{3}$  , chọn A

Ví dụ 2:  Một vật đồng thời tham gia 3 dao động cùng phương, cùng tần số có phương trình dao động: x₁ =2\sqrt{3}cos(2πt + p/3) (cm), x₂ = 4cos(2πt +p/6) (cm) và x₂ = A₃ cos(pt + j₃) (cm). Phương trình dao động tổng hợp có dạng x = 6cos(2πt - p/6) (cm). Tính biên độ dao động và pha ban đầu của dao động thành phần thứ 3:

   A. 8cm và - p/2 .             B. 6cm và p/3.               C. 8cm và p/6 .               D. 8cm và p/2.        Chọn A

   Giải: Với máy FX570ES : Bấm  MODE 2   màn hình xuất hiện chữ: CMPLX

Chọn đơn vị đo góc là rad (R) SHIFT MODE  4 . Tìm dao động thành phần thứ 3: x₃ = x - x₁ –x₂

Nhập: 6 SHIFT(-) Ð (-p/6) - 2$\sqrt{3}$SHIFT(-) Ð (p/3) -  4  SHIFT(-) Ð (p/6 =  Hiển thị: 8 Ð-$\frac{\pi }{2}$

C. BÀI TẬP TỔNG HỢP:

Bài 1. Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có các phương trình là: 4cos(10t + $\frac{\pi }{4}$)(cm) và x₂ = 3cos(10t +$\frac{3\pi }{4}$) (cm). Xác định vận tốc cực đại và gia tốc cực đại của vật.

 Hướng dẫn giải:

   Cách 1:  Ta có: 

ð v_max = wA = 50 cm/s = 0,5 m/s; a_max = wA = 500 cm/s² = 5 m/s².

   Cách 2: Với máy FX570ES : Bấm  MODE 2  màn hình xuất hiện chữ: CMPLX

chọn đơn vị góc  tính theo độ (D)  Bấm : SHIFT MODE 3         

Tìm dao động tổng hợp: Nhập máy : 4SHIFT(-)Ð45 +  3 SHIFT(-)Ð135 =  Hiển thị: 5Ð 81,869,  

Suy ra A = 5cm  ⇒ v_max = wA = 50 cm/s = 0,5 m/s;  a_max = wA = 500 cm/s² = 5 m/s²..

Bài 2. Dao động tổng hợp của hai dao động điều hòa cùng phương có biểu thức  x = 5$\sqrt{3}$cos(6pt +$\frac{\pi }{2}$) (cm). Dao động thứ nhất có biểu thức là x₁ = 5cos(6pt +$\frac{\pi }{3}$ ) (cm). Tìm biểu thức của dao động  thứ hai.

       

         Vậy: x₂ = 5cos(6pt + $\frac{2\pi }{3}$)(cm).

        Cách 2:  Với máy FX570ES : Bấm MODE 2   màn hình xuất hiện chữ: CMPLX.Chọn đơn vị đo góc là rad (R) SHIFT MODE  4 . Tìm dao động thành phần thứ 2: x₂ = x - x₁

Nhập: 5$\sqrt{3}$SHIFT(-) Ð (p/2) -  5  SHIFT(-) Ð (p/3 =  Hiển thị: 5 Ð$\frac{2\pi }{3}$.Vậy: x₂ = 5cos(6pt + $\frac{2\pi }{3}$)(cm).

Bài 2.  Một vật tham gia đồng thời ba dao động điều hòa cùng phương với các phương trình: x₁ = 5cos5pt (cm);  x₂ = 3cos(5pt +$\frac{\pi }{2}$) (cm) và x₃ = 8cos(5pt - $\frac{\pi }{2}$) (cm). Xác định phương trình dao động tổng hợp của vật.

Cách 2:  Với máy FX570ES : Bấm MODE 2   màn hình xuất hiện chữ: CMPLX

Chọn đơn vị đo góc là rad (R) SHIFT MODE  4 . Tìm dao động thành phần thứ 2: x₂ = x - x₁

Nhập: 5$\sqrt{3}$SHIFT(-) Ð (p/2) -  5  SHIFT(-) Ð (p/3)=  Hiển thị: 5 Ð$\frac{2\pi }{3}$.Vậy: x₂ = 5cos(6pt + $\frac{2\pi }{3}$)(cm).

Bài 3.  Một vật tham gia đồng thời ba dao động điều hòa cùng phương với các phương trình: x₁ = 5cos5pt (cm);  x₂ = 3cos(5pt +$\frac{\pi }{2}$) (cm) và x₃ = 8cos(5pt - $\frac{\pi }{2}$) (cm). Xác định phương trình dao động tổng hợp của vật

Hướng dẫn giải:.

     Cách 1:  Ta có: x₁ = 3sin(5pt + $\frac{\pi }{2}$) (cm) = 3cos5pt (cm);   x₂ và x₃ ngược pha nên : 8-3 =5 =>

  x₂₃ =5cos(5pt - $\frac{\pi }{2}$) (cm),  x₁ và x₂₃  vuông pha . Vậy: x = x₁ + x₂ + x₃ = 5$\sqrt{2}$cos(5pt - $\frac{\pi }{4}$) (cm).

    Cách 2: Với máy FX570ES : Bấm MODE 2  màn hình xuất hiện chữ: CMPLX

    Chọn đơn vị góc tính rad (R). SHIFT MODE  4 Tìm dao động tổng hợp, nhập máy:

   5 SHIFT(-)Ð 0 + 3 SHIFT(-)Ð (p/2) + 8 SHIFT(-)Ð (-p/2)  =   Hiển thị: 5$\sqrt{2}$Ð -p/4.  Chọn A

BÀI TẬP TỰ LUYỆN

Bài 1: Một vật thực hiện đồng thời hai dao động cùng phương cùng tần số và cùng biên độ có pha ban đầu là $\frac{\pi }{3}$và $-\frac{\pi }{6}$ Pha của dao động tổng hợp là

A. $-\frac{\pi }{2}$                          B.$\frac{\pi }{4}$                   C.$\frac{\pi }{6}$                   D.$\frac{\pi }{12}$

Bài 3: Một vật thực hiện đồng thời hai dao động cùng phương cùng tần số f=10Hz. Có biên độ A1=7cm; A2=8cm độ lệch pha của hai dao động là $\frac{\pi }{3}$.  Vận tốc của vật ứng với li độ tổng hợp x=12cm bằng

A. \[\pm 10\pi \]m/s                 B. \[\pm 10\pi \]cm/s                         C. \[\pm \pi \]m/s                           D. \[\pm \pi \]cm/s

Bài 4*: Chuyển động của một vật là tổng hợp hai dao động điều hòa cùng phương cùng tần số có phương trình là: x1=4cos(10t+\[\pi \]/4) cm; x2=3cos(10t-3\[\pi \]/4) cm. Độ lớn vận tốc khi nó qua vị trí cân bằng là

A. 10cm/s                                B. 7cm/s                                             C. 20cm/s                                       D. 5cm/s

Bài 5: Một vật thực hiện đồng thời hai dao động cùng phương cùng tần số có phương trình x1=6cos(5\[\pi \]t+\[\pi \]/3) cm, x2= 8cos(5\[\pi \]t+4\[\pi \]/3) cm. Phương trình dao động tổng hợp là

A. x=14cos(5\[\pi \]t+\[\pi \]/3) cm                                          B. x=2cos(5\[\pi \]t+\[\pi \]/3) cm.

C. x=10cos(5\[\pi \]t+\[\pi \]/3) cm                                          D. x=2cos(5\[\pi \]t+4\[\pi \]/3) cm

Bài 6: Chuyển động của một vật là tổng hợp hai dao động điều hòa cùng phương cùng tần số có phương trình là: x1=4cos(10t+\[\pi \]/4) cm; x2=3cos(10t-3\[\pi \]/4) cm. Gia tốc khi nó qua vị trí  biên bằng

A. 10cm/s²                   B. 1cm/s²                     C. 10m/s²                     D. 1m/s²

Bài 7: Một vật thực hiện đồng thời hai dao động cùng phương cùng tần số có phương trình x1=2cos(5\[\pi \]t+\[\pi \]/2) cm, x2=2cos(5\[\pi \]t) cm. Vận tốc của vật lớn nhất bằng

A. 10\[\sqrt{2}\]\[\pi \] cm/s                B. 10\[\sqrt{2}\]cm/s                           C.10\[\pi \]cm/s                   D. 10cm/s 

Bài 8*: Một vật dao động trên một đường thẳng có phương trình x =3cos\[\omega \]t +4sin \[\omega \] t . Biên độ và pha ban đầu dao động này là

A. A=5cm; \[\phi \]=0,93 rad                                                                      B. A=1cm; \[\phi \]=0,93 rad  

C. A=1cm; \[\phi \]=3\[\pi \]/4 rad                                                              D. A=5cm; \[\phi \]=3\[\pi \]/4 rad

Bài 9:Dao động của một chất điểm có khối lượng 100g là tổng hợp  của hai dao động điều hòa cùng phương có phương trình li độ lần lượt là x1=5cos(10\[\pi \]t) cm, x2=10cos(5\[\pi \]t) cm (t tính bằng s). Chọn mốc thế năng ở VTCB. Cơ năng của chất điểm bằng

A. 220J                                    B. 0,1125J                                C. 0,22J                                 D. 112,5J

Bài 10*: Cho 3 dao động cùng phương có phương trình lần lượt là  x1=2Acos(10\[\pi \]t+\[\pi \]/6), x2=2Acos(10\[\pi \]t+5\[\pi \]/6) và x3=A(10\[\pi \]t-\[\pi \]/2) (với x tính bằng m, t tính bằng s). Phương trình tổng hợp của ba dao động trên là.

A. x=Acos(10\[\pi \]t+\[\pi \]/2) cm                                              B. x=Acos(10\[\pi \]t-\[\pi \]/2) cm

C. x=Acos(10\[\pi \]t+5\[\pi \]/2) cm                                            D. x=Acos(10\[\pi \]t-5\[\pi \]/2) cm

Bài 11: Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là x₁ = 10cos(\[2\pi \]t + φ) cm và x₂ = A₂cos(\[2\pi \]t$-{\pi }/{2}\;$) cm thì dao động tổng hợp là x = Acos(\[2\pi \]t$-{\pi }/{3}\;$) cm. Khi năng lượng dao động của vật cực đại thì biên độ dao động A₂ có giá trị là:

A. $20/\sqrt{3}$cm                        B. $10\sqrt{3}$cm                       C. $10/\sqrt{3}$cm                     D. 20cm

Bài 12: Dao động của một chất điểm là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là x₁ = 3cos(\[\frac{2\pi }{3}\]t -\[\frac{\pi }{2}\] ) và x₂ =3\[\sqrt{3}\]cos\[\frac{2\pi }{3}\]t  (x₁ và x₂ tính bằng cm, t tính bằng s). Tại các thời điểm x₁ = x₂ li độ của dao động tổng hợp là:
A. ± 5,79 cm.                               B. ± 5,19cm.                                    C. ± 6 cm.                                   D. ± 3 cm.

Bài 13. Dao động tổng hợp của 2 trong 3 dao động điều hòa cùng phương cùng tần số:x₁₂=2cos(2πt + π/3) cm, x₂₃=2\[\sqrt{3}\]cos(2πt +5π/6)mcm, x₃₁=2cos(2πt + π)cm. Biên độ dao động của thành phần thứ 2?
A,1 cm.                                      B. 3 cm.                                           C. $\sqrt{3}$cm.                    D.$2\sqrt{3}$cm

ĐÁP ÁN

1D        2D        3C          4A            5D            6D             7A           8A           9B            10A           11B          12B          13C

 

Bài viết gợi ý: