TỔNG HỢP VÀ PHÂN TÍCH LỰC ĐIỀU KIỆN CÂN BẰNG CỦA CHẤT ĐIỂM

TỔNG HỢP VÀ PHÂN TÍCH LỰC

ĐIỀU KIỆN CÂN BẰNG CỦA CHẤT ĐIỂM

I, LÝ THUYẾT

a) Lực, cân bằng lực

- Lực là đại lượng vectơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng

- Các lực cân bằng là các lực khi tác dụng đồng thời một vật thì không gây ra gia tốc cho vật

- Đường thẳng mang vectơ lực gọi là giá của lực. Hai lực cân bằng là hau lực cùng tác dụng lên 1 vật, cùng giá, cùng độ lớn và ngược chiều.

- Đơn vị cảu lực là niutơn (N).

b) Tổng hợp lực

-Tổng hợp lực là thay thế các lực tác dụng đồng thời cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy .

- Quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đông quy biểu diễn hợp lực của chúng

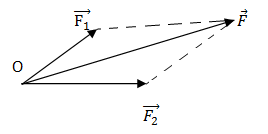
Ta có: \[\overset{\to }{\mathop {{F}_{1}}}\,\] +\[\overset{\to }{\mathop {{F}_{2}}}\,\]=\[\overset{\to }{\mathop F}\,\]

c) Điều kiện cân bằng của chất điểm

-Muốn cho một chất điểm đứng cân bằng thì hợp lực của các tác dụng lên nó phải cân bằng

Ta có: \[\overset{\to }{\mathop F}\,\] =\[\overset{\to }{\mathop {{F}_{1}}}\,\] +\[\overset{\to }{\mathop {{F}_{2}}}\,\]+…=\[\overset{\to }{\mathop 0}\,\]

d) Phân tích lực

- Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.

- Chỉ khi biết một lực có tác dụng cụ thể theo hai phương nào đó thì mới phân tích lực theo hai phương ấy

II, BÀI TẬP

a) Dạng 1: Tìm hợp lực của hai lực

Phương pháp tiến hành:

Bước 1. Tịnh tiến các lực về cùng điểm đặt.

Bước 2. Nếu các lực không cùng phương thì sử dụng quy tắc hình bình hành để xác định véc tơ tổng trên hình vẽ.

Bước 3. Sử dụng các công thức sau để tìm độ lớn của hợp lực.

\[{{F}^{2}}=F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \alpha \] với \[\alpha =\left( \overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}} \right)\].

\[\frac{F}{\sin {{\alpha }_{1}}}=\frac{{{F}_{1}}}{\sin {{\alpha }_{2}}}=\frac{{{F}_{2}}}{\sin {{\alpha }_{3}}}\] với\[{{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}\]là các góc đối diện với các lực tương ứng (định lí hàm số sin).

@ Các trường hợp đặc biệt

- Nếu \[{{F}_{1}}={{F}_{2}}=A\] thì \[F=A\sqrt{2+2\cos \alpha }=2A.\cos \frac{\alpha }{2}\].

- Nếu \[\overrightarrow{{{F}_{1}}}\bot \overrightarrow{{{F}_{2}}}\] thì \[F=\sqrt{F_{1}^{2}+F_{2}^{2}}\].

- Nếu \[\overrightarrow{{{F}_{1}}}\uparrow \uparrow \overrightarrow{{{F}_{2}}}\] thì \[F={{F}_{1}}+{{F}_{2}}\].

- Nếu \[\overrightarrow{{{F}_{1}}}\uparrow \downarrow \overrightarrow{{{F}_{2}}}\] thì \[F=\left| {{F}_{1}}-{{F}_{2}} \right|\].

F Lưu ý: Nếu có hai lực, thì hợp lực có giá trị trong khoảng: \[\left| {{F}_{1}}-{{F}_{2}} \right|\le {{F}_{hl}}\le \left| {{F}_{1}}+{{F}_{2}} \right|\].

Ví dụ 1: Cho hai lực đồng qui có độ lớn \[{{F}_{1}}={{F}_{2}}=20\left( N \right)\]. Độ lớn của hợp lực là \[F=34,6\left( N \right)\] khi hai lực thành phần hợp với nhau một góc là bao nhiêu?

Hướng dẫn:

Ta có: \[{{F}_{1}}={{F}_{2}}=20\left( N \right)\]nên \[F=20\sqrt{2+2\cos \alpha }=2.20.\cos \frac{\alpha }{2}\]

Vây góc$\alpha \approx {{60}^{0}}$

Ví dụ 2: Cho hai lực đồng qui có cùng độ lớn \[30\left( N \right)\]. Hỏi góc giữa hai lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng \[30\left( N \right)\]?

Hướng dẫn

Ta có: \[{{F}_{1}}={{F}_{2}}=30\] thì \[30=30\sqrt{2+2\cos \alpha }=2.30.\cos \frac{\alpha }{2}\].

Vậy góc $\alpha ={{120}^{0}}$

Ví dụ 3: Cho hai lực đồng quy có độ lớn \[4\left( N \right)\] và \[5\left( N \right)\] hợp với nhau một góc α. Tính góc α ? Biết rằng hợp lực của hai lực trên có độ lớn bằng \[7,8\left( N \right)\].

Hướng dẫn

Ta có: \[{{F}^{2}}=F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \alpha \]$\Leftrightarrow 7,{{8}^{2}}={{4}^{2}}+{{5}^{5}}+2.5.4.\cos \alpha $

Nên $\alpha ={{60}^{0}}15'$

Ví dụ 4: Một vật \[m=3\left( kg \right)\] được giữ yên trên mặt phẳng nghiêng góc \[{{45}^{o}}\] so với phương ngang bằng một sợi dây mảnh và nhẹ, bỏ qua ma sát. Tìm lực căng của sợi dây (lực mà tác dung lên sợi dây bị căng ra)?

Hướng dẫn:

Khi vật ở m ở vị trí cân bằng, ta có: \[\overset{\to }{\mathop P}\,\] +\[\overset{\to }{\mathop N}\,\] +\[\overset{\to }{\mathop T}\,\]

$\Leftrightarrow \overrightarrow{P}+\overrightarrow{P'}\Rightarrow \left| \overrightarrow{P} \right|=\left| \overrightarrow{P'} \right|$

Trong $\Delta P'NO$ ,ta có: $\frac{T}{P'}=\frac{T}{P}$ $\Rightarrow $ $T=P.\sin \alpha $

Mà $P=m.g$

$\Rightarrow T=m.g.\sin {{45}^{0}}=3.10.\frac{\sqrt{2}}{2}$ =$15\sqrt{2}$ (N)

Ví dụ 5: Một vật có khối lượng m chịu tác dụng của hai lực lực \[\overrightarrow{{{F}_{1}}}\] và \[\overrightarrow{{{F}_{2}}}\] như hình vẽ 4. Cho biết \[{{F}_{1}}=34,64\left( N \right);\text{ }{{F}_{2}}=20\left( N \right);\text{ }\alpha ={{30}^{o}}\] là góc hợp bởi \[\overrightarrow{{{F}_{1}}}\] với phương thẳng đứng. Tìm m để vật cân bằng ?

Hướng dẫn

Vật cân bằng thì: $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{P}=0$ (1)

Chọn hệ trục tọa độ Oxy góc hợp bởi trục Oy với $\overrightarrow{{{F}_{1}}}$ là $\alpha ={{30}^{o}}$ với $\overrightarrow{{{F}_{2}}}$ là $\beta $, $\overrightarrow{P}$ có phương thẳng đứng hướng xuống. $\overrightarrow{{{F}_{1}}}$ nằm bên phía âm tọa độ hướng lên $\overrightarrow{{{F}_{2}}}$ thì ngược lại. Gốc các vectơ tại điểm O. Từ điểm cuối $\overrightarrow{{{F}_{1}}}$ và $\overrightarrow{{{F}_{2}}}$ gióng vuông góc xuống Ox và Oy

Chiếu (1) lên Ox:

$-{{F}_{1}}\sin \alpha +{{F}_{2}}\sin \beta =0$ (2)

Chiếu (1) lên Oy

${{F}_{1}}\cos \alpha +{{F}_{2}}\cos \beta =P$ (3)

Từ (2) $\Rightarrow \sin \beta =\frac{{{F}_{1}}\sin \alpha }{{{F}_{2}}}=\frac{34,64.{}^{1}/{}_{2}}{20}=\frac{\sqrt{3}}{2}$

Nên: \[\cos \beta =\pm \frac{1}{2}\]

Thay \[\cos \beta =\pm \frac{1}{2}\] vào (3). Ta được $P=40N\Rightarrow m=4kg$ hoặc $P=20N\Rightarrow m=2kg$

BÀI TẬP TỰ LUYỆN

A, TRẮC NGHIỆM

1. Gọi F₁, F₂ là độ lớn của hai lực thành phần, F là hợp lực của chúng. Câu nào sau đây đúng

A. F không bao giờ nhỏ hơn cả F₁ và F₂ B. Trong mọi trường hợp, F thỏa mãn $\left| {{F}_{1}}-{{F}_{2}} \right|\le F\le {{F}_{1}}+{{F}_{2}}$

C. F không bao giờ bằng F₁ hoặc F₂ D. Trong mọi trường hợp F luôn luôn lớn hơn cả F₁ và F₂

2. Hãy chọn câu đúng: Nếu một vật đang chuyển động mà tất cả các lực tác dụng vào nó bỗng nhiên ngừng tác dụng thì:

A. Vật lập tức dừng lại

B. Vật chuyển động chậm dần rồi dừng lại

C. Vật chuyển động chậm dần trong một thời gian, sau đó sẽ chuyển động thẳng đều

D. Vật chuyển sang ngay trạng thái chuyển động thẳng đều

3. Chọn câu phát biểu đúng

A. Nếu thôi tác dụng lực vào vật thì vật đang chuyển động sẽ dừng lại

B. Nếu có lực tác dụng lên vật thì vận tốc của vật bị thay đổi

C. Nếu không có lực tác dụng vào vật thì vật không chuyển động được

D. Vật nhất thiết phải chuyển động theo hướng của lực tác dụng

4. Phát biểu nào sau đây là sai khi nói về khái niệm lực?

A. Lực là nguyên nhân gây ra chuyển động

B. Lực là nguyên nhân làm cho vật xuất hiện gia tốc hoặc bị biến dạng

C. Lực là đại lượng vectơ C. Lực là nguyên nhân làm cho vật thay đổi vận tốc

5. Điều nào sau đây là đúng khi nói về phép tổng hợp lực?

A. Phép tổng hợp lực thực chất là phép cộng tất cả các vectơ lực

B. Phép tổng hợp lực có thể thực hiện bằng quy tắc hình bình hành

C. Tổng hợp lực là phép thay thế nhiều lực tác dụng đồng thời vào một vật bằng một lực có tác dụng giống hệt như toàn bộ các lực ấy.

D. Các phát biểu a, b, c đều đúng

6. Hai người buộc hai sợi dây vào đầu một chiếc xe và kéo. Lực kéo chiếc xe lớn nhất khi:

A. Hai lực kéo vuông góc với nhau B. Hai lực kéo hợp với nhau góc 30⁰

C. Hai lực kéo cùng chiều với nhau D. Hai lực kéo ngược chiều với nhau

7. Trong trò chơi hai người kéo co, chọn câu đúng trong các câu nhận định sau:

A. Người thua kéo người thắng một lực bé hơn

B. Người thắng có thể kéo người thua một lực lớn hơn và cũng có thể bé hơn

C. Người thắng kéo người thua một lực bằng với người thua kéo người thắng.

D. Người thắng kéo người thua một lực lớn hơn

8. Lực của gió tác dụng vào cánh buồm của một chiếc thuyền là F₁ = 30N hướng về phía Bắc. Nước tác dụng vào thuyền một lực F₂ = 40N hướng về phía Đông. Thuyền có khối lượng 200kg. Hỏi độ lớn của gia tốc?

A..2,5 m/s² B.0,25 m/s² C.0,025 m/s² D.0,5 m/s²

9. Cặp “lực và phản lực” trong định luật III Newton

A.Tác dụng vào 2 vật khác nhau B.Tác dụng vào cùng một vật

C.Không cần phải bằng nhau về độ lớn D.Phải bằng nhau về độ lớn nhưng không cần cùng giá

10. Nếu lực tác dụng vào một vật đang chuyển động tăng lên gấp hai lần thì:

A.tốc độ của vật tăng lên gấp hai lần.

B.gia tốc của vật tăng gấp hai lần.

C. tốc độ của vật tăng lên hoặc giảm xuống gấp hai lần.

D. gia tốc của vật tăng lên hoặc giảm xuống gấp hai lần.

11. Phép phân tích lực cho phép ta:

A.thay thế một lực bằng một lực duy nhất.

B.thay thế một lực bằng một lực giống hệt nó.

C.thay thế một lực bằng một lực khác.

D.thay thế một lực bằng hai hay nhiều lực.

ĐÁP ÁN 1B 2D 3B 4A 5D 6C 7C 8B 9A 10B 11D

B) TỰ LUẬN

12. Một vật chịu tác dụng của ba lực như hình vẽ 5 thì cân bằng. Biết rằng độ lớn của lực \[{{F}_{3}}=40\left( N \right)\]. Hãy tính độ lớn của lực F₁ và F₂?

ĐS: \[{{F}_{1}}=23\left( N \right);\text{ }{{F}_{2}}=46\left( N \right)\]

13. Một chiếc đèn được treo vào tường nhờ một dây AB. Muốn cho đèn ở xa tường, người ta dùng một thanh chống nằm ngang, một đầu tì vào tường, còn đầu kia tì vào điểm B của dây như hình vẽ 6. Cho biết đèn nặng \[4\left( kg \right)\] và dây hợp với tường một góc \[{{30}^{o}}\]. Tính lực căng của dây và phản lực của thanh. Cho biết phản lực của thanh có phương dọc theo thanh và lấy \[g=10\left( m\text{/}{{s}^{2}} \right)\].

ĐS: \[15\left( N \right);\text{ }10\left( N \right)\].

14. Một vật có khối lượng \[m=5\left( kg \right)\] được treo vào cơ cấu như hình vẽ 7. Hãy xác định lực do vật nặng m làm căng các dây AC, AB ?

ĐS: \[57,7\left( N \right);\text{ }28,87\left( N \right)\].

15. Một vật có khối lượng \[m=3\left( kg \right)\] treo vào điểm chính giữa của dây thép AB có khối lượng không đáng kể như hình vẽ 8. Biết rằng \[AB=4\left( m \right);\text{ }CD=10\left( cm \right)\]. Tính lực kéo của mỗi sợi dây ?