Tư duy hình học THPT

Tư duy hình học THPT Quốc Gia

1. Tổng hợp những bài hay lạ trong đề thi các trường trong cả nước

2. Mang lại cái nhìn khái quát nhất về cách làm và tư duy nhìn hình.

Bài 01. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây cầu có 10nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m, biết 2 bên đầu cầu và giữa mối nhịp nối người ta xây 1 chân trụ rộng 5m. Bề dày và bề rộng của nhịp cầu không đổi là 20 cm (mặt cắt của một nhịp cầu được mô phỏng như hình vẽ). Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (làm tròn đến hàng đơn vị).

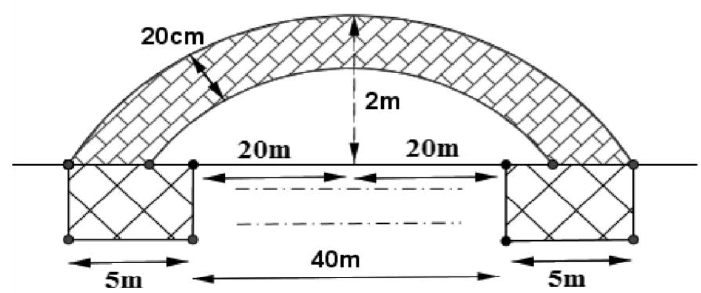
A.$20{{m}^{3}}$ B. $50{{m}^{3}}$ C. $40{{m}^{3}}$ D. $100{{m}^{3}}$

Bài 02. Từ một tấm tôn hình chữ nhật kích thước 40 cm x 60 cm người ta gò thành mặt xung quanh của một hình trụ có chiều cao 40 cm. Tính thể tích của khối trụ đó.

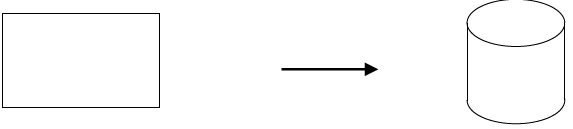
A.$\frac{144000}{\pi }c{{m}^{3}}$ B. $\frac{36000}{\pi }c{{m}^{3}}$ C. $\frac{48000}{\pi }c{{m}^{3}}$ D. $\frac{12000}{\pi }c{{m}^{3}}$

Bài 03. Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón, các kích thước cho trên hình vẽ (đơn vị đo là dm). Tính xem thể tích của khối dụng cụ đó là bao nhiêu dm³.

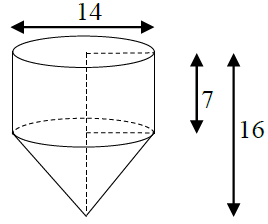
A.$490\pi $ B. $4900\pi $ C. $49000\pi $ D. $490000\pi $

Bài 04. Từ một tấm nhôm hình chữ nhật có kích thước 60 cm200 cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50 cm, theo hai cách sau (xem hình minh hoạ dướu đây):

Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

Cách 2: Gò tấm tôn thành bốn mặt xuang quanh của hình lăng trụ tứ giác đều.

Kí hiệu V₁ là thể tích của thùng gò được theo cách 1 và V₂ là thể tích thùng gò được theo cách 2. Tính tỉ số$k=\frac{{{V}_{1}}}{{{V}_{2}}}.$

A.$k=1$ B. $k=\frac{5}{\pi }$ C. $k=\frac{4}{\pi }$ D. $k=\frac{\pi }{4}$

Bài 05. Một tấm nhôm hình chữ nhật có chiều dài 12 cm và chiều rộng 8 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông cạnh bằng x cm, rồi gập tấm nhôm lại như hình vẽ để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

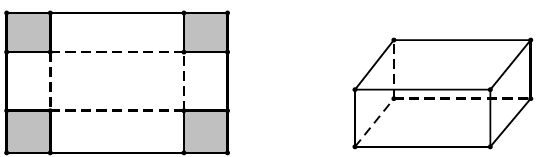
A.$x=\frac{10-2\sqrt{7}}{3}$ B.$x=\frac{12-3\sqrt{5}}{4}$ C. $x=\frac{12+3\sqrt{5}}{4}$ D. $x=\frac{10+2\sqrt{7}}{3}$

Bài 06. Một thùng rượu vỏ gỗ có bán kính đáy là 30 cm, bán kính lớn nhất ở thân thùng là 40 cm. Chiều cao của thùng rượu là 1 m. Hãy tính xem thùng rượu này chứa được bao nhiêu lít rượu (làm tròn đến chữ số thập phân thứ hai). Biết rằng cạnh bên hông của thùng rượu có hình dạng của parabol.

A.$\frac{15329\pi }{150}$ lít B. $\frac{502\pi }{3}$lít C. .$\frac{305\pi }{3}$ lít D.$\frac{406\pi }{3}$ lít

Bài 07.

Người ta khâu ghép các mảnh da hình lục giác đều màu trắng và ngũ giác đều màu đen để tạo thành quả bóng như hình vẽ. Hỏi có bao nhiêu mảnh da mỗi loại.

A. 12 mảnh da hình ngũ giác, 20 mảnh da hình lục giác.

B. 20 mảnh da hình ngũ giác, 20 mảnh da hình lục giác.

C. 10 mảnh da hình ngũ giác, 20 mảnh da hình lục giác.

D. 12 mảnh da hình ngũ giác, 24 mảnh da hình lục giác.

Bài 08. Một quả cầu lông và hộp đựng của nó có kích thước được cho trong hình vẽ. Hãy tính xem hộp đó đựng được bao nhiêu quả cầu lông.

A. 26 quả. B. 27 quả. C. 28 quả. D. 29 quả.

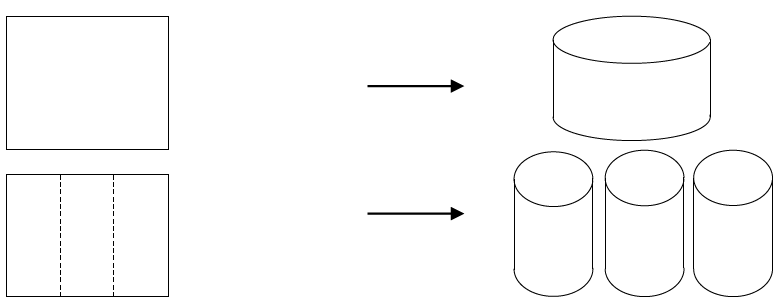
Bài 09. Từ một tấm nhôm hình vuông cạnh người ta làm các thùng đựng nước hình trụ có chiều 3mcao bằng 3 m, theo hai cách sau (xem hình minh hoạ dướu đây):

Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.

Cách 2: Cắt tấm tôn ban đầu thành ba tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quang của một thùng.

Kí hiệu${{V}_{1}}$ là thể tích của thùng gò được theo cách 1 và ${{V}_{2}}$ là tổng thể tích của hai thùng gò được

theo cách 2. Tính tỉ số$\frac{{{V}_{1}}}{{{V}_{2}}}$

A.\[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{1}{2}.\] B. \[\frac{{{V}_{1}}}{{{V}_{2}}}=1.\] C. \[\frac{{{V}_{1}}}{{{V}_{2}}}=2.\] D. \[\frac{{{V}_{1}}}{{{V}_{2}}}=3.\]

Bài 10. Người ta muốn làm một chiếc thùng hình trụ từ một miếng nhôm có chu vi 120 cm (quan sát hình minh hoạ). Hãy cho biết mảnh tôn có kích thước như thế nào thì thể tích của chiếc thùng lớn nhất. Biết rằng chiều cao của thùng bằng chiều rộng của miếng nhôm.

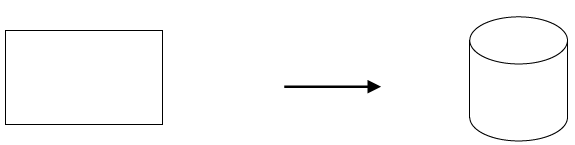
A. Dài 35 cm, rộng 25 cm. B. Dài 40 cm, rộng 20 cm.

C. Dài 50 cm, rộng 10 cm. D. Cả A, B, C đều sai.

Bài 11. Một hình chữ nhật có diện tích bằng 100 cm2. Hỏi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất.

A. 10 cm x 10 cm. B. 20 cm x 5 cm. C. 25 cm x 4 cm. D. Đáp án khác.

Bài 12. Một lão nông chia đất cho con trai để người con canh tác riêng, biết rằng người con sẽ được chọn miếng đất hình chữ nhật có chu vi 800 m. Hỏi anh ta phải chọn mảnh đất có kích thước như thế nào để diện tích đất canh tác là lớn nhất.

A. 300 m x 100 m B. 250 m x 150 m C. 350 m x 50 m D. Cả A, B, C đều sai.

Bài 13. Từ một tấm tôn hình chữ nhật kích thước 500 cm x 100 cm người ta gò thành mặt xung quanh của một hình trụ có chiều cao 50 cm. Tính thể tích của khối trụ đó.

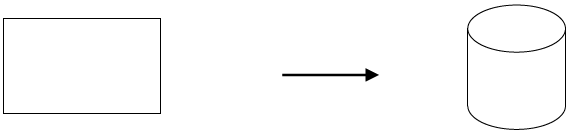
A.$\frac{15000}{3\pi }c{{m}^{3}}$ B. $\frac{125000}{\pi }c{{m}^{3}}$ C. $\frac{48000}{\pi }c{{m}^{3}}$ D. $\frac{12000}{\pi }c{{m}^{3}}$

Bài 14.

Một cốc nước hình trụ có chiều cao là 12 cm, đường kính đáy là 4 cm. Thả vào cốc 4 viên bi có đường kính 2 cm. Hỏi nước dâng cao cách mép cốc bao nhiêu cm, biết rằng lượng nước trong cốc cao 10 cm so với đáy cốc.

A.$\frac{1}{3}$ B.$\frac{2}{3}$ C. 0,75 D. 0,25

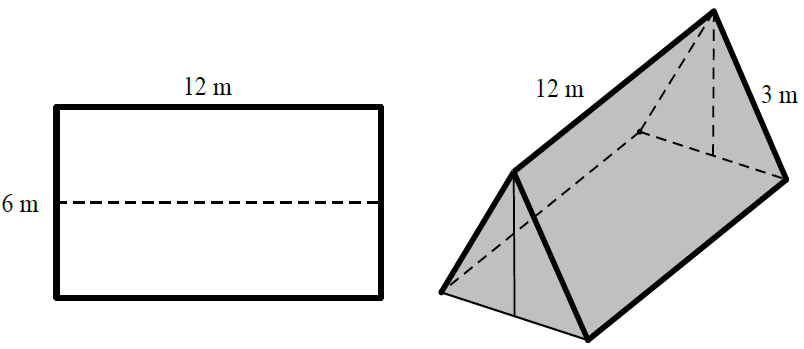
Bài 15. Một nhóm học sinh dựng lều khi đi dã ngoại bằng cách gấp đôi tấm bạt hình chữ nhật có chiều dài 12 m, chiều rộng 6 m (gấp theo đường trong hình minh hoạ) sau đó dùng hai cái gậy có chiều dài bằng nhau chống theo phương thẳng đứng vào hai mép gấp. Hãy tính xem khi dùng chiếc gậy có chiều dài bằng bao nhiêu thì không gian trong lều là lớn nhất.

A.$\sqrt{5}m.$ B. 1,5 m. C. 1 m. D. $\frac{3\sqrt{2}}{2}m.$

Bài 16. Một tấm nhôm hình tròn tâm O bán kính R được cắt thành hai miếng hình quạt, sau đó quấn thành hai hình nón (N₁) và (N₂). Gọi V₁ và V₂ lần lượt là thể tích của hai hình nón đó. Tính tỉ số $k=\frac{{{V}_{1}}}{{{V}_{2}}}$ biết$AOB={{90}^{\circ }}$

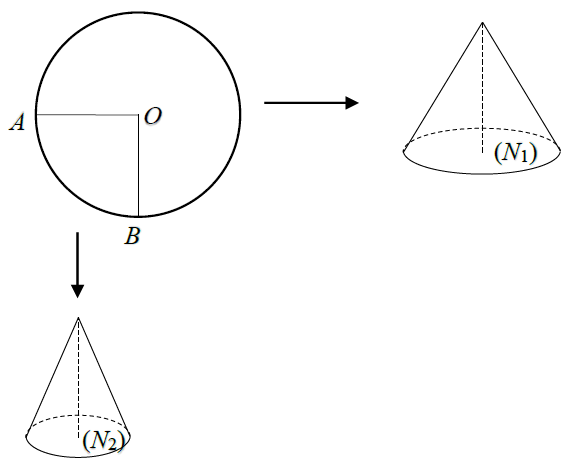
A. k = 2. B.$k=\frac{7\sqrt{105}}{9}.$ C. k = 3. D. $k=\frac{3\sqrt{105}}{5}.$

Hướng dẫn giải:

Bài 01.

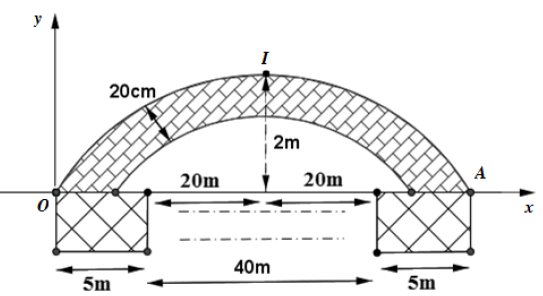
Chọn hệ trục toạ độ Oxy như hình vẽ. Gọi parabol đi qua điểm I là (P₁) và có phương trình: $y=a{{x}^{2}}+bx+x.$ Do ( P₁ )đi qua gốc toạ độ nên$({{P}_{1}}):y=a{{x}^{2}}+bx$

Sử dụng tiếp dữ kiện (P₁ ) đi qua I và A ta suy ra $({{P}_{1}}):y=-\frac{2}{625}{{x}^{2}}+\frac{4}{25}x$

Do đó parabol phía dưới có phương trình là$({{P}_{2}}):y=-\frac{2}{625}{{x}^{2}}+\frac{4}{25}x-\frac{1}{5}.$

Khi đó diện tích mỗi nhịp cầu là là $S=2{{S}_{1}}$ với ${{S}_{1}}$ phần diện tích giới hạn bởi các parabol$({{P}_{1}})$ và $({{P}_{2}})$ trong khoảng (0;25).

Suy ra:$S=2\left[ \int\limits_{0}^{0,2}{\left( -\frac{2}{625}{{x}^{2}}+\frac{4}{25}x \right)dx+\int\limits_{0,2}^{25}{\frac{1}{5}dx}} \right]=9,9({{m}^{2}}).$

Thể tích của mỗi nhịp cầu là:${{V}_{1}}=S.0,2=9,9.0,2=1,98({{m}^{3}}).$

Suy ra lượng bê tông để xây dựng các nhịp cầu là:$2.(1,98.10)=39,6({{m}^{3}})$ (*).

Do làm tròn đến hàng đơn vị nên ta cần$40{{m}^{3}}$

Chú ý: Tại (*) chúng ta nhân 2 vì là chúng ta phải xây dựng cả hai bên cầu.

Bài 02.$V=\pi {{7}^{2}}.7+\frac{1}{3}\pi {{7}^{2}}.9=490\pi .$

Bài 03. Ta có:$V={{(18-2x)}^{2}}.x=\frac{1}{4}(18-2x)(18-2x).4x\le \frac{1}{4}\frac{18-2x+18-2x+4x}{27}=\frac{1}{2}$

Đẳng thức xảy xa khi:$4x=18-2x\Leftrightarrow x=3$

Bài 04. Ta có$k=\frac{{{S}_{1}}}{{{S}_{2}}}=\frac{\pi {{\left( \frac{200}{2\pi } \right)}^{2}}}{{{\left( \frac{200}{4} \right)}^{2}}}=\frac{4}{\pi }$

Bài 05. Thể tích hộp là :$V(x)=7(12-2x)(8-2x).x$ .Thể tích hộp lớn nhất khi $x=\frac{10-2\sqrt{7}}{3}$

Bài 06.

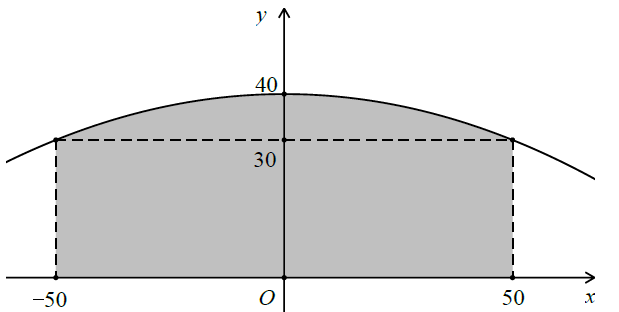
HD: Toạ độ hoá như hình vẽ. Thể tích của thùng rượu chính là thể tích của khối tròn xoay tạo thành khi quay hình thang cong giới hạn bởi đồ thị hàm số$y=-\frac{1}{250}{{x}^{2}}+40$ trục Ox và hai đường thẳng x = -50, x = 50 (như trong hình vẽ bên) xung quanh trục Ox. Công việc tính toán tiếp theo xin để lại cho bạn đọc.

Bài 07.

Gọi m là số mảnh da ngũ giác, n là số mảnh da lục giác (để cho thuận tiện tác giả gọi mảnh da ngũ giác là mảnh da đen, mảnh da lục giác là mảnh da trắng).

Số mảnh da của quả bóng là: . M = m + n.

Mỗi mảnh da đen tiếp xúc với 5 mảnh da trắng nên số đường khâu ghép giữa các mảnh da đen và các mảnh da trắng là 5m (1).

Mỗi mảnh da trắng tiếp xúc với 3 mảnh da đen nên số đường khâu ghép giữa các mảnh da trắng và các mảnh da đen là 3n (2).

Từ (1) và (2) ta có:$5m=3n\Leftrightarrow m=\frac{3n}{5}.$

Suy ra số mảnh da của quả bóng là:$m+n=\frac{3n}{5}+n=\frac{8n}{5}.$

Số đường khâu ghép giữa các mảnh da trắng với nhau là$\frac{3n}{2}$ . Vì cứ mỗi mảnh da trắng này lại tiếp xúc với 3 mảnh da trắng khác và mỗi đường khâu ghép ta đã đếm 2 lần.

Tổng số đường khâu ghép trên quả bóng là: Số đường khâu giữa các mảnh da cùng màu + Số đường khâu giữa các mảnh da khác màu$=3n+\frac{3n}{2}=\frac{9n}{2}.$

Số đỉnh của tất cả các mảnh da là 5m hay 3n (bằng tổng tất cả các đỉnh của các mảnh da đen).

Theo công thức Euler ta có: Số đỉnh + Số mặt = Số cạnh + 2 nên ta có:

$3n+\frac{8n}{5}=\frac{9n}{2}+2\Leftrightarrow \frac{1}{10}n=2\Rightarrow m=\frac{3.20}{5}=12.$

Bài 08. Ta có:$\frac{50-(9-1,5)}{1,5}28,(3).$ Suy ra số lượng quả cầu long đựng được trong hộp là 28 quả.

Bài 09. Gọi ${{R}_{1}}$ là bán kính đáy của khối trụ thứ nhất, ta có: $2\pi {{R}_{1}}=3\Leftrightarrow {{R}_{1}}=\frac{3}{2\pi }=>{{V}_{1}}=\frac{27}{4\pi }.$

Gọi R₂ là bán kính đáy của khối trụ thứ nhất, ta có:$2\pi {{R}_{2}}=1\Leftrightarrow {{R}_{2}}=\frac{1}{2\pi }=>{{V}_{2}}=\frac{9}{4\pi }.$

Suy ra: $\frac{{{V}_{1}}}{{{V}_{2}}}=3$

Bài 10. Gọi chiều dài là x thì chiều rộng là 60 – x .Bán kính đáy chiều cao h = 60 –x.

Suy ra:$V=\pi {{R}^{2}}h=\frac{-{{x}^{3}}+60{{x}^{2}}}{4\pi }.$

Xét hàm số:$f(x)=-{{x}^{3}}+60{{x}^{2}},x\in (0;60).$

Suy ra chiều dài bằng 40 cm, chiều rộng bằng 20 cm.

Bài 11. Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất. Bài toán này có thể giải quyết nhờ bất đẳng thức AM-GM hoặc khảo sát sự biến thiên của hàm số.

Bài 12. Gọi hai cạnh của miếng đất là x, y. Ta có: x + y = 400 (m).

Ta có:$xy\le \frac{{{(x+y)}^{2}}}{4}=\frac{{{400}^{2}}}{4}={{40000}^{2}}$

Đẳng thức xảy ra khi: x = y = 200 (m).

Bài 13. Gọi bán kính của cái thùng là r ta có:$2\pi r=100\Leftrightarrow r=\frac{50}{\pi }.$

Thể tích của cái hộp là:\[V=\pi {{r}^{2}}h=\pi {{\left( \frac{50}{\pi } \right)}^{2}}.50=\frac{125000}{\pi }(c{{m}^{3}})\]

Bài 14.

Thể tích của bốn viên bi là:$4.\left( \frac{4}{3}.\pi {{.1}^{3}} \right)=\frac{16\pi }{9}.$

Chiều cao nước dâng lên là: $\frac{16\pi }{9}:(\pi {{.2}^{2}})=\frac{4}{3}(cm).$ Như vậy nước sẽ cách mép cốc$\frac{2}{3}(cm).$

Bài 15 .

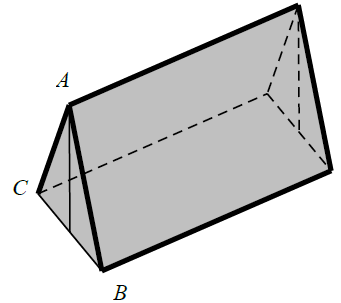
Không gian trong lều lớn nhất khi diện tích tam giác ABC lớn nhất.

Ta có:${{S}_{ABC}}=\frac{1}{2}AB.AC.\sin A=\frac{{{3}^{2}}}{2}\sin A\le \frac{9}{2}\sin {{90}^{\circ }}=\frac{9}{2}.$

Đẳng thức xảy ra khi:$ABC={{90}^{\circ }}$

Suy ra chiều cao của gậy chống là:$\frac{3.3}{\sqrt{{{3}^{2}}+{{3}^{2}}}}=\frac{3\sqrt{2}}{2}$

Bài 16. Gọi ${{r}_{1}},{{r}_{2}}$ lần lượt là bán kính đáy của hình nón $({{N}_{1}}),({{N}_{2}})$

Ta có:${{S}_{xq{{N}_{1}}}}=\pi {{r}_{1}}l=\frac{3}{4}\pi {{R}^{2}}=>{{r}_{1}}=\frac{3}{4}R;{{S}_{xq{{N}_{2}}}}=\pi {{r}_{2}}l=\frac{1}{4}\pi {{R}^{2}}=>{{r}_{2}}=\frac{1}{4}R.$

Suy ra:$\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\frac{1}{3}{{S}_{1}}{{h}_{1}}}{\frac{1}{3}{{S}_{2}}{{h}_{2}}}=\frac{\pi {{r}_{1}}^{2}\sqrt{{{R}^{2}}-{{r}_{1}}^{2}}}{\pi {{r}_{2}}^{2}\sqrt{{{R}^{2}}-{{r}_{2}}^{2}}}=\frac{\frac{9}{16}{{R}^{2}}.\frac{R\sqrt{7}}{4}}{\frac{1}{16}{{R}^{2}}.\frac{R\sqrt{15}}{4}}=\frac{3\sqrt{105}}{5}$