Viết biểu thức của điện áp u hoặc cường độ i
A)Tóm tắt lý thuyết:
1.Đoạn mạch chỉ chứa một phần tử (hoặc R, hoặc L, hoặc C):
-Đoạn mạch chỉ có điện trở thuần : u và i cùng pha nên \[{{\varphi }_{u}}\]=\[{{\varphi }_{i}}\]
Ta có: i=I\[\sqrt{2}\]cos(\[\omega t\]+\[{{\varphi }_{i}}\]) và u=\[{{U}_{R}}\]\[\sqrt{2}\]cos(\[\omega t\]+\[{{\varphi }_{i}}\]) với I=\[\frac{{{U}_{R}}}{R}\]
-Đoạn mạch chỉ có tụ điện: uc trễ pha so với i góc 
hay \[{{\varphi }_{u}}\]-\[{{\varphi }_{i}}\]= - 
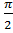
+Nếu đề cho i=I\[\sqrt{2}\]cos(\[\omega t\]) thì u =U\[\sqrt{2}\]cos(\[\omega t\]- 
) với I=\[\frac{{{U}_{C}}}{{{Z}_{C}}}\]; \[{{Z}_{_{C}}}\]=1\[\omega C\]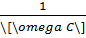
-Đoạn mạch chỉ có cuộn cảm thuần: \[{{u}_{L}}\]sớm pha hơn i góc π/2 hay \[{{\varphi }_{u}}\]-\[{{\varphi }_{i}}\]= 
+Nếu đề cho i=I\[\sqrt{2}\]cos(\[\omega t\]) thì u=U\[\sqrt{2}\]cos(\[\omega t\]+
) với I=\[\frac{{{U}_{L}}}{{{Z}_{L}}}\]; \[{{Z}_{L}}\]=\[\omega L\]
2.Đoạn mạch có R,L,C không phân nhánh:
-Phương pháp giải: Tìm Z, I (hoặc \[{{I}_{o}}\]) và \[\varphi \]
Bước 1:Tính tổng trở Z: Tính \[{{Z}_{L}}\]=\[\omega L\]; \[{{Z}_{_{C}}}\]=\[\frac{1}{\omega C}\]và Z=\[\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\]
Bước 2:Áp dụng định luật Ôm: U và I liên hệ với nhau bởi I=\[\frac{U}{Z}\]; \[{{I}_{0}}\]=\[\frac{{{U}_{o}}}{Z}\]
Bước 3:Tính độ lệch pha giữa u hai đầu mạch và i: tan\[\varphi \]=\[\frac{{{Z}_{L}}-{{Z}_{C}}}{R}\]
Bước 4:Viết biểu thức u hoặc i:
+Nếu cho trước : i=I\[\sqrt{2}\]cos(\[\omega t\]) thì biểu thức của u là u=U\[\sqrt{2}\]cos(\[\omega t\]+\[\varphi \])
Nhận xét:
-Nếu cho dòng điện một chiều qua cuộn dây thuần cảm thì cường độ dòng điện qua cuộn dây bằng 0
-Nếu cuộn dây có thêm r thì cuộn dây không thuần cảm \[{{\varphi }_{{{u}_{d}}}}\]-\[{{\varphi }_{i}}\]\[\ne \]
\[u={{u}_{R}}+{{u}_{L}}+{{u}_{C}}\]
\[\frac{{{u}_{L}}}{{{u}_{C}}}=-\frac{{{Z}_{L}}}{{{Z}_{C}}}=-\frac{{{U}_{L}}}{{{U}_{C}}}=-\frac{{{U}_{{{O}_{L}}}}}{{{U}_{{{O}_{C}}}}}\]
-Nếu mạch có R,L hoặc mạch có R,C luôn có:
\[{{(\frac{{{u}_{R}}}{{{U}_{{{O}_{R}}}}})}^{2}}+{{(\frac{{{u}_{L}}}{{{U}_{{{O}_{L}}}}})}^{2}}=1\]
\[{{(\frac{{{u}_{R}}}{{{U}_{{{O}_{R}}}}})}^{2}}+{{(\frac{{{U}_{C}}}{{{U}_{{{O}_{C}}}}})}^{2}}=1\]
-Đối với đoạn mạch RLC khi R và biểu thức u không đổi thì biểu thức của cường độ trước và sau khi nối tắt C :
\[{{i}_{1}}={{I}_{O}}\cos (\omega t+{{\varphi }_{1}})(A)\]
\[{{i}_{2}}={{I}_{O}}\cos (\omega t+{{\varphi }_{2}})(A)\]
Luôn có : \[{{\varphi }_{u}}=\frac{{{\varphi }_{{{i}_{1}}}}+{{\varphi }_{{{i}_{2}}}}}{2}\]
Lưu ý: Với đoạn mạch không phân nhánh có cuộn dây không thuần cảm (R,L,C,r) thì: Z=\[\sqrt{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\]và tan\[\varphi \]=\[\frac{{{Z}_{L}}-{{Z}_{C}}}{R+r}\]
B)Ví dụ minh họa:
Ví dụ 1: Điện áp hai đầu một đoạn mạch điện xoay chiều chỉ có điện trở thuần R=100\[\Omega \] có biểu thức \[u=200\sqrt{2}\cos (\omega t+\frac{\pi }{4})\](V). Biểu thức của cường độ dòng điện trong mạch là:
A.i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\] (A) B.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\] (A)
C.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\] (A) Di=\[2\cos (100\pi t-\frac{\pi }{2})(A)\]
Giải: Do mạch điện chỉ có R nên \[{{\varphi }_{u}}={{\varphi }_{i}}=\frac{\pi }{4}\]và \[{{I}_{O}}=\frac{{{U}_{O}}}{R}=2\sqrt{2}\]\[\Rightarrow \]Chọn đáp án B
Ví dụ 2: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có tụ có điện dung C=\[\frac{{{10}^{-4}}}{\pi }\](F) có biểu thức u=\[200\sqrt{2}\cos (100\pi t)(V)\]. Biểu thức của cường độ dòng điện trong mạch là:
A.i=\[2\sqrt{2}\cos (100\pi t+\frac{5\pi }{6})\] (A) B.i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\]
C.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\] (A) D.i=\[2\cos (100\pi t-\frac{\pi }{6})\]
Giải: \[{{Z}_{C}}=\frac{1}{\omega C}\] =100\[\Omega \] ; \[{{I}_{{{O}_{C}}}}=\frac{{{U}_{{{O}_{C}}}}}{{{Z}_{C}}}\]=2\[\sqrt{2}\]A
Do đoạn mạch chỉ có tụ điện nên \[{{\varphi }_{i}}={{\varphi }_{u}}+\frac{\pi }{2}=\frac{\pi }{2}\]\[\Rightarrow \]chọn đáp án C
Ví dụ 3: Hiệu điện thế giữa hai đầu một đoạn mạch điện xoay chiều có cuộn cảm có độ tự cảm L=\[\frac{1}{\pi }\](H) có biểu thức u=\[200\sqrt{2}\cos (100\pi t+\frac{\pi }{3})(V)\]. Biểu thức cường độ dòng điện trong mạch là:
A.i=\[2\sqrt{2}\cos (100\pi t+\frac{5\pi }{6})\](A) B.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\]
C.i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A) D.i=\[2\cos (100\pi t-\frac{\pi }{6})\]
Giải: ta có \[{{Z}_{L}}=L\omega \]=100\[\Omega \] ; I=\[\frac{{{U}_{{{O}_{L}}}}}{{{Z}_{L}}}=2\sqrt{2}\]A
Do đoạn mạch chỉ có cuộn cảm nên \[{{\varphi }_{i}}={{\varphi }_{u}}-\frac{\pi }{2}=-\frac{\pi }{6}\]\[\Rightarrow \]chọn đáp án C
Ví dụ 4: Mạch điện xoay chiều gồm một điện trở thuần R=50\[\Omega \], một cuộn thuần cảm có hệ số tự cảm L=\[\frac{1}{\pi }\](H) và một tụ điện có điện dung C=\[\frac{{{2.10}^{-4}}}{\pi }\](F) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng i=5cos100πt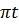
(A). Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
A.u=\[250\sqrt{2}\cos (100\pi t)\](V) B.u=\[250\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\]
C.u=250\[\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](V) D.u=250\[\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\]
Giải: có \[{{Z}_{L}}=L\omega =100\Omega \] ; \[{{Z}_{C}}=\frac{1}{C\omega }=50\Omega \] \[\to \]Z=\[\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=50\sqrt{2}\]
\[{{I}_{O}}=\frac{{{U}_{O}}}{Z}\to {{U}_{O}}=250\sqrt{2}\]V ; tan\[\varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}\]=\[\frac{\pi }{4}={{\varphi }_{u}}-{{\varphi }_{i}}\to {{\varphi }_{u}}=\frac{\pi }{4}\]\[\Rightarrow \]chọn đáp án D
Ví dụ 5: Đặt điện áp u=\[{{U}_{O}}\cos (100\pi t-\frac{\pi }{3})\](V) vào hai đầu một tụ điện có điện dung C=\[\frac{{{2.10}^{-4}}}{\pi }\](F). Ở thời điểm điện áp giữa hai đầu tụ điện là 150v thì cường độ dòng điện trong mạch là 4 A. Biểu thức của cường độ dòng điện trong mạch là:
A.i=\[4\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\](A) B.i=\[5\cos (100\pi t+\frac{\pi }{6})\]
C.i=\[5\cos (100\pi t-\frac{\pi }{6})\] (A) D.=\[4\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\]
Giải: có \[{{Z}_{C}}=\frac{1}{C\omega }=50\Omega \]
Với mạch thuần dung, điện áp và dòng điện vuông pha với nhau nên:
\[\frac{{{u}^{2}}}{{{U}_{O}}^{2}}+\frac{{{i}^{2}}}{{{I}_{O}}^{2}}=1\to {{I}_{O}}^{2}={{i}^{2}}+\frac{{{u}^{2}}}{{{Z}_{C}}^{2}}\] thay u và I vào ta được \[{{I}_{O}}\]=5A
Mạch điện thuần dung nên :\[\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=-\frac{\pi }{2}\to {{\varphi }_{i}}=-\frac{\pi }{3}+\frac{\pi }{2}=\frac{\pi }{6}\]
\[\Rightarrow \]Chọn đáp án B
C)Bài tập tự luyện:
Câu 1: Cho đoạn mạch gồm R, L, C mắc nối tiếp R=10\[\sqrt{3}\Omega \]; L=\[\frac{0,3}{\pi }\](H); C=\[\frac{{{10}^{-3}}}{2\pi }\](F). Đặt vào hai đầu đoặn mạch một hiệu điện thế u=\[100\sqrt{2}\cos (100\pi t)\](V). Viết biểu thức cường độ dòng điện trong mạch:
A.i=\[5\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A) B. i=\[5\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\]
C.i=\[5\cos (100\pi t-\frac{\pi }{6})\] (A) D.i=\[5\cos (100\pi t+\frac{\pi }{6})\]
Câu 2: Cho mạch điện xoay chiều có R, L, C mắc nối tiếp có R=30\[\Omega \], C=\[\frac{{{10}^{-4}}}{\pi }\](F), L thay đổi được cho hiệu điện thế hai đầu đoạn mạch là u=\[100\sqrt{2}\cos (100\pi t)\](V), để u nhanh pha hơn i góc \[\frac{\pi }{6}\] rad thì biểu thức i khi đó là:
A.i=\[\frac{5\sqrt{2}}{\sqrt{3}}\cos (100\pi t-\frac{\pi }{6})\](A) B. \[2\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\]
C. \[\frac{5\sqrt{2}}{\sqrt{3}}\cos (100\pi t+\frac{\pi }{6})\](A) D. \[2\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\]
Câu 3: Một mạch gồm cuộn dây thuần cảm có cảm kháng bằng 10Ω mắc nối tiếp với tụ điện có điện dung C=\[\frac{{{2.10}^{-4}}}{\pi }\]F. Dòng điện qua mạch có biểu thức i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{3})\]A. Biểu thức hiệu điện thế của hai đầu đoạn mạch là:
Au=\[80\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\] (A) B. u=\[80\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\]
C.u=\[120\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A) D.u=\[80\sqrt{2}\cos (100\pi t+\frac{2\pi }{3})\]
Câu 4: Một mạch điện gồm điện trở R=50Ω mắc nối tiếp với cuộn thuần cảm L=\[\frac{0,5}{\pi }\](H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u=\[100\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\](V). Biểu thức của cường độ dòng điện qua đoạn mạch là:
A. i=\[2\cos (100\pi t)\](A) B. i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\]
C. i=\[2\sqrt{2}\cos (100\pi t)\](A) D.i=\[2\cos (100\pi t-\frac{\pi }{2})\]
Câu 5 : Xét đoạn mạch gồm một điện trở hoạt động bằng 100Ω, một tụ điện có điện dung C=\[\frac{50}{\pi }\mu \](F), và một cuộn cảm thuần có độ tự cảm \[\frac{3}{\pi }\]H mắc nối tiếp . Nếu đặt vào hai đầu một điện áp u=\[200\cos (100\pi t)\](V) thì điện áp giữa hai đầu điện trở hoạt động có biếu thức:
A\[{{u}_{R}}=200\cos (100\pi t-\frac{\pi }{4})\](V) B. \[{{u}_{R}}=100\sqrt{2}\cos (100\pi t)\]
C. \[{{u}_{R}}=200\cos (100\pi t+\frac{\pi }{4})\](V) D. \[{{u}_{R}}=100\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\]
Câu 6: Đặt điện áp u=\[200\sqrt{2}\cos (100\pi t+\pi )\](V) vào hai đầu đoạn mạch có cuộn thuần cảm L=\[\frac{1}{\pi }\](H) thì cường độ dòng điện qua mạch là :
A.i =\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](A) B.i=\[4\cos (100\pi t-\frac{\pi }{2})\](A)
C.i =\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\](A) D.i=\[\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](A)
Câu 7: Đặt một hiệu điện thế xoay chiều vào hai đầu cuộn dây chỉ có độ thự cảm L=\[\frac{1}{2\pi }\]H thì cường độ dòng điện qua cuộn dây có biểu thức i=\[3\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\](A). Biểu thức nào sau đây là hiệu điện thế ở hai đầu đoạn mạch:
A.u=\[150\cos (100\pi t+\frac{2\pi }{3})\](V) B.u=\[150\sqrt{2}\cos (100\pi t-\frac{2\pi }{3})\]
C.u=\[150\sqrt{2}\cos (100\pi t+\frac{2\pi }{3})\](V) D.u=\[100\cos (100\pi t+\frac{2\pi }{3})\]
Câu 8: Khi đặt điện áp không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm \[\frac{1}{4\pi }\]H thì dòng điện trong mạch là dòng điện một chiều có cường độ 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp u=\[150\sqrt{2}\cos (120\pi t)\](V) thì biểu thức cường độ dòng điện trong đoạn mạch là:
A.i= \[5\sqrt{2}\cos (120\pi t-\frac{\pi }{4})\](A) B.i=\[5\cos (120\pi t+\frac{\pi }{4})\](A)
C.i=\[5\cos (120\pi t-\frac{\pi }{4})\](A) D.i=\[5\sqrt{2}\cos (120\pi t+\frac{\pi }{4})\](A)
Câu 9: Đặt điện áp xoay chiều u=\[{{U}_{O}}\cos (100\pi t+\frac{\pi }{3})\](V) vào hai đầu một cuộn cảm thuần có độ tự cảm L=\[\frac{1}{2\pi }\]H. Ở thời điểm điện áp giữa hai đầu cuộn cảm là 100\[\sqrt{2}\]V thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là:
A.i=\[2\sqrt{3}\cos (100\pi t+\frac{\pi }{6})\](A) B. i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A)
C.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\](A) C.i=\[2\sqrt{3}\cos (100\pi t-\frac{\pi }{6})\](A)
Câu 10: Đoạn mạch MN gồm các phần tử R=100Ω, L=\[\frac{2}{\pi }\]H và C=\[\frac{100}{\pi }\mu \]F ghép nối tiếp. Đặt điện áp u=\[220\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\](V) vào hai đầu đoạn mạch MN. Cường độ dòng điện tức thời qua mạch có biểu thức là:
A.i=\[2,2\sqrt{2}\cos (100\pi t-\frac{7\pi }{12})\]A B.i=\[2,2\cos (100\pi t-\frac{\pi }{2})\](A)
C.i=\[2,2\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\](A) D.i=\[2,2\cos (100\pi t-\frac{\pi }{6})\](A)
Câu 11: Đặt điện áp u=\[{{U}_{O}}\cos (100\pi t-\frac{\pi }{3})\](V) vào hai đầu một tụ điện có điện dung \[\frac{{{2.10}^{-4}}}{\pi }\]F. Ở thời điểm điện áp giữa hai đầu tụ điện là 150V thì cường độ dòng điện trong mạch là 4A. Biểu thức của cường độ dong điện trong mạch là:
A.i=\[5\cos (100\pi t-\frac{\pi }{6})\](A) B.i=\[5\cos (100\pi t+\frac{\pi }{6})\](A)
C.i=\[4\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\](A) D.i=\[4\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A)
Câu 12: Đặt điện áp xoay chiều u=\[200\sqrt{2}\cos (100\pi t)\](V) vào hai đầu đoạn mạch gồm tụ điện có dung kháng bằng 50Ω mắc nối tiếp với điện trở thuần R=50Ω. Cường độ dòng điện trong mạch có biểu thức:
A.i=\[4\cos (100\pi t-\frac{\pi }{2})\](A) B.i=\[4\cos (100\pi t+\frac{\pi }{4})\](A)
C.i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\](A) D.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\](A)
Câu 13:Một ấm đun nước có ghi 200V-800W, có độ tự cảm nhỏ không đáng kể, được mắc vào điện áp xoay chiều u=\[200\sqrt{2}\cos (100\pi t)\](V). Biểu thức cường độ dòng điện chạy qua ấm có dạng :
A.i=\[4\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](A) B.i=\[4\cos (100\pi t)\](A)
C.i=\[4\sin (100\pi t+\frac{\pi }{2})\](A) D.i=\[4\sqrt{2}sin(100\pi t+\frac{\pi }{2})\](A)
Câu 14: Dòng điện xoay chiều chạy qua một đoạn mạch chỉ có cuộn dây thuần cảm có độ tự cảm L=\[\frac{1}{\pi }\]H có biểu thức i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](A). Biểu thức điện áp xoay chiều giữa hai đầu đoạn mạch là:
A.u=\[200\cos (100\pi t-\frac{2\pi }{3})\](V) B.u=\[200\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](V)
C.u=\[200\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\](V) D.u=\[200\sqrt{2}\cos (100\pi t+\frac{\pi }{3})\](V)
Câu 15: Đặt điện áp xoay chiều có giá trị hiệu dụng 60V vào hai đầu đoạn mạch R, L, C mắc nối tiếp thì cường độ dòng điện qua đoạn mạch là \[{{i}_{1}}\]=\[{{I}_{O}}\cos (100\pi t+\frac{\pi }{4})\](A). Nếu ngắt bỏ tụ điện C thì cường độ dòng điện chạy qua đoạn mạch là \[{{i}_{2}}\]=\[{{I}_{O}}\]\[{{I}_{O}}\cos (100\pi t-\frac{\pi }{12})\](A). Điện áp hai đầu đoạn mạch là:
A.u=\[60\sqrt{2}\cos (100\pi t-\frac{\pi }{12})\](V) B.u=\[60\sqrt{2}\cos (100\pi t-\frac{\pi }{6})\](V)
C.u=\[60\sqrt{2}\cos (100\pi t+\frac{\pi }{12})\](V) D.u=\[60\sqrt{2}\cos (100\pi t+\frac{\pi }{6})\](V)
Câu 16: Cho ba linh kiện gồm điện trở thuần R=60Ω, cuộn cảm thuần L và tụ điện C. Lần lượt đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch nối tiếp RL hoặc RC thì biểu thức cường độ dòng điện trong mạch lần lượt là \[{{i}_{1}}=\]\[\sqrt{2}\cos (100\pi t-\frac{\pi }{12})\](A) và \[{{i}_{2}}\]=\[\sqrt{2}\cos (100\pi t+\frac{7\pi }{12})\](A). Nếu đặt điện áp vào hai đầu đoạn mạch RLC nối tiếp thì dòng điện trong mạch có biểu thức:
A.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{3})\](A) B.i=\[2\cos (100\pi t+\frac{\pi }{3})\](A)
C.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\](A) D.i=\[2\cos (100\pi t+\frac{\pi }{4})\](A)
Câu 17: Cho đoạn mạch điện AB không phân nhánh gồm cuộn cảm thuần , tụ điện có ddienj dung thay đổi được, một điện trở hoạt động 100Ω. Giữa A, B có một điện áp xoay chiều ổn định u= \[110\cos (100\pi t-\frac{\pi }{3})\](V). Cho C thay đổi. Khi C=\[\frac{125}{3\pi }\mu \]F thì điện áp hiệu dụng giữa hai đầu cuộn có giá trị lớn nhất. Biểu thức của điện áp giữa hai đầu cuộn cảm là :
A.\[{{u}_{L}}\]= \[220\sqrt{2}\cos (100\pi t+\frac{\pi }{2})(V)\] B. \[{{u}_{L}}\]= \[110\sqrt{2}\cos (100\pi t+\frac{\pi }{2})(V)\]
C. \[{{u}_{L}}\]= \[220\cos (100\pi t+\frac{\pi }{6})(V)\] D. \[{{u}_{L}}\]= \[110\sqrt{2}\cos (100\pi t+\frac{\pi }{6})(V)\]
Câu 18: Đặt điện áp u=\[120\cos (100\pi t+\frac{\pi }{3})\](V) vào hai đầu một đoạn mạch gồm cuộn cảm thuần mắc nối tiếp điện trở thuần R=30Ω thì điện áp hiệu dụng hai đầu cuộn cảm là 60V. Dòng điện tức thời qua đoạn mạch là:
A.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{12})\](A) B .i=\[2\sqrt{3}\cos (100\pi t+\frac{\pi }{6})\](A)
C.i=\[2\sqrt{2}\cos (100\pi t-\frac{\pi }{4})\](A) D.i=\[2\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\](A)
Câu 19:Cho đoạn mạch điện xoay chiều gồm cuộn dây thuần cảm và tụ điện mắc nối tiếp nhau. Điện áp hiệu dụng hai đầu cuộn cảm là 150V, giữa hai đầu tụ ddienj là 100V. Dòng điện trong mạch có biểu thức i=\[{{I}_{O}}\cos (100\pi t+\frac{\pi }{6})\](A). Biểu thức điện áp hai đầu đoạn mạch là:
A.u=\[50\sqrt{2}\cos (100\pi t-\frac{\pi }{2})\](V) B.u=\[50\sqrt{2}\cos (100\pi t+\frac{\pi }{2})\](V)
C.u=\[50\sqrt{2}\cos (100\pi t-\frac{2\pi }{3})\](V) D.u=\[50\sqrt{2}\cos (100\pi t+\frac{2\pi }{3})\](V)
Câu 20: Đặt vào hai đầu AMNB của đoạn mạch RLC nối tiếp gồm M là điểm nối giữa tụ điện và cuộn dây thuần cảm , N là điểm nối giữa cuộn dây và điện trở thuần. Khi đó biểu thức điện áp của hai đầu đoạn mạch NB là \[{{u}_{NB}}=\]\[60\sqrt{2}\cos (100\pi t-\frac{\pi }{3})\](V) và điện áp giữa hai đầu đoạn mạch AN sớm pha hơn điện áp hai đầu đoạn mạch AB góc \[\frac{\pi }{3}\]. Biểu thức của điện áp hai đầu đoạn mạch AB là:
A.u=\[60\sqrt{6}\cos (100\pi t-\frac{\pi }{6})\](V) B.u=\[40\sqrt{6}\cos (100\pi t-\frac{\pi }{6})\](V)
C.u=\[40\sqrt{6}\cos (100\pi t+\frac{\pi }{6})\](V) D.u=\[60\sqrt{6}\cos (100\pi t+\frac{\pi }{6})\](V)
Đáp án:
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
|
A |
A |
A |
D |
D |
A |
C |
C |
B |
B |
|
C11 |
C12 |
C13 |
C14 |
C15 |
C16 |
C17 |
C18 |
C19 |
C20 |
|
B |
B |
D |
D |
C |
D |
C |
A |
D |
A |
