kì thi giữa học kì môn toán

Gọi $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)={{2}^{x}}$ thỏa mãn $F\left( 0 \right)=\frac{1}{\ln 2}.$ Tính giá trị biểu thức $T=F\left( 0 \right)+F\left( 1 \right)+F\left( 2 \right)+...+F\left( 2017 \right).$ 

Biết Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ ${{R}_{1}}=20\,cm$, bán kính đường tròn lớn ${{R}_{2}}=30\,cm$ và mặt cắt khi cắt bới mặt phẳng đi qua trục, vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Tính thể tích không khí chứa được bên trong săm.

Biết $I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{x+x\cos x-{{\sin }^{3}}x}{1+\cos x}dx=\frac{{{\pi }^{2}}}{a}-\frac{b}{c}}$. Trong đó $a,\,b,\,c$ là các số nguyên dương, phân số $\frac{b}{c}$ tối giản. Tính  $T={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ 

Cho hàm số \[f\left( x \right)\]xác định trên \[\mathbb{R}\backslash \left\{ -1;1 \right\}\] và thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}-1}.$ Biết rằng $f\left( -3 \right)+f\left( 3 \right)=0$ và $f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=2.$Tính $T=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)$.

Biết $\int\limits_{-\frac{\pi }{6}}^{\frac{\pi }{6}}{\frac{x\cos x}{\sqrt{1+{{x}^{2}}}+x}\text{d}x}=a+\frac{{{\pi }^{2}}}{b}+\frac{\sqrt{3}\pi }{c}$với $a,\ b,\ c$ là các số nguyên. Tính $M=a-b+c$.

Cho miền phẳng $\left( D \right)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1,\,\,x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $\left( D \right)$quanh trục hoành.

Biết $\int\limits_{1}^{2}{\left( \sqrt[3]{x-\frac{1}{{{x}^{2}}}}+2\sqrt[3]{\frac{1}{{{x}^{8}}}-\frac{1}{{{x}^{11}}}} \right)dx}=\frac{a}{b}\sqrt[3]{c}$ , với $a,b,c$ nguyên dương , $\frac{a}{b}$ tối giản và $c

Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}\backslash \left\{ 0 \right\}$ thỏa mãn: ${{x}^{2}}{{f}^{2}}\left( x \right)+\left( 2x-1 \right)f\left( x \right)=x.{f}'\left( x \right)-1$ với $\forall x\in \mathbb{R}\backslash \left\{ 0 \right\}$đồng thời $f\left( 1 \right)=-2$. Tính $\int\limits_{1}^{2}{f\left( x \right)dx}$.  

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\left[ 0;1 \right]$ thỏa mãn $f\left( 1 \right)=0$,

$\int\limits_{0}^{1}{{{\left[ {f}'\left( x \right) \right]}^{2}}dx=\frac{3}{2}-2\ln 2}$ và $\int\limits_{0}^{1}{\frac{f\left( x \right)}{{{\left( x+1 \right)}^{2}}}dx}=2\ln 2-\frac{3}{2}$. Tính tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$ bằng

Cho hàm số $y=f\left( x \right)$ là hàm số chẵn và liên tục trên đoạn 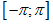thỏa mãn $\int\limits_{0}^{\pi }{f\left( x \right)dx=2018.}$ Tích phân $\int\limits_{-\pi }^{\pi }{\frac{f\left( x \right)}{{{2018}^{x}}+1}dx}$ bằng:

Cho hàm số $f\left( x \right)$ thỏa mãn ${{\left( {f}'\left( x \right) \right)}^{2}}+f\left( x \right).{f}''\left( x \right)=15{{x}^{4}}+12x$, $\forall x\in R$ và $f\left( 0 \right)={f}'\left( 0 \right)=1$. Giá trị của ${{f}^{2}}\left( 1 \right)$ bằng

Để đảm bảo an toàn giao thông , khi dừng đèn đỏ các xe cộ phải cách nhau tối thiếu 1m . Một ô tô A chạy với vận tốc 12m/s thì gặp ô tô B đang dừng đèn đỏ nên ô tô A phải hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức v$_{A}(t)=12-3t$ (m/s). Để đảm bảo an toàn thì ô tô A phải hãm phanh cách ô tô B một khoảng ít nhết bao nhiêu mét?

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên [0;p ]. Biết $f\left( 0 \right)=2e$ và $f\left( x \right)$ luôn thỏa mãn đẳng thức $f'\left( x \right)+\sin \,xf\left( x \right)=\cos x{{e}^{coxs}}\,\,\forall x\in \left[ 0;\pi  \right]$. Tính $I=\int\limits_{0}^{\pi }{f\left( x \right)dx}$ (làm tròn đến phần trăm) 

Cho hình phẳng (H) giới hạn bởi các đường $y=2x-{{x}^{2}}$, y=0. Khi quay (H) xung quanh trục Ox ta thu được khối tròn xoay có thể tích \[V=\pi \left( \frac{a}{b}+1 \right)\] , với$\frac{a}{b}$ là phân số tối giản . Khi đó có ab bằng bao nhiêu

Cho hàm số $f\left( x \right)=\frac{a}{{{\left( x+1 \right)}^{3}}}+bx{{e}^{x}}$. Tìm a và b biết rằng $f'\left( 0 \right)=-22$ và $\int\limits_{0}^{1}{f\left( x \right)dx=5}$ 

 Lúc 10 giờ sáng trên sa mạc, một nhà địa chất đang ở tại vị trí $A$, anh ta muốn đến vị trí $B$ (bằng ô tô) trước 12 giờ trưa, với $AB=70\,km.$ Nhưng trong  sa mạc thì xe chỉ có thể di chuyển với vận tốc là $30\,km/h$. Cách vị trí $A$ $10\,km$ có một con đường nhựa chạy song song với đường thẳng nối từ$A$ đến $B$. Trên đường nhựa thì xe có thể di chuyển với vận tốc $50\,km/h$. Tìm thời gian ít nhất để nhà địa chất đến vị trí $B$?

Cho hàm số $y=f(x)$ nghịch biến trên R và thỏa mãn $\left[ f(x)-x \right]f(x)={{x}^{6}}+3{{x}^{4}}+2{{x}^{2}},\forall x\in R$ . Giá trị $I=\int\limits_{1}^{2}{f(x)dx}$ bằng bao nhiêu?

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên đoạn \[[0;1]\] thỏa mãn $f\left( 1 \right)=1,\,\,\,\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}d\text{x=}\frac{9}{5}}$ và $\int\limits_{0}^{1}{f\left( \sqrt{x} \right)d\text{x}}=\frac{2}{5}.$ Tính tích phân $I=\int\limits_{0}^{1}{f\left( x \right)d\text{x}}$ 

Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=1;\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}dx}=9$ và $\int\limits_{0}^{1}{{{x}^{3}}f\left( x \right)dx=\frac{1}{2}.}$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$bằng :

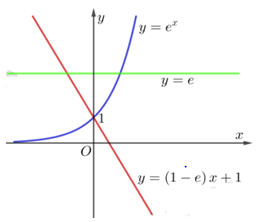
Cho $\left( H \right)$ là hình phẳng giới hạn bởi các đồ thị hàm số $y=e,y={{e}^{x}}$ và $y=\left( 1-e \right)x+1$ (tham khảo hình vẽ). Diện tích của $\left( H \right)$là

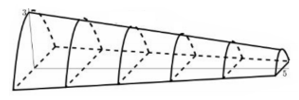
Cho một mô hình \[3-D\] mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài \[5\,\left( \text{cm} \right)\]; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức$y=3-\frac{2}{5}x$\[\left( \text{cm} \right)\], với $x$\[\left( \text{cm} \right)\] là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị$c{{m}^{3}}$ ) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị )

Cho hàm số $f\left( x \right)$ có đạo hàm không âm trên \[[0;1]\] thỏa mãn ${{\left[ f\left( x \right) \right]}^{4}}{{\left[ f'\left( x \right) \right]}^{2}}\left( {{x}^{2}}+1 \right)=1+{{\left[ f\left( x \right) \right]}^{3}}$ và $f\left( x \right)>0$ với \[\forall x\in [0;1],\] biết $f\left( 0 \right)=2.$  f(1) nằm trong khoảng nào trong các khoảng sau:

Cho hàm số \[f\left( x \right)\] có đạo hàm và liên tục trên đoạn \[\left[ 4;8 \right]\] và \[f\left( x \right)\ne 0\forall x\in \left[ 4;8 \right].\] Biết rằng \[\int\limits_{4}^{8}{\frac{{{\left[ f'\left( x \right) \right]}^{2}}}{{{\left[ f\left( x \right) \right]}^{4}}}dx}=1\] và \[f\left( 4 \right)=\frac{1}{4},f\left( 8 \right)=\frac{1}{2}.\] Tính \[f\left( 6 \right).\]

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -2;1 \right\}$ thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}+x-2},f\left( -3 \right)-f\left( 3 \right)=0$ và $f\left( 0 \right)=\frac{1}{3}.$ Giá trị biểu thức $f\left( -4 \right)+f\left( -1 \right)-f\left( 4 \right)$ bằng:

Cho hàm số\[f(x)\]có đạo hàm liên tục trên \[\mathbb{R}\] và thỏa mãn \[\int\limits_{0}^{1}{f(x)}\,\text{d}x=1\], \[f\left( 1 \right)=\cot 1\].

Tính tích phân \[I=\int\limits_{0}^{1}{\left( f\left( x \right){{\tan }^{2}}x+{f}'\left( x \right)\tan x \right)\,\text{d}x}\].

Biết $\int\limits_{1}^{2}{\frac{x}{3x+\sqrt{9{{x}^{2}}-1}}dx}=a+b\sqrt{2}+c\sqrt{35}$ với a, b, c là các số hữu tỉ, tính $P=a+2b+c-7.$ 

Cho hàm số $f\left( x \right)$ có đạo hàm dương, liên tục trên đoạn $\left[ 0;1 \right]$ thỏa mãn điều kiện $f\left( 0 \right)=1$ và $3\int\limits_{0}^{1}{\left[ f'\left( x \right).{{\left[ f\left( x \right) \right]}^{2}}+\frac{1}{9} \right]}\,dx\le 2\int\limits_{0}^{1}{\sqrt{f'\left( x \right)}.f\left( x \right)dx.}$ Tính $\int\limits_{0}^{1}{{{\left[ f\left( x \right) \right]}^{3}}dx.}$

Cho \[f(x)\] là hàm liên tục trên đoạn \[\text{ }\!\![\!\!\text{ }0;a]\] thỏa mãn

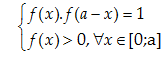 và \[\int\limits_{0}^{a}{\frac{dx}{1+f(x)}=\frac{ba}{c}},\] trong đó \[b,c\] là hai số nguyên dương và \[\frac{b}{c}\] là phân số tối giản. Khi đó \[b+c\] có giá trị thuộc khoảng nào dưới đây?

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $f\left( x \right)-8{{x}^{3}}f\left( {{x}^{4}} \right)+\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}+1}}=0$. Tích phân $I=\int\limits_{0}^{1}{f\left( x \right)dx}$ có kết quả dạng $\frac{a-b\sqrt{2}}{c}$ với $a,b,c\in \mathbb{R}$, $\frac{a}{c},\frac{b}{c}$ tối giản. Tính $a+b+c$.   

Cho số thực $a > 0.$ Giả sử hàm số $f\left( x \right)$ liên tục và luôn dương trên đoạn $\left[ {0;a} \right]$

thỏa mãn $f\left( x \right).f\left( {a - x} \right) = 1.$ Tính tích phân $I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}dx} $