nguyên hàm tích phân
Cho $f(x)$ là một hàm số liên tục trên R thỏa mãn $f(x)+f(-x)=\sqrt{2-2\cos 2x}$. Tính tích phân $I=\int\limits_{-\frac{3\pi }{2}}^{\frac{3\pi }{2}}{f(x)dx.}$
Gọi $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)={{2}^{x}}$ thỏa mãn $F\left( 0 \right)=\frac{1}{\ln 2}.$ Tính giá trị biểu thức $T=F\left( 0 \right)+F\left( 1 \right)+F\left( 2 \right)+...+F\left( 2017 \right).$
Cho số thực $a > 0.$ Giả sử hàm số $f\left( x \right)$ liên tục và luôn dương trên đoạn $\left[ {0;a} \right]$
thỏa mãn $f\left( x \right).f\left( {a - x} \right) = 1.$ Tính tích phân $I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}dx} $
Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=0$và ${{\int\limits_{0}^{1}{\left[ f'\left( x \right) \right]}}^{2}}dx=\int\limits_{0}^{1}{\left( x+1 \right){{e}^{x}}dx=\frac{{{e}^{2}}-1}{4}.}$ Tính tích phân $I=\int\limits_{0}^{1}{f\left( x \right)dx.}$
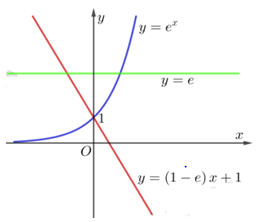
Cho $\left( H \right)$ là hình phẳng giới hạn bởi các đồ thị hàm số $y=e,y={{e}^{x}}$ và $y=\left( 1-e \right)x+1$ (tham khảo hình vẽ). Diện tích của $\left( H \right)$là
Cho hàm số $f\left( x \right)$ có đạo hàm dương, liên tục trên đoạn $\left[ 0;1 \right]$ thỏa mãn điều kiện $f\left( 0 \right)=1$ và $3\int\limits_{0}^{1}{\left[ f'\left( x \right).{{\left[ f\left( x \right) \right]}^{2}}+\frac{1}{9} \right]}\,dx\le 2\int\limits_{0}^{1}{\sqrt{f'\left( x \right)}.f\left( x \right)dx.}$ Tính $\int\limits_{0}^{1}{{{\left[ f\left( x \right) \right]}^{3}}dx.}$
Cho hàm số $f\left( x \right)=\frac{a}{{{\left( x+1 \right)}^{3}}}+bx{{e}^{x}}$. Tìm a và b biết rằng $f'\left( 0 \right)=-22$ và $\int\limits_{0}^{1}{f\left( x \right)dx=5}$
Cho hàm số $f(x)$ xác định trên $\mathbb R\backslash\{\frac12\}$ thỏa mãn $f'(x)=\dfrac2{2x-1}$, $f(0)=1$ và $f(1)=2$. Giá trị của biểu thức $f(-2)+f(2)$ bằng
Giá trị của tích phân \[\int_{0}^{100}{x\left( x-1 \right)...\left( x-100 \right)dx}\] bằng
Cho hàm số \[f\left( x \right)\] có đạo hàm và liên tục trên đoạn \[\left[ 4;8 \right]\] và \[f\left( x \right)\ne 0\forall x\in \left[ 4;8 \right].\] Biết rằng \[\int\limits_{4}^{8}{\frac{{{\left[ f'\left( x \right) \right]}^{2}}}{{{\left[ f\left( x \right) \right]}^{4}}}dx}=1\] và \[f\left( 4 \right)=\frac{1}{4},f\left( 8 \right)=\frac{1}{2}.\] Tính \[f\left( 6 \right).\]
Lúc 10 giờ sáng trên sa mạc, một nhà địa chất đang ở tại vị trí $A$, anh ta muốn đến vị trí $B$ (bằng ô tô) trước 12 giờ trưa, với $AB=70\,km.$ Nhưng trong sa mạc thì xe chỉ có thể di chuyển với vận tốc là $30\,km/h$. Cách vị trí $A$ $10\,km$ có một con đường nhựa chạy song song với đường thẳng nối từ$A$ đến $B$. Trên đường nhựa thì xe có thể di chuyển với vận tốc $50\,km/h$. Tìm thời gian ít nhất để nhà địa chất đến vị trí $B$?
Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -2;1 \right\}$ thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}+x-2},f\left( -3 \right)-f\left( 3 \right)=0$ và $f\left( 0 \right)=\frac{1}{3}.$ Giá trị biểu thức $f\left( -4 \right)+f\left( -1 \right)-f\left( 4 \right)$ bằng:
Cho hàm số \[f\left( x \right)\]xác định trên \[\mathbb{R}\backslash \left\{ -1;1 \right\}\] và thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}-1}.$ Biết rằng $f\left( -3 \right)+f\left( 3 \right)=0$ và $f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=2.$Tính $T=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)$.
Cho \[\int\limits_{0}^{2}{\left( 1-2x \right)f'\left( x \right)dx}=3f\left( 2 \right)+f\left( 0 \right)=2016.\] Tích phân \[\int\limits_{0}^{1}{f\left( 2x \right)dx}\] bằng:
Biết $\int\limits_{1}^{2}{\frac{x}{3x+\sqrt{9{{x}^{2}}-1}}dx}=a+b\sqrt{2}+c\sqrt{35}$ với a, b, c là các số hữu tỉ, tính $P=a+2b+c-7.$
Cho miền phẳng $\left( D \right)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1,\,\,x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $\left( D \right)$quanh trục hoành.
Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}\backslash \left\{ 0 \right\}$ thỏa mãn: ${{x}^{2}}{{f}^{2}}\left( x \right)+\left( 2x-1 \right)f\left( x \right)=x.{f}'\left( x \right)-1$ với $\forall x\in \mathbb{R}\backslash \left\{ 0 \right\}$đồng thời $f\left( 1 \right)=-2$. Tính $\int\limits_{1}^{2}{f\left( x \right)dx}$.
Cho \[f(x)\] là hàm liên tục trên đoạn \[\text{ }\!\![\!\!\text{ }0;a]\] thỏa mãn
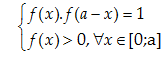 và \[\int\limits_{0}^{a}{\frac{dx}{1+f(x)}=\frac{ba}{c}},\]
trong đó \[b,c\] là hai số nguyên dương và \[\frac{b}{c}\] là phân số tối giản.
Khi đó \[b+c\] có giá trị thuộc khoảng nào dưới đây?
và \[\int\limits_{0}^{a}{\frac{dx}{1+f(x)}=\frac{ba}{c}},\]
trong đó \[b,c\] là hai số nguyên dương và \[\frac{b}{c}\] là phân số tối giản.
Khi đó \[b+c\] có giá trị thuộc khoảng nào dưới đây?
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên đoạn \[[0;1]\] thỏa mãn $f\left( 1 \right)=1,\,\,\,\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}d\text{x=}\frac{9}{5}}$ và $\int\limits_{0}^{1}{f\left( \sqrt{x} \right)d\text{x}}=\frac{2}{5}.$ Tính tích phân $I=\int\limits_{0}^{1}{f\left( x \right)d\text{x}}$
Biết $\int\limits_{-\frac{\pi }{6}}^{\frac{\pi }{6}}{\frac{x\cos x}{\sqrt{1+{{x}^{2}}}+x}\text{d}x}=a+\frac{{{\pi }^{2}}}{b}+\frac{\sqrt{3}\pi }{c}$với $a,\ b,\ c$ là các số nguyên. Tính $M=a-b+c$.
Cho hàm số $y=f\left( x \right)$ thỏa mãn $f'\left( x \right).f\left( x \right)={{x}^{4}}+{{x}^{2}}$. Biết $f\left( 0 \right)=2$. Tính ${{f}^{2}}\left( 2 \right).$
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\left[ 0;1 \right]$ thỏa mãn $f\left( 1 \right)=0$,
$\int\limits_{0}^{1}{{{\left[ {f}'\left( x \right) \right]}^{2}}dx=\frac{3}{2}-2\ln 2}$ và $\int\limits_{0}^{1}{\frac{f\left( x \right)}{{{\left( x+1 \right)}^{2}}}dx}=2\ln 2-\frac{3}{2}$. Tính tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$ bằng
Biết $I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{x+x\cos x-{{\sin }^{3}}x}{1+\cos x}dx=\frac{{{\pi }^{2}}}{a}-\frac{b}{c}}$. Trong đó $a,\,b,\,c$ là các số nguyên dương, phân số $\frac{b}{c}$ tối giản. Tính $T={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$
Cho biết $\int\limits_{0}^{\frac{\pi }{4}}{\frac{\text{cos}x}{\operatorname{s}\text{inx}+c\text{osx}}dx=a\pi +b\ln 2}$ với $a\,$và $b$ là các số hữu tỉ. Khi đó \[\frac{a}{b}\] bằng:
Cho hàm số $f\left( x \right)=\frac{a}{{{\left( x+1 \right)}^{3}}}+bx{{e}^{x}}$. Tìm a và b biết rằng $f'\left( 0 \right)=-22$ và $\int\limits_{0}^{1}{f\left( x \right)dx=5}$
Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $f\left( x \right)-8{{x}^{3}}f\left( {{x}^{4}} \right)+\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}+1}}=0$. Tích phân $I=\int\limits_{0}^{1}{f\left( x \right)dx}$ có kết quả dạng $\frac{a-b\sqrt{2}}{c}$ với $a,b,c\in \mathbb{R}$, $\frac{a}{c},\frac{b}{c}$ tối giản. Tính $a+b+c$.
Cho hàm số $f\left( x \right)$ có đạo hàm không âm trên \[[0;1]\] thỏa mãn ${{\left[ f\left( x \right) \right]}^{4}}{{\left[ f'\left( x \right) \right]}^{2}}\left( {{x}^{2}}+1 \right)=1+{{\left[ f\left( x \right) \right]}^{3}}$ và $f\left( x \right)>0$ với \[\forall x\in [0;1],\] biết $f\left( 0 \right)=2.$ f(1) nằm trong khoảng nào trong các khoảng sau:
Biết $\int\limits_{1}^{2}{\left( \sqrt[3]{x-\frac{1}{{{x}^{2}}}}+2\sqrt[3]{\frac{1}{{{x}^{8}}}-\frac{1}{{{x}^{11}}}} \right)dx}=\frac{a}{b}\sqrt[3]{c}$ , với $a,b,c$ nguyên dương , $\frac{a}{b}$ tối giản và $c
Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=1;\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}dx}=9$ và $\int\limits_{0}^{1}{{{x}^{3}}f\left( x \right)dx=\frac{1}{2}.}$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$bằng :
Cho hàm số $y=f\left( x \right)$ là hàm số chẵn và liên tục trên đoạn 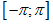 thỏa mãn $\int\limits_{0}^{\pi
}{f\left( x \right)dx=2018.}$ Tích phân $\int\limits_{-\pi }^{\pi
}{\frac{f\left( x \right)}{{{2018}^{x}}+1}dx}$ bằng:
thỏa mãn $\int\limits_{0}^{\pi
}{f\left( x \right)dx=2018.}$ Tích phân $\int\limits_{-\pi }^{\pi
}{\frac{f\left( x \right)}{{{2018}^{x}}+1}dx}$ bằng:
| 1 |
vodien0409
Nguyễn Trúc An
|
7/30
|
nguyên hàm tích phân
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm