đề 1 abcxyz

 Trong không gian với hệ  tọa độ $Oxyz,$ cho hai đường thẳng ${{d}_{1}}:\frac{x+1}{2}=\frac{y-1}{-1}=\frac{z-1}{1}$; ${{d}_{2}}:\frac{x-1}{1}=\frac{y-2}{1}=\frac{z+1}{2}$ và mặt phẳng $\left( P \right):x-y-2z+3=0.$ Biết đường thẳng $\Delta $nằm trên mặt phẳng $\left( P \right)$ và cắt cả hai đường thẳng ${{d}_{1}},{{d}_{2}}.$ Viết phương trình đường thẳng $\Delta $.

Trong không gian với hệ tọa độ Oxyz, cho điểm\[M(3;2;1)\]. Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

Trong không gian tọa độ Oxy, cho tam giác ABC biết $A\left( 1;0;-1 \right),\,\,B\left( 2;3;-1 \right),\,\,C\left( -2;1;1 \right)$. Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng $\left( ABC \right)$.

Trong không gian $Oxyz$, cho hai điểm $A\left( -2\,;\,3\,;\,2 \right)$ và $B\left( 2\,;\,1\,;\,0 \right)$. Mặt phẳng trung trực của $AB$ có phương trình là

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left( 3;-2;3 \right),B\left( 1;0;5 \right)$ và đường thẳng $\left( d \right):\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{2}.$ Tìm tọa độ điểm M trên đường thẳng $\left( d \right)$để $M{{A}^{2}}+M{{B}^{2}}$đạt giá trị nhỏ nhất.

Trong không gian Oxyz cho 2 đường thẳng \[{{d}_{1}}:\frac{x+3}{2}=\frac{y+2}{-1}=\frac{z+2}{-4};{{d}_{2}}:\frac{x+1}{3}=\frac{y+1}{2}=\frac{z-2}{3}\] và mặt phẳng \[\left( P \right):x+2y+3z-7=0.\] Đường thẳng vuông góc với mặt phẳng (P), cắt \[{{d}_{1}}\] và \[{{d}_{2}}\] có phương trình là:

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( -1;-2;0 \right),B\left( 0;-4;0 \right),$

$C\left( 0;0;-3 \right)$. Phương trình mặt phẳng $\left( P \right)$nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình

${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=1$, phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là:

Trong không gian với hệ tọa độ Oxyz cho điểm $M\left( 1;2;3 \right)$. Gọi $\left( P \right)$ là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng cách lớn nhất, mặt phẳng $\left( P \right)$ cắt các trục tọa độ tại các điểm A, B, C. Thể tích khối chóp O.ABC bằng:

Trong không gian với hệ tọa độ $Oxyz,$ tập hợp các điểm có tọa độ $\left( x;y;z \right)$ sao cho $-1\le x\le 3$,$-1\le y\le 3$,$-1\le z\le 3$ là tập các điểm của một khối đa diện (lồi) có một tâm đối xứng. Tìm tọa độ của tâm đối xứng đó.

Trong không gian với hệ trục Oxyz, cho 2 đường thẳng ${d_1},{d_2}$ lần lượt có phương trình ${d_1}:y = \frac{{x - 2}}{2} = \frac{{y - 2}}{1} = \frac{{z - 3}}{3};{d_2}:y = \frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 1}}{4}.$ Mặt phẳng cách đều 2 đường thẳng ${d_1},{d_2}$ có phương trình là 

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=16$ và các điểm \[A\text{ }\left( 1;0;2 \right),\text{ }B\text{ }\left( -1;2;2 \right).\] Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng \[ax+by+cx+3=0.\] Tính tổng \[T=a+b+c.\]

Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $A\left( 2\,;\ 1\ ;\ 1 \right)$ và mặt phẳng $(P):2x-y+2z+1=0$. Mặt cầu tâm $A$ tiếp xúc với mặt phẳng $(P)$ có phương trình

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng

Gọi S là tập hợp tất cả các số m sao cho đường thẳng ${{d}_{1}}$và ${{d}_{2}}$ chéo nhau và khoảng cách giữa chúng bằng $\frac{5}{\sqrt{19}}.$ Tính tổng các phần tử của S.

Trong không gian Oxyz, cho tam giác ABC với \[A\left( 1;-2;3 \right),B\left( -4;0;-1 \right)\] và \[C\left( 1;1;-3 \right).\] Phương trình mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[~A\left( -2;3;1 \right),\text{ }B\left( 2;1;0 \right)\] và \[C\text{ }\left( -3;-1;1 \right).\] Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy $AD$ và ${{S}_{ABCD}}=3{{S}_{\Delta ABC}}.$

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[A\left( 1;1;2 \right),B\left( -1;3;-9 \right)\]. Tìm tọa độ điểm M thuộc Oy sao cho $\Delta ABM$ vuông tại M .

Trong không gian Oxyz, cho \[A\left( 0;0;-3 \right),\text{ }B\left( 2;0;-1 \right)\]và mp $\left( P \right):3x-8y+7z-1=0.$ Có bao nhiêu điểm C trên mặt phẳng (P) sao cho ABC đều.

Trong không gian với hệ trục tọa độ \[Oxyz\], cho bốn điểm \[A\left( 2;-3;7 \right),B\left( 0;4;l \right),\] \[C\left( 3;0;5 \right),D\left( 3;3;3 \right).\] Gọi M là điểm nằm trên mặt phẳng \[\left( Oyz \right)\] sao cho biểu thức \[\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD} \right|\] đạt giá trị nhỏ nhất. Khi đó tọa độ M là:

Trong không gian Oxyz cho điểm $M\left( 1;3;-2 \right).$ Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục \[x'Ox;\text{ }y'Oy;\text{ }z'Oz~\] lần lượt tại ba điểm phân biệt A, B, C sao cho $OA=OB=OC\ne 0$.

Trong không gian với hệ trục tọa độ $Oxyz$, cho điểm $A\left( 1;2;3 \right)$. Gọi ${{A}_{1}},\,{{A}_{2}},\,{{A}_{3}}$ lần lượt là hình chiếu vuông góc của $A$ lên các mặt phẳng $\left( Oyz \right),\,\left( Ozx \right),\,\left( Oxy \right)$. Phương trình của mặt phẳng  $\left( {{A}_{1}}{{A}_{2}}{{A}_{3}} \right)$ là

Trong không gian với hệ tọa độ Oxyz, cho điểm$M\left( 2;1;0 \right)$và đường thẳng  $\Delta :\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-1}$. Phương trình tham số của đường thẳng d đi qua điểm M, cắt và vuông góc với $\Delta $ là

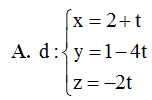
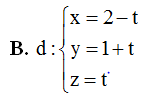
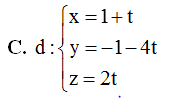
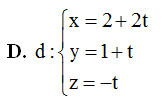
Trong không gian với hệ tọa độ $Oxyz,$cho mặt phẳng $\left( P \right)$ có phương trình $x+y-2z-6=0$ và mặt phẳng $\left( P' \right)$ có phương trình $-x-y+2z+2=0$. Xác định tập hợp tâm các mặt cầu tiếp xúc với $\left( P \right)$và  tiếp xúc với $\left( P' \right)$.

 Trong không gian với hệ tọa độ $Oxyz,$ cho mặt cầu $(S):{{(x-1)}^{2}}+{{(y-2)}^{2}}+{{(z-3)}^{2}}=9$ và đường thẳng $\Delta :\frac{x-6}{-3}=\frac{y-2}{2}=\frac{z-2}{2}.$ Phương trình mặt phẳng $\left( P \right)$ đi qua $M\left( 4;3;4 \right)$, song song với đường thẳng $\Delta $ và tiếp xúc với mặt cầu $\left( S \right)$ là

Trong hệ tọa độ Oxyz cho\[A(3,3,0),B(3,0,3),C(0,3,3)\]. Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:

Trong không gian  Oxyz,  cho ba điểm $A\left( a;0;0 \right),B\left( 0;b;0 \right),C\left( 0;0;c \right)$ với  a, b, c  là những số thực dương thay đổi sao cho ${{a}^{2}}+4{{b}^{2}}+16{{c}^{2}}=49.$ Tính tổng $F={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$sao cho khoảng cách từ  O đến (ABC) là lớn nhất.

Trong không gian $Oxyz,$ cho mặt phẳng \[\left( P \right):x-2y+2z-5=0\] và hai điểm \[A\left( -3;0;1 \right),\text{ }B\left( 1;-1;3 \right).\] Trong các đường thẳng đi qua \[A\] và song song với \[\left( P \right)\], đường thẳng mà khoảng cách từ \[B\] đến đường thẳng đó là nhỏ nhất có phương trình là.

 Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[(P):2x-y+z-10=0\] và đường thẳng \[d:\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-1}{-1}\]. Đường thẳng \[\Delta \] cắt (P) và d lần lượt tại hai điểm M và N sao cho \[A(1;3;2)\] là trung điểm của cạnh MN. Tính độ dài đoạn MN. 

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left( P \right):x + 2y + z - 4 = 0$ và đường thẳng $d:\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{3}.$ Viết phương trình đường thẳng $\Delta $ nằm trong mặt phẳng $\left( P \right),$ đồng thời cắt và vuông góc với đường thẳng d.

Trong không gian với hệ tọa độ Oxyz , cho đường thẳng \[\text{d}:\frac{x+1}{2}=\frac{y}{1}=\frac{z-2}{1},\] mặt phẳng $\left( P \right):x+y-2\text{z}+5=0$ và \[A(1;-1;2).\] Đường thẳng \[\Delta \]  cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN . Một vectơ chỉ phương của \[\Delta \] là:

Trong không gian $Oxyz$, cho điểm $M\left( 2;1;0 \right)$ và đường thẳng $\Delta $ có phương trình $\Delta :\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-1}$. Viết phương trình đường thẳng $d$ đi qua $M$, cắt và vuông góc với đường thẳng $\Delta $.

Trong không gian với hệ tọa độ Oxyz, cho điểm \[A\text{ }\left( 1;-6;1 \right)\] và mặt phẳng

\[\left( \text{ }P\text{ } \right):\text{ x}+y+7=0.\] Điểm B thay đổi thuộc Oz, điểm C thay đổi thuộc mặt phẳng (P). Biết rằng tam giác ABC có chu vi nhỏ nhất. Tọa độ điểm B là:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm $A\left( {1;2; - 1} \right),B\left( {2;1;1} \right),C\left( {0;1;2} \right).$ Gọi điểm $H\left( {x;y;z} \right)$ là trực tâm tam giác ABC. Giá trị của $S = a + y + z$ là

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( 2;0;0 \right);B\left( 0;3;0 \right);C\left( 0;0;4 \right).$ Gọi H là trực tâm tam giác ABC. Tìm phương trình tham số của đường thẳng OH.

Trong không gian \[Oxyz,\] cho hai điểm \[A\left( 1;\,2;\,1 \right),\,\,B\left( 2;\,-1;\,3 \right).\] Tìm điểm \[M\] trên mặt phẳng \[\left( Oxy \right)\] sao cho \[M{{A}^{2}}-2M{{B}^{2}}\] lớn nhất.

Trong không gian $Oxyz$ cho các điểm $A\left( 3;-4;0 \right),B\left( 0;2;4 \right),C\left( 4;2;1 \right)$. Tìm tọa độ điểm D trên trục $Ox$ sao cho $AD=BC$.

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( 0;0;-2 \right),B\left( 4;0;0 \right).$ Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left( P \right):x+2y+-8=0$ và ba điểm $A\left( 0;-1;0 \right), B\left( 2;3;0 \right), C\left( 0;-5;2 \right).$ Gọi $M\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ là điểm thuộc mặt phẳng $\left( P \right)$ sao cho $MA=MB=MC.$ Tổng $S={{x}_{0}}+{{y}_{0}}+{{z}_{0}}$ bằng:

Cho đường thẳng $\Delta :\frac{x+1}{2}=\frac{y}{3}=\frac{x+1}{-1}$ và hai điểm $A\left( 1;2;-1 \right),\,\,B\left( 3;-1;-5 \right)$. Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng $\Delta $ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\frac{x-1}{1}=\frac{y-2}{1}=\frac{z-1}{2},\]\[A(2;1;4)\]. Gọi \[H(a;b;c)\] là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính \[T={{a}^{3}}+{{b}^{3}}+{{c}^{3}}\].

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d và mặt cầu (S) lần lượt có

phương trình là: $d:\frac{x+3}{-1}=\frac{y}{2}=\frac{z+1}{2};\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+2z-18=0.$ Biết d cắt (S) tại hai điểm M, N thì độ dài đoạn MN là:

Trong không gian với hệ trục tọa độ $Oxyz,$ mặt phẳng $(P):2x-y-z+5=0$ tiếp xúc với mặt cầu $(S):{{(x-3)}^{2}}+{{(y-1)}^{2}}+{{(z+2)}^{2}}=24$ tại điểm $M(a\ ;\ b\ ;\ c).$ Tính giá trị biểu thức $T=a+b+c.$

 Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm \[A(1;2;-4),\]\[B(1;-3;1),\]\[C(2;2;3)\]. Tìm đường kính I của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy).

Trong không gian với hệ tọa độ Oxyz, cho \[A\left( 2;0;0 \right); M\left( 1;1;1 \right).\] Mặt phẳng (P) thay đổi qua AM cắt các tia Oy; Oz lần lượt tại B, C . Khi mặt phẳng (P) thay đổi thì diện tích tam giác ABC đạt giá trị nhỏ nhất bằng bao nhiêu ?

Trong không gian với hệ trục Oxyz, cho các điểm \[\overrightarrow{A}\left( -1;2;3 \right),\text{ }\overrightarrow{B}\left( 6;-5;8 \right)\] và \[\overrightarrow{OM}=a\overrightarrow{i}+b\overrightarrow{k}\] trong đó a, b là các số thực luôn thay đổi. Nếu $\left| \overrightarrow{MA}-2\overrightarrow{MB} \right|$ đạt giá trị nhỏ nhất thì giá trị của a − b bằng: