Câu 1: Trang 12 - sgk hình học 10
Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM>MB. Vẽ các vec tơ \[\overrightarrow{MA}+\overrightarrow{MB}\] và \[\overrightarrow{MA}-\overrightarrow{MB}\]
Hướng dẫn giải

Trên đoạn MA, lấy điểm C sao cho: \[\overrightarrow{AC}=\overrightarrow{MB}\] suy ra \[\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AC}\]
<=>\[\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}\]
Tương tự \[\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+(-\overrightarrow{MB})\]
<=>\[\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\]
Câu 2: Trang 12 - sgk hình học 10
Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh rằng: \[\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\]
Hướng dẫn giải
.png)
Vì ABCD là hình bình hành => \[\overrightarrow{BA}=-\overrightarrow{DC}\]
=>\[\overrightarrow{BA}+\overrightarrow{DC}=\vec{0}\]
Mặt khác \[\overrightarrow{MA}+\overrightarrow{MC}=(\overrightarrow{MB}+\overrightarrow{BA})+(\overrightarrow{MD}+\overrightarrow{DC})\]
\[\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{BA}+\overrightarrow{DC}\]
\[\Leftrightarrow \overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\] (đpcm)
Câu 3: Trang 12 - sgk hình học 10
Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
a) \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\vec{0}\]
b) \[\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\]
Hướng dẫn giải
a) Theo quy tắc 3 điểm của tổng vec tơ, ta có \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\] ; \[\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{CA}\]
Như vậy
\[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\]\[=(\overrightarrow{AB}+\overrightarrow{BC})+(\overrightarrow{CD}+\overrightarrow{DA})\]\[=\overrightarrow{AC}+\overrightarrow{CA}\]
Mà \[\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{AA}=\vec{0}\]
Vậy \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\vec{0}\]
b) Theo quy tắc 3 điểm của hiệu vec tơ, ta có
\[\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}\](1)
\[\overrightarrow{CB}-\overrightarrow{CD}=\overrightarrow{DB}\] (2)
Từ (1) và (2) suy ra \[\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\]
Câu 4: Trang 12 - sgk hình học 10
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành: ABIJ, BCPQ, CARS.
Chứng minh rằng: \[\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\vec{0}.\]
Hướng dẫn giải
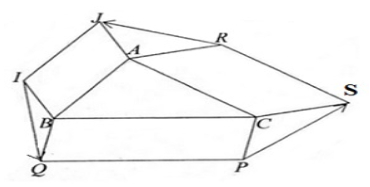
Ta có: \[\overrightarrow{AJ}=\overrightarrow{BI}=-\overrightarrow{IB}\]
\[\overrightarrow{CS}=-\overrightarrow{RA}\]
\[\overrightarrow{PC}=-\overrightarrow{BQ}\]
\[=>\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}\]
=\[(\overrightarrow{RA}+\overrightarrow{AJ})+(\overrightarrow{IB}+\overrightarrow{BQ})(\overrightarrow{PC}+\overrightarrow{CS})\]
=\[(\overrightarrow{RA}+\overrightarrow{-IB})+(\overrightarrow{IB}+\overrightarrow{-PC})+(\overrightarrow{PC}+\overrightarrow{-RA})\]
=\[(\overrightarrow{IB}+\overrightarrow{-IB})+(\overrightarrow{PC}+\overrightarrow{-PC})+(\overrightarrow{RA}+\overrightarrow{-RA})=\vec{0}\] ( đpcm )
Câu 5: Trang 12 - sgk hình học 10
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ \[\overrightarrow{AB}+\overrightarrow{BC}\] và \[\overrightarrow{AB}-\overrightarrow{BC}\]
Hướng dẫn giải
.png)
Ta có : \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
Suy ra \[\left| \overrightarrow{AB}+\overrightarrow{BC} \right|=AC=a\]
Kẻ \[\overrightarrow{AD}=\overrightarrow{BC}\]
=>\[\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}\]
Gọi I là giao điểm của AC và BD.
Mà ABCD là hình thoi => I là trung điểm BD và vuông tại I.
=>\[BI=AB\sin A=a\sin {{60}^{{}^\circ }}=\frac{a\sqrt{3}}{2}\]
=>\[BD=2BI=a\sqrt{3}\]
=>\[\left| \overrightarrow{AB}-\overrightarrow{BC} \right|=a\sqrt{3}\]
Câu 6: Trang 12 - sgk hình học 10
Cho hình bình hành ABCD có tâm O. Chứng minh rằng:
a) \[\overrightarrow{CO}-\overrightarrow{OB}=\overrightarrow{BA}\]
b) \[\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{DB}\]
c) \[\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{OD}-\overrightarrow{OC}\]
d) \[\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}\]
Hướng dẫn giải
.png)
a) Ta có: \[\overrightarrow{CO}=\overrightarrow{OA}\]\[\Rightarrow \overrightarrow{CO}-\overrightarrow{OB}=\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}.\]
b) Ta có: \[\overrightarrow{BC}=\overrightarrow{AD}\]\[\Rightarrow \overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}.\]
Mà \[\overrightarrow{BA}=\overrightarrow{CD}\]\[\Rightarrow \overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{OD}-\overrightarrow{OC}.\]
.png)
d) Ta có: \[\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{DC}\]\[=\overrightarrow{BA}+\overrightarrow{AB}=\vec{0}.\]
Câu 7: Trang 12 - sgk hình học 10
Cho vectơ a, b là hai vectơ khác vectơ 0. Khi nào có đẳng thức:
a) \[\left| \vec{a}+\vec{b} \right|=\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\]
b) \[\left| \vec{a}+\vec{b} \right|=\left| \vec{a}-\vec{b} \right|\]
Hướng dẫn giải
a) Để \[\left| \vec{a}+\vec{b} \right|=\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\] xảy ra
<=> \[\overrightarrow{a},\overrightarrow{b}\] cùng hướng.
b) Để \[\left| \vec{a}+\vec{b} \right|=\left| \vec{a}-\vec{b} \right|\] xảy ra
<=>\[\overrightarrow{a},\overrightarrow{b}\] vuông góc với nhau
Câu 8: Trang 12 - sgk hình học 10
Cho \[\left| \vec{a}+\vec{b} \right|=0\].
So sánh độ dài, phương và hướng của hai vectơ a và b.
Hướng dẫn giải
Từ \[\left| \vec{a}+\vec{b} \right|=0\], ta có \[\vec{a}+\vec{b}=\vec{0}\]\[\Rightarrow \vec{a}=-\vec{b}\]
Điều này chứng tỏ hai vectơ có cùng độ dài \[\left| {\vec{a}} \right|=\left| {\vec{b}} \right|\], cùng phương và ngược hướng.
Câu 9: Trang 12 - sgk hình học 10
Chứng minh rằng : \[\overrightarrow{AB}=\overrightarrow{CD}\] khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Hướng dẫn giải
Nếu \[\overrightarrow{AB}=\overrightarrow{CD}\] thì AB // CD
AB = CD
=> ABCD là hình bình hành.
Khi đó AD và BC có trung điểm trùng nhau.
Mặt khác: Nếu trung điểm AD và BC trùng nhau
=> Tứ giác ABCD là hình bình hành.
Suy ra \[\overrightarrow{AB}=\overrightarrow{CD}\] (đpcm )
Câu 10: Trang 12 - sgk hình học 10
Cho ba lực \[\overrightarrow{{{F}_{1}}}=\overrightarrow{MA},\overrightarrow{{{F}_{2}}}=\overrightarrow{MB}\] và \[\overrightarrow{{{F}_{3}}}=\overrightarrow{MC}\] cùng tác động
vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực \[\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}}\] đều là 100N và \[\widehat{AMB}={{60}^{0}}.\]
Tìm cường độ và hướng của lực F3.
Hướng dẫn giải
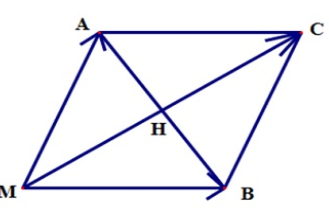
Theo bài ra: MA=MB=100N
\[\widehat{AMB}={{60}^{0}}.\]
\[\Rightarrow \vartriangle AMB~\] là tam giác đều.
\[MH=\frac{MA\sqrt{3}}{2}=50\sqrt{3}(N)\]
Vì AMBC là hình thoi => MC = 2MH.
=> \[MC=100\sqrt{3}(N)={{F}_{3}}\]
Vậy \[{{F}_{3}}=100\sqrt{3}(N)\]và có hướng là tia phân giác của \[\widehat{AMB}\]