Câu 1: Trang 17 - sgk hình học 10
Cho hình bình hành ABCD. Chứng minh rằng:
\[\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AC}\]
Hướng dẫn giải
Theo bài ra: ABCD là hình bình hành.
\[\Rightarrow \overrightarrow{AB}=\overrightarrow{DC}\]
\[\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{AC}\]
\[\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AC}=2\overrightarrow{AC}\] (đpcm)
Câu 2: Trang 17 - sgk hình học 10
Cho AK và BM là hai trung tuyến của tam giác ABC.Hãy phân tích các vectơ \[\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{AC}\] theo hai vectơ \[\vec{u}=\overrightarrow{AK},\vec{v}=\overrightarrow{BM}.\]
Hướng dẫn giải
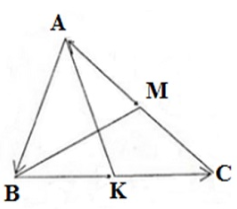
Vì AK là trung tuyến của ΔABC nên K là trung điểm của BC.
\[\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\] (1)
Vì BM là trung tuyến của ΔABC nên M là trung điểm của AC.
\[\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\] (2)
Từ (1),(2) => \[2\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{CB}=2(\overrightarrow{AK}-\overrightarrow{BM})\]
\[\Leftrightarrow 2\overrightarrow{AB}+\overrightarrow{AB}=2(\overrightarrow{AK}-\overrightarrow{BM})\]
\[\Leftrightarrow \]\[3\overrightarrow{AB}=2(\overrightarrow{AK}-\overrightarrow{BM})\]
\[\Leftrightarrow 3\overrightarrow{AB}=2(\vec{u}-\vec{v})\]
\[\Leftrightarrow \overrightarrow{AB}=\frac{2}{3}(\vec{u}-\vec{v})\]
Tương tự: \[\overrightarrow{BC}=\frac{2}{3}\vec{u}-\frac{4}{3}\vec{v}\]
\[\overrightarrow{CA}=-\frac{2}{3}(2\vec{u}+\vec{v})\]
Câu 3: Trang 17 - sgk hình học 10
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho \[\overrightarrow{MB}=3\overrightarrow{MC}\]
Hãy phân tích vec tơ \[\overrightarrow{AM}\] theo hai vec tơ \[\vec{u}=\overrightarrow{AB};\vec{v}=\overrightarrow{AC}.\]
Hướng dẫn giải
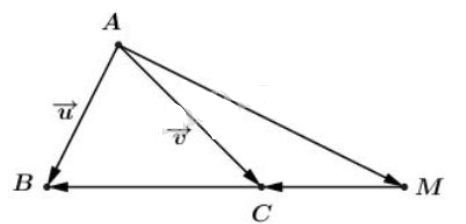
Trước hết ta có
\[\overrightarrow{MB}=3\overrightarrow{MC}\]
\[\Rightarrow \overrightarrow{MB}=3.(\overrightarrow{MB}+\overrightarrow{BC})\]
\[\Rightarrow \overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\]
\[\Rightarrow -2\overrightarrow{MB}=3\overrightarrow{BC}\]
\[\Rightarrow \overrightarrow{BM}=\frac{3}{2}\overrightarrow{BC}\]
Mà \[\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\] nên \[\overrightarrow{BM}=\frac{3}{2}(\overrightarrow{AC}-\overrightarrow{AB})\]
Theo quy tắc 3 điểm, ta có
\[\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\]
\[\;\;\;\;\;\;\;\;=\overrightarrow{AB}+\frac{3}{2}(\overrightarrow{AC}-\overrightarrow{AB})\]
\[\;\;\;\;\;\;\;\;\;=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AC}\]
Hay \[\text{ }\!\!~\!\!\text{ }\overrightarrow{AM}=-\frac{1}{2}\vec{u}+\frac{3}{2}\vec{v}\]
Câu 4: Trang 17 - sgk hình học 10
Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM.
Chứng minh rằng:
a) \[2\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}\]
b) \[2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=4\overrightarrow{OD}\] với O là điểm tùy ý.
Hướng dẫn giải
a)
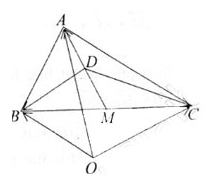
Vì M là trung điểm của BC nên ta có: \[\overrightarrow{DB}+\overrightarrow{DC}=2\overrightarrow{DM}\]
Mặt khác, do D là trung điểm của đoạn AM nên \[\overrightarrow{DM}=-\overrightarrow{DA}\]
Khi đó \[2\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=2\overrightarrow{DA}+2\overrightarrow{DM}\]\[=2\left( \overrightarrow{DA}+\overrightarrow{DM} \right)=\vec{0}\]
b) Ta có:
\[2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=4\overrightarrow{OD}\]
\[\Leftrightarrow 2\left( \overrightarrow{OA}-\overrightarrow{OD} \right)+\left( \overrightarrow{OB}-\overrightarrow{OD} \right)\]
\[+\left( \overrightarrow{OC}-\overrightarrow{OD} \right)=\vec{0}\]
\[\Leftrightarrow 2\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}\]
Vậy \[2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=4\overrightarrow{OD}\] với O là điểm tùy ý.
Câu 5: Trang 17 - sgk hình học 10
Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD.
Chứng minh rằng: \[2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{AD}\]
Hướng dẫn giải
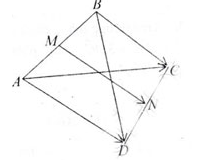
N là trung điểm của CD nên \[2\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{MD}\]
Theo quy tắc 3 điểm, ta có: \[\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AC}\]
\[\overrightarrow{MD}=\overrightarrow{MB}+\overrightarrow{BD}\]
\[\Rightarrow 2\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\]
\[=\left( \overrightarrow{MA}+\overrightarrow{MB} \right)+\overrightarrow{AC}+\overrightarrow{BD}\]\[=\overrightarrow{AC}+\overrightarrow{BD}\]
Chứng minh tương tự ta có \[2\overrightarrow{MN}=\overrightarrow{BC}+\overrightarrow{AD}.\]
Câu 6: Trang 17 - sgk hình học 10
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho: \[3\overrightarrow{KA}+2\overrightarrow{KB}=\vec{0}.\]
Hướng dẫn giải
Ta có: \[3\overrightarrow{KA}+2\overrightarrow{KB}=\vec{0}\]\[\Rightarrow 3\overrightarrow{KA}=-2\overrightarrow{KB}\]\[\Rightarrow \overrightarrow{KA}=-\frac{2}{3}\overrightarrow{KB}\]
Đẳng thức này chứng tỏ hi vec tơ \[\overrightarrow{KA},\overrightarrow{KB}\] là hai vecto ngược hướng, do đó K thuộc đoạn AB.
Ta lại có: \[\left| \overrightarrow{KA} \right|=\frac{2}{3}\left| \overrightarrow{KB} \right|\]\[\Rightarrow KA=\frac{2}{3}KB\]
Vậy K là trung điểm của AB theo tỉ số \[\frac{2}{3}\]

Câu 7: Trang 17 - sgk hình học 10
Cho tam giác ABC. Tìm điểm M sao cho: \[\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\vec{0}.\]
Hướng dẫn giải
Gọi D là trung điểm cạnh AB ta có
\[\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MD}\]
Đẳng thức đã cho trở thành:
\[2\overrightarrow{MD}+2\overrightarrow{MC}=\vec{0}\]
\[\Rightarrow \overrightarrow{MD}+\overrightarrow{MC}=\vec{0}\]
Đẳng thức này chứng tỏ M là trung điểm của CD.