Bài 1 (trang 62 SGK Hình học 10): Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
Lời giải:
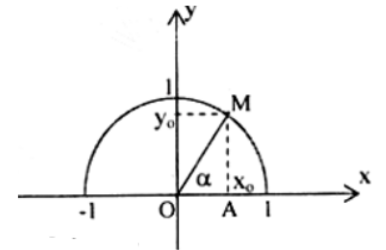
Với mỗi góc α (0o ≤ α ≤ 180o) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho xOM = α và giả sử M có tọa độ M(xo; yo). Khi đó:
- sin của góc α là yo, kí hiệu: sinα = yo
Khi α là góc nhọn, trong ΔOAM ta có:
\[\sin \alpha ={{y}_{0}}\]
\[\cos \alpha ={{x}_{0}}\]
\[\tan \alpha =\frac{{{y}_{0}}}{{{x}_{0}}}\]
\[\cot \alpha =\frac{{{x}_{0}}}{{{y}_{0}}}\]
Bài 2 (trang 62 SGK Hình học 10): Tại sao hai góc bù nhau lại có sin bằng nhau và cosin đối nhau?
Lời giải:
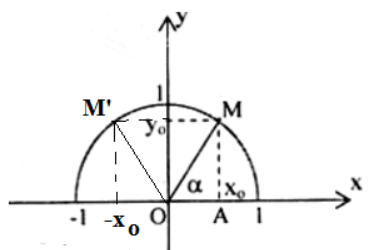
Gọi M(xo; yo) nằm trên nửa đường tròn đơn vị sao cho ∠xOM = α
Khi đó điểm M'(-xo; yo) trên nửa đường tròn đơn vị sao cho ∠xOM' = 180o - α (tức là ∠xOM' là bù với \[\widehat{xOM}\]= α
Do đó: sinα = yo = sin(180o - α)
cosα = xo = -(-xo) = -cos(180o - α)
Bài 3 (trang 62 SGK Hình học 10): Nhắc lại định nghĩa tích vô hướng của hai vectơ \[\vec{a}\] và \[\vec{b}\]. Tích vô hướng này với \[\left| {\vec{a}} \right|\] và \[\left| \overrightarrow{b} \right|\] không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào?
Lời giải:
Theo định nghĩa ta có: \[\vec{a}.\vec{b}=|\vec{a}|.|\vec{b}|.cos(\vec{a},\vec{b})\]
Vì \[|cos(\vec{a},\vec{b})|\le 1\] nên
+) \[\vec{a}.\vec{b}\] đạt giá trị lớn nhất \[|\vec{a}|.|\vec{b}|\] khi \[\cos (\vec{a},\vec{b})=1\Rightarrow (\vec{a},\vec{b})={{0}^{0}}\]
tức là \[\vec{a}\] và \[\vec{b}\] cùng hướng.
+) \[\vec{a}.\vec{b}\]đạt giá trị nhỏ nhất \[|\vec{a}|.|\vec{b}|\] khi \[\cos (\vec{a},\vec{b})=-1\Rightarrow (\vec{a},\vec{b})={{180}^{0}}\]
Tức là \[\vec{a}\] và \[\vec{b}\] ngược hướng.
Bài 4 (trang 62 SGK Hình học 10): Trong mặt phẳng Oxy cho \[\vec{a}=(-3;1)\] và vecto \[\vec{b}=(2;2)\]. Hãy tính tích vô hướng \[\vec{a}.\vec{b}.\]
Lời giải
Áp dụng công thức:
Với \[\vec{a}=({{a}_{1}};{{a}_{2}});\vec{b}=({{b}_{1}};{{b}_{2}})\]\[\Rightarrow \vec{a}.\vec{b}={{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}\]
Ta có \[\vec{a}.\vec{b}=(-3).2+1.2=-6+2=-4.\]
Bài 5 (trang 62 SGK Hình học 10): Hãy nhắc lại định lí côsin trong tam giác. Từ các hệ thức này hãy tính cosA, cosB, cosC theo các cạnh của tam giác.
Lời giải:
\[{{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.cosA\]
\[\Rightarrow \cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\]
\[{{b}^{2}}={{c}^{2}}+{{a}^{2}}-2ca.cosB\]
\[\Rightarrow cosB=\frac{{{c}^{2}}+{{a}^{2}}-{{b}^{2}}}{2ca}\]
\[{{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab.cosC\]
\[\Rightarrow cosC=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\]
Bài 6 (trang 62 SGK Hình học 10): Từ hệ thức a2 = b2 + c2 - 2bccosA trong tam giác, hãy suy ra định lý Pi-ta-go.
Lời giải:
Xét ΔABC vuông tại A, ta có:
a2 = b2 + c2 - 2bccosA
⇔a2 = b2 + c2 - 2bccos90o
⇔a2 = b2 + c2 (vì cos90o = 0)
Đây chính là định lí Pi-ta-go.
Bài 7 (trang 62 SGK Hình học 10): Chứng minh rằng với mọi tam giác ABC, ta có a = 2RsinA, b = 2RsinB, c = 2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác.
Lời giải:
Ta sử dụng định lí sin: \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
Từ đó suy ra: \[a=2R\sin A;b=2R\sin B;\] \[c=2R\sin C\]
Bài 8 (trang 62 SGK Hình học 10): Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Lời giải:
Theo hệ quả định lí côsin ta có: \[cosA=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\]
a) a2 < b2 + c2 ⇔ b2 + c2 - a2 > 0 ⇔ cosA > 0
⇔ A là góc nhọn
Vậy góc A nhọn khi và chỉ khi a2 < b2 + c2
b) a2 > b2 + c2 ⇔ b2 + c2 - a2 < 0 ⇔ cosA < 0
⇔ A là góc tù
Vậy góc A tù khi và chỉ khi a2 > b2 + c2
c) a2 = b2 + c2
Theo định lí Pitago suy ra A là góc vuông
Vậy góc A vuông khi và chỉ khi a2 = b2 + c2
(Lưu ý: ở phần c) bạn có thể làm như a) và b) để suy ra cosA = 0 cũng được)
Bài 9 (trang 62 SGK Hình học 10): Cho tam giác ABC có ∠A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Lời giải:
Sử dụng định lí sin, ta có: \[\frac{BC}{\sin A}=2R\]
\[\Rightarrow R=\frac{BC}{2\sin A}=\frac{6}{2.\sin {{60}^{0}}}=\frac{6}{\sqrt{3}}=2\sqrt{3}\]
Bài 10 (trang 62 SGK Hình học 10): Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác
Lời giải:
* Tính diện tích: Sử dụng công thức Hê-rông với:
\[p=\frac{12+16+20}{2}=24\]
\[S=\sqrt{24(24-12)(24-16)(24-20)}\]
\[\;\;\;=\sqrt{24.12.8.4}=96(dvdt)\]
* Tính \[{{h}_{a}}\], Ta có:
\[S=\frac{1}{2}a{{h}_{a}}\Leftrightarrow 96=\frac{1}{2}12.{{h}_{a}}\]
\[\Leftrightarrow 96=6.{{h}_{a}}\]
\[\Leftrightarrow {{h}_{a}}=\frac{96}{6}=16\]
* Tính R
Ta có: \[S=\frac{abc}{4R}\Leftrightarrow R=\frac{abc}{4S}=\frac{12.16.20}{4.96}=10\]
* Tính r
Ta có: \[S=p.r\Leftrightarrow r=\frac{S}{p}=\frac{96}{24}=4\]
* Tính ma. Ta có:
\[{{m}_{a}}^{2}=\frac{2({{b}^{2}}+{{c}^{2}})-{{a}^{2}}}{4}\]
\[\;\;\;\;\;\;\;=\frac{2({{16}^{2}}+{{20}^{2}})-{{12}^{2}}}{4}=292\]
\[\Leftrightarrow {{m}_{a}}^{2}=\sqrt{292}\approx 17,09\]
Bài 11 (trang 62 SGK Hình học 10): Trong tập hợp các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.
Lời giải:
Theo công thức tínhg diện tích tam giác, ta có: \[S=\frac{1}{2}ab\sin C\]
Vì a,b không đổi nên diện tích S lớn nhất khi sinC lớn nhất và vì −1≤sinC≤1 nên sinC lớn nhất khi
\[\sin C=1\Rightarrow \hat{C}={{90}^{0}}\]
Vậy trong tập hợp các tam giác có hai cạnh a và b thì tam giác vuông đỉnh C có diện tích lớn nhất.