Câu 1: Trang 40 - sgk hình học 10
Chứng minh rằng trong tam giác ABC có:
a) sinA=sin(B+C)
b) cosA=−cos(B+C)
Hướng dẫn giải
Trong một tam giác thì tổng các góc là 1800: \[\hat{A}+\hat{B}+\hat{C}={{180}^{0}}\]\[\Rightarrow \hat{A}={{180}^{0}}-(\hat{B}\]
\[A\] và \[(\hat{B}+\hat{C})\] là 2 góc bù nhau, do đó:
a) \[\sin A=\sin [{{180}^{0}}-(\hat{B}+\hat{C})]\]\[=\sin (B+C).\]
b) \[\cos A=\cos [{{180}^{0}}-(\hat{B}+\hat{C})]\] \[=-\cos (B+C).\]
Câu 2: Trang 40 - sgk hình học 10
Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử \[\widehat{AOH}=\alpha .\]
Tính AK và OK theo a và α.
Hướng dẫn giải
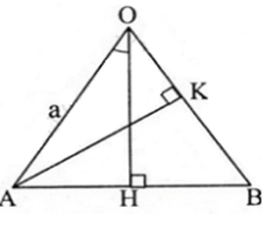
Ta có: OH là đường cao của tam giác cân AOB
=> OH là tia phân giác của \[\widehat{AOB}\]
Suy ra \[\widehat{AOB}=2\alpha \]
Xét △AOK vuông tại K, ta có: \[\frac{AK}{AO}=\sin 2\alpha =>AK=a\sin 2\alpha \]
Tương tự \[\frac{OK}{AO}=\cos 2\alpha =>OK=a\cos 2\alpha \]
Câu 3: Trang 40 - sgk hình học 10
Chứng minh rằng:
a) sin105∘=sin75∘
b) cos170∘=−cos10∘
c) cos122∘=−cos58∘
Hướng dẫn giải
Áp dụng tính chất lượng giác của hai góc bù nhau. ta có:
a) Ta có: 105∘=180∘−75∘
=> sin105∘=sin75∘
b) Ta có: 170∘=180∘−10∘
=> cos170∘=−cos10∘
c) Ta có: 122∘=180∘−58∘
=> cos122∘=−cos58∘
Câu 4: Trang 40 - sgk hình học 10
Chứng minh rằng với mọi góc α (0∘≤α≤180∘) ta đều có cos2α+sin2α=1.
Hướng dẫn giải
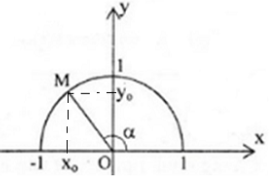
Từ M kẻ MP⊥Ox, MQ⊥Oy
Xét tam giác vuông OMP có:
\[sin\alpha =\frac{MP}{OM};\cos \alpha =\frac{OP}{OM}.\]
\[\Rightarrow {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =\frac{M{{P}^{2}}+O{{P}^{2}}}{O{{M}^{2}}}=\frac{O{{M}^{2}}}{O{{M}^{2}}}=1\]
Câu 5: Trang 40 - sgk hình học 10
Cho góc x, với \[\cos x=\frac{1}{3}.\] Tính giá trị của biểu thức: \[P=3{{\sin }^{2}}x+{{\cos }^{2}}x.\]
Hướng dẫn giải
Ta có: \[{{\sin }^{2}}x+{{\cos }^{2}}x=1\Rightarrow {{\sin }^{2}}x\]\[=1-{{\cos }^{2}}x.\]
Do đó \[P=3{{\sin }^{2}}x+{{\cos }^{2}}x\]\[=3(1-{{\cos }^{2}}x)+{{\cos }^{2}}x\]
\[=3-2{{\cos }^{2}}x=3-2.{{\left( \frac{1}{3} \right)}^{2}}=\frac{25}{9}.\]
Câu 6: Trang 40 - sgk hình học 10
Cho hình vuông ABCD. Tính:
\[\cos \left( \overrightarrow{AC},\overrightarrow{BA} \right),\sin \left( \overrightarrow{AC},\overrightarrow{BD} \right),\]\[\cos \left( \overrightarrow{AB},\overrightarrow{CD} \right).\]
Hướng dẫn giải
Ta có :
\[\cos \left( \overrightarrow{AC},\overrightarrow{BA} \right)=\cos \widehat{CAx}\]
\[\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\cos {{135}^{0}}=\frac{\sqrt{2}}{2},\]
\[\sin \left( \overrightarrow{AC},\overrightarrow{BD} \right)=\sin \widehat{COD}\]
\[\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\sin {{90}^{0}}=1,\]
\[\cos \left( \overrightarrow{AB},\overrightarrow{CD} \right)=\cos {{0}^{0}}=1.\]