Câu 1: Trang 7 - sgk hình học 10
Cho ba vectơ \[\vec{a},\vec{b},\vec{c}\] đều khác vec tơ \[\vec{0}\]. Các khẳng định sau đây đúng hay sai?
a) Nếu hai vectơ \[\vec{a}\], \[\vec{b}\] cùng phương với \[\vec{c}\] thì \[\vec{a}\], \[\vec{b}\] cùng phương.
b) Nếu \[\vec{a}\], \[\vec{b}\] cùng ngược hướng với \[\vec{c}\] thì \[\vec{a}\] và \[\vec{b}\] cùng hướng.
Hướng dẫn giải
Gọi theo thứ tự \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}},{{\text{ }\!\!\Delta\!\!\text{ }}_{2}},{{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\] là giá của các vectơ \[\vec{a},\vec{b},\vec{c}\]
a) \[\vec{a}\] cùng phương với \[\vec{c}\] \[\Rightarrow {{\text{ }\!\!\Delta\!\!\text{ }}_{1}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\] ( hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\]) (1)
\[\vec{b}\] cùng phương với \[\vec{c}\] \[\Rightarrow {{\text{ }\!\!\Delta\!\!\text{ }}_{2}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\] ( hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\]) (2)
Từ (1), (2) suy ra \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\] (hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\]), theo định nghĩa hai vectơ \[\vec{a}\], \[\vec{b}\] cùng phương
Vậy câu a) đúng
b) \[\vec{a}\] ngược hướng với \[\vec{c}\]\[\Rightarrow {{\text{ }\!\!\Delta\!\!\text{ }}_{1}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\] ( hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\]) (1)
\[\vec{b}\] ngược hướng với \[\vec{c}\]\[\Rightarrow {{\text{ }\!\!\Delta\!\!\text{ }}_{2}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\] ( hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{3}}\]) (2)
Từ (1), (2) suy ra \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}//{{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\] (hoặc \[{{\text{ }\!\!\Delta\!\!\text{ }}_{1}}\equiv {{\text{ }\!\!\Delta\!\!\text{ }}_{2}}\]), theo định nghĩa hai vectơ \[\vec{a}\], \[\vec{b}\] cùng phương
Mà \[\vec{a}\], \[\vec{b}\] cùng ngược hướng với \[\vec{c}\], Suy ra \[\vec{a}\] và \[\vec{b}\] cùng hướng.
Câu 2: Trang 7 - sgk hình học 10
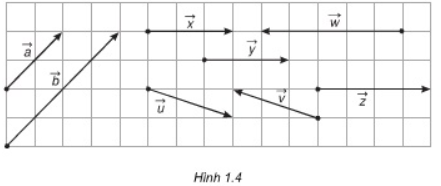
Trong hình 1.4, hãy chỉ ra các vector cùng phương, cùng hướng, ngược hướng và các vector bằng nhau.
Hướng dẫn giải
- Các vectơ cùng phương: \[\vec{a}\] và \[\vec{b}\]; \[\vec{x},\vec{y},\vec{z}\] ; \[\vec{u},\vec{v}\]
- Các vectơ cùng hướng: \[\vec{a}\] và \[\vec{b}\]; \[\vec{x},\vec{y},\vec{z}\]
- Các vectơ ngược hướng: \[\vec{u},\vec{v}\]; \[\vec{z}\] và \[\vec{w}\]; \[\vec{x}\] và \[\vec{w}\]
- Các vectơ bằng nhau: \[\vec{x}=\vec{y}\]
Câu 3: Trang 7 - sgk hình học 10
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \[\overrightarrow{AB}=\overrightarrow{CD}\]
Hướng dẫn giải
Ta chứng minh hai mệnh đề:
*) Khi \[\overrightarrow{AB}=\overrightarrow{DC}\] thì \[ABCD\] là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
\[\overrightarrow{AB}=\overrightarrow{DC}\Leftrightarrow \left| \overrightarrow{AB} \right|=\left| \overrightarrow{DC} \right|\] và \[\overrightarrow{AB},\overrightarrow{DC}\] cùng hướng.
Suy ra \[\overrightarrow{AB},\overrightarrow{DC}\] cùng phương, suy ra giá của chúng song song với nhau, hay \[AB//DC\]
Ta lại có \[\left| \overrightarrow{AB} \right|=\left| \overrightarrow{DC} \right|\] suy ra \[AB=DC\] (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
*) Khi ABCD là hình bình hành thì \[\overrightarrow{AB}=\overrightarrow{CD}\]
Khi ABCDABCD là hình bình hành thì AB//CD. Dễ thấy, từ đây ta suy ra hai vec tơ \[\overrightarrow{AB},\overrightarrow{DC}\] cùng hướng (3)
Mặt khác AB=CD suy ra \[\left| \overrightarrow{AB} \right|=\left| \overrightarrow{DC} \right|\] (4)
Từ (3) và (4) suy ra \[\overrightarrow{AB}=\overrightarrow{CD}\]
Như vậy tứ giác ABCD là hình bình hành khi và chỉ khi \[\overrightarrow{AB}=\overrightarrow{CD}\]
Câu 4: Trang 7 - sgk hình học 10
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ 0 và cùng phương với vectơ OA.
b) Tìm các vectơ bằng vectơ AB.
Hướng dẫn giải
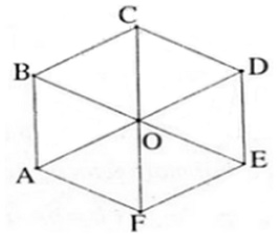
a) Các vectơ khác \[\overrightarrow{0}\] và cùng phương với \[\overrightarrow{~OA}\] là:
\[\overrightarrow{CB},\overrightarrow{BC},\overrightarrow{EF},\overrightarrow{FE},\overrightarrow{DO},\overrightarrow{OD},\overrightarrow{AO},\overrightarrow{DA},\overrightarrow{AD}\]
b) Các vectơ bằng \[\overrightarrow{AB}\] là: \[\overrightarrow{OC},\overrightarrow{ED},\overrightarrow{FO}\]