Câu 1: Trang 27 - sgk hình học 10
Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.
Hướng dẫn giải
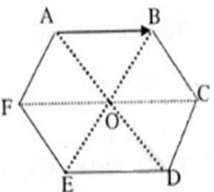
Các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác là:
\[\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\]
Câu 2 : Trang 27 - sgk hình học 10
Cho hai vectơ \[\vec{a}\] và \[\vec{b}\] đều khác \[\vec{0}\] . Các khẳng định sau đúng hay sai?
a) A. Hai vectơ \[\vec{a}\] và \[\vec{b}\] cùng hướng thì cùng phương.
B. Hai vectơ \[\vec{a}\] và k\[\vec{b}\] cùng phương.
C. Hai vectơ \[\vec{a}\] và (-2)\[\vec{a}\] cùng hướng.
D. Hai vectưo \[\vec{a}\] và \[\vec{b}\] ngược hướng với vectơ thứ ba khác \[\vec{0}\] thì cùng phương.
Hướng dẫn giải
a) Đúng, vì ta chỉ xét các vectơ cùng hướng hay ngược hướng khi các vectơ này cùng phương.
b) Đúng (theo định nghĩa tích của một số với một vectơ)
c) Sai, \[\vec{a}\] và (-2)\[\vec{a}\] là hai vectơ ngược hướng
d) Đúng vì \[\vec{a}\uparrow \downarrow \vec{c},\;\;\vec{b}\uparrow \downarrow \vec{c}\Rightarrow \vec{a}\uparrow \uparrow \vec{b}.\]
Câu 3: Trang 27 - sgk hình học 10
Tứ giác ABCD là hình gì nếu \[\overrightarrow{AB}=\overrightarrow{DC}\] và \[\left| \overrightarrow{AB} \right|=\left| \overrightarrow{BC} \right|\]
Hướng dẫn giải
Ta có: \[\overrightarrow{AB}=\overrightarrow{DC}\] suy ra \[AB//DC\]và AB=DC do đó ABCD là hình bình hành .
\[|\overrightarrow{AB}|=|\overrightarrow{BC}|\] suy ra AB=BC, hình bình hành ABCDcó 2 cạnh liên tiếp bằng nhau do đó ABCD là hình thoi (theo dấu hiệu nhận biết hình thoi).
Câu 4: Trang 27 - sgk hình học 10
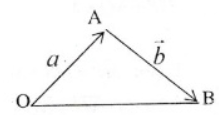
Chứng minh rằng \[|\vec{a}+\vec{b}|\le |\vec{a}|+|\overrightarrow{b|}.\]
Hướng dẫn giải
TH1: Khi vecto a, b cùng phương
\[\Rightarrow \vec{a}=k\vec{b}\]
\[\left| {\vec{a}} \right|=k\left| {\vec{b}} \right|\]
\[\left| \vec{a}+\vec{b} \right|\le \left| {\vec{a}} \right|+\left| {\vec{b}} \right|\](đpcm)
TH2: Khi vecto a, b không cùng phương
Từ hình vẽ \[|\vec{a}+\vec{b}|\le |\vec{a}|+|\overrightarrow{b|}.\](đpcm)
Câu 5: Trang 27 - sgk hình học 10
Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:
a) \[\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}\]
b) \[\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{OA}\]
c) \[\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}\]
Hướng dẫn giải
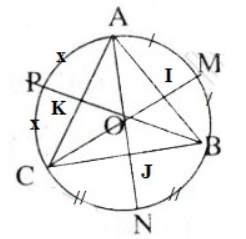
a) Nối OC và kéo dài cắt đường tròn tại điểm M
Dễ thấy, tam giác OAM là tam giác đều và OAMB là hình bình hành, cho ta: \[\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OM}\]
b) Nối OB và kéo dài cắt đường tròn tại điểm P
Tương tự như trên ta có:
\[\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{OA}\]
c) Nối OA và kéo dài cắt đường tròn tại điểm N
Tương tự như trên ta có:
\[\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}\]
Câu 6: Trang 27 - sgk hình học 10
Cho tam giác đều ABC có cạnh bằng a. Tính:
a) \[|\overrightarrow{AB}+\overrightarrow{AC}|\]
b) \[|\overrightarrow{AB}-\overrightarrow{AC}|\]
Hướng dẫn giải
a) Từ A vẽ đường cao AH, ta có: \[\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AH}\]
mà \[\overrightarrow{AH}=A\frac{\sqrt{3}}{2}\]
suy ra \[\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2\frac{a\sqrt{3}}{2}=a\sqrt{3}\]
b) Theo bài ra: \[|\overrightarrow{AB}-\overrightarrow{AC}|\]=\[\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\]
\[\Rightarrow \left| \overrightarrow{AB}-\overrightarrow{AC} \right|=\overrightarrow{CB}=a\]