Giải bài tập trang 49, 50 SGK Đại số 10 chương 2 Bài 3: Hàm số bậc hai

Giải bài tập trang 49, 50 SGK Đại số 10 chương 2

Bài 3: Hàm số bậc hai

Giải câu hỏi 1 trang 42 SGK Đại số 10

Nhắc lại các kết quả đã biết về đồ thị của hàm số y = ax².

Lời giải chi tiết

Đồ thị hàm số y = ax² là một parabol:

+ Nằm phía trên trục hoành nếu a > 0 và nhận điểm O(0;0) làm điểm thấp nhất.

+ Nằm phía dưới trục hoành nếu a < 0 và nhận điểm O(0;0) làm điểm cao nhất.

Giải câu hỏi 2 trang 42 SGK Đại số 10.

Vẽ parabol $y=-2{{x}^{2}}+x+3$

Lời giải chi tiết

Đỉnh I$({1 \over 4};\,{{28} \over 5})$

Trục đối xứng là đường thẳng x = ${1 \over 4}$

Giao điểm với trục Oy là điểm (0;3)

Giao điểm với trục Ox là điểm (${3 \over 2}$;0) và (-1;0)

Bài 1. (Trang 49 SGK Đại số 10 chương 2)

Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

a) $y = {x^2} - 3x + 2$;

b) $y=-2{{x}^{2}}+4x-3;$

c) $y= {x^2} - 2x$;

d) $y=-{{x}^{2}}+4.$

Lời giải chi tiết

a) $y = {x^2} - 3x + 2$.

Hệ số: $a = 1, b = - 3, c = 2$.

Hoành độ đỉnh $x_1$= $-\frac{b}{2a}=\frac{3}{2}.$

Tung độ đỉnh $y_1$ = $-\frac{\Delta }{4a}=\frac{4.2.1-(-3)^{2}}{4.1}=-\frac{1}{4}.$

Vậy đỉnh parabol là $I(\frac{3}{2};-\frac{1}{4})$.

Giao điểm của parabol với trục tung là $A(0; 2)$.
Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:

${{x}^{2}}-3x+2=0$

Vậy các giao điểm của parabol với trục hoành là $B(1; 0)$ và $C(2; 0)$.

b) $y=-2{{x}^{2}}+4x-3$

Hệ số: $a=-2;b=4;c=-3$

Hoành độ đỉnh $x_1$= $-\frac{b}{2a}=1$

Tung độ đỉnh $y_1$ = $-\frac{\Delta }{4a}=\frac{4.(-2).(-3)-4^{2}}{4.(-2)}=-1.$

Vậy đỉnh parabol là $I(1;-1)$.

Giao điểm với trục tung $A(0;- 3)$.

Phương trình $- 2x^2+ 4x - 3 = 0$ vô nghiệm. Không có giao điểm của parabol với trục hoành.

c) $y= {x^2} - 2x$

Hệ số: $a = 1; b = -2; c = 0$

Hoành độ đỉnh $x_1$= $-\frac{b}{2a}=1$

Tung độ đỉnh: $y_1$ = $-\frac{\Delta }{4a}=-1.$

Đỉnh $I(1;- 1)$.

Giao điểm của đồ thị với trục tung là: $A(0; 0)$

Các giao điểm với trục hoành là: $A(0; 0), B(2; 0)$.

d) $y=-{{x}^{2}}+4$

Hệ số: $a = - 1; b = 0; c = 4$

Hoành độ đỉnh $x_1$= $-\frac{b}{2a}=0$

Tung độ đỉnh: $y_1$ = $-\frac{\Delta }{4a}=4.$

Đỉnh $I(0;4)$.

Giao điểm của đồ thị với trục tung là: $A(0; 4)$

Các giao điểm với trục hoành là: $A(-2; 0), B(2; 0)$.

Bài 2. (Trang 49 SGK Đại số 10 chương 2)

Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) y = 3x²– 4x + 1; b) y = -3x² + 2x – 1;

c) y = 4x²– 4x + 1; d) y = -x² + 4x – 4;

e) y = 2x²+ x + 1; f) y = -x² + x – 1.

Lời giải chi tiết

a) $y=3{{x}^{2}}-4x+1$

Bảng biến thiên:

Đồ thị:

- Đỉnh: $I\left( {{2 \over 3}; - {1 \over 3}} \right)$

- Trục đối xứng: $x = {2 \over 3}$

- Giao điểm với trục tung $A(0; 1)$

- Giao điểm với trục hoành $B\left( {{1 \over 3};0} \right)$, $C(1; 0)$.

b) $y=-3{{x}^{2}}+2x-1$

Bảng biến thiên:

Vẽ đồ thị:

- Đỉnh $I\left( {{1 \over 3}; - {2 \over 3}} \right)$, trục đối xứng: $x = {1 \over 3}$

- Giao điểm với trục tung $A(0;- 1)$.

- Giao điểm với trục hoành: không có.

Ta xác định thêm điểm phụ: $B(1;- 2)$, $C(1;- 6)$.

c) \[y=4{{x}^{2}}-4x+1.\]

Lập bảng biến thiên và vẽ tương tự câu a, b.

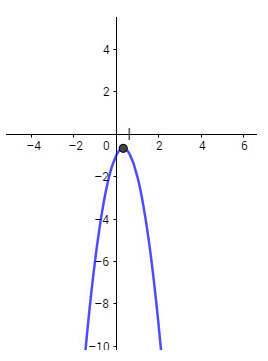
d) $y=-{{x}^{2}}+4x-4=-{{(x-2)}^{2}}$

Bảng biến thiên:

Cách vẽ đồ thị:

Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:

+ Vẽ đồ thị $(P)$ của hàm số $y = - x^2$^.

+ Tịnh tiến $(P)$ song song với $Ox$ sang phải $2$ đơn vị được $(P₁)$ là đồ thị cần vẽ.

e) $y=2{{x}^{2}}+x+1$

- Đỉnh $I\left( {{{ - 1} \over 4};{{ - 7} \over 8}} \right)$

- Trục đối xứng : $x = {{ - 1} \over 4}$

- Giao $Ox$: Đồ thị không giao với trục hoành

- Giao $Oy$: Giao với trục tung tại điểm $(0;1)$

Bảng biến thiên:

Vẽ đồ thị theo bảng sau:

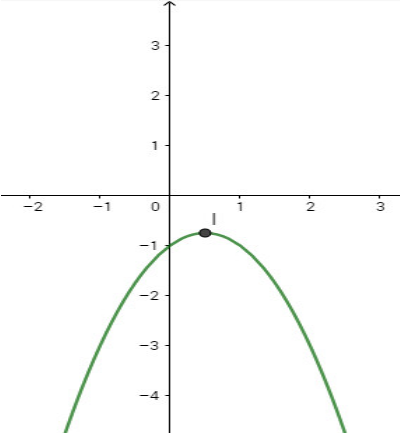
f) $y = - x^2+ x - 1$.

- Đỉnh $I\left( {{1 \over 2};{{ - 3} \over 4}} \right)$

- Trục đối xứng : $x = {1 \over 2}$

- Giao Ox: Đồ thị không giao với trục hoành

- Giao Oy: Giao với trục tung tại điểm $(0;-1)$

Bảng biến thiên:

Vẽ đồ thị theo bảng sau:

Bài 3 trang 49 sgk đại số 10

Xác định parabol $y = ax^2+ bx + 2$, biết rằng parabol đó:

a) Đi qua hai điểm $M(1; 5)$ và $N(- 2; 8)$;

b) Đi qua hai điểm $A(3;- 4)$ và có trục đối xứng là $x=-\frac{3}{2}.$

c) Có đỉnh là $I(2;- 2)$;

d) Đi qua điểm $B(- 1; 6)$ và tung độ của đỉnh là $-\frac{1}{4}.$

Lời giải chi tiết

a) Vì parabol đi qua $M(1; 5)$ nên tọa độ của $M$ là nghiệm đúng phương trình của parabol:

$5=a{{.1}^{2}}+b.1+2$.

Tương tự, với $N(- 2; 8)$ ta có:

$8=a.{{(-2)}^{2}}+b.(-2)+2$

Giải hệ phương trình: $\left\{\begin{matrix} a+b+2=5\\ 4a-2b+2=8 \end{matrix}\right.$

ta được $a = 2, b = 1$.

Parabol có phương trình là: $y = 2x^2 + x + 2$.

b) Vì parabol đi qua hai điểm $A(3;- 4)$ nên tọa độ $A$ là nghiệm đúng phương trình của parabol:

$a(3)^{2}+b.3+2=-4$

Parabol có trục đối xứng là $x=-\frac{3}{2}$ nên ta có:

$-\frac{b}{2a}=-\frac{3}{2}$

Giải hệ phương trình: $\left\{\begin{matrix} -\frac{b}{2a}=-\frac{3}{2}\\a(3)^{2}+b.3+2=-4 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-\frac{1}{3}\\ b=-1 \end{matrix}\right.$

Phương trình parabol cần tìm là: $y = -\frac{1}{3} x^2- x + 2$.

c) Parabol có đỉnh $I(2;- 2)$ do đó tọa độ $I$ là nghiệm đúng phương trình của parabol:

$a.2^2+b.2+2=-2$

Parabol có đỉnh $I(2;- 2)$ nên parabol có trục đối xứng là: $x=2$ do đó:

$-\frac{b}{2a}=2$

Giải hệ phương trình: $\left\{\begin{matrix} -\frac{b}{2a}=2\\a.2^2+b.2+2=-2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-4 \end{matrix}\right.$

Phương trình parabol cần tìm là: $y = x^2- 4x + 2$.

d) Vì parabol đi qua điểm $B(- 1; 6)$ nên tọa độ $B$ là nghiệm đúng phương trình của parabol:

$a(-1)^{2}+b(-1)+2=6$

Parabol có tung độ của đỉnh là $-\frac{1}{4}$ nên ta có:

$\frac{8a-b^{2}}{4a}=-\frac{1}{4} $

Giải hệ phương trình ta được:

$\left\{\begin{matrix} a(-1)^{2}+b(-1)+2=6\\ \frac{8a-b^{2}}{4a}=-\frac{1}{4} \end{matrix}\right.\Leftrightarrow \begin{bmatrix} \left\{\begin{matrix} a=16\\ b=12 \end{matrix}\right.\\ \left\{\begin{matrix} a=1\\ b=-3 \end{matrix}\right. \end{bmatrix}$

Phương trình parabol cần tìm là: $y = 16x^2+ 12x + 2$ hoặc $y = x^2- 3x + 2$.

Bài 4 trang 50 sgk đại số 10

Xác định $a, b, c$, biết parabol $y = ax^2+ bx + c$ đi qua điểm $A(8; 0)$ và có đỉnh $I(6; - 12)$.

Giải

Parabol đi qua điểm $A(8; 0)$ nên tọa độ điểm $A$ là nghiệm đúng phương trình của parabol ta có:

$a.8^2+b.8+c=0$

Parabol có đỉnh $I(6; - 12)$ nên ta có:

$-\frac{b}{2a}=6$

$\frac{4ac-b^{2}}{4a} =-12 $

Ta có hệ phương trình: $\left\{\begin{matrix} a(8)^{2}+b(8)+c=0\\ -\frac{b}{2a} =6 \\\frac{4ac-b^{2}}{4a} =-12 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=3\\ b=-36 \\ c=96 \end{matrix}\right.$

Phương trình parabol cần tìm là: $y = 3x^2- 36x + 96$.