Câu 1: Trang 26 - sgk hình học 10
Trên trục \[(0;\vec{e})\] cho các điểm A, B, M, N có tọa độ lần lượt là -1, 2, 3, -2.
a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục.
b) Tính độ dài đại số của \[\overrightarrow{AB}\] và \[\overrightarrow{MN}\]
Từ đó suy ra hai vectơ \[\overrightarrow{AB}\] và \[\overrightarrow{MN}\] ngược hướng.
Hướng dẫn giải
a) Biểu diễn các điểm trên trục:

\[b)\;\overrightarrow{AB}={{x}_{B}}-{{x}_{A}}=2-\left( -1 \right)=3.\]
\[\overrightarrow{MN}={{x}_{N}}-{{x}_{M}}=-2-3=-5.\]
Từ đây ta có \[\overrightarrow{AB}=3\vec{e};\overrightarrow{MN}=-5\vec{e}\]và suy ra \[\overrightarrow{AB}=-\frac{3}{5}\overrightarrow{MN}\]
Suy ra hai vectơ \[\overrightarrow{AB}\] và \[\overrightarrow{MN}\] ngược hướng.
Câu 2: Trang 26 - sgk hình học 10
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?
a) \[\vec{a}=(-3;0)\] và \[\vec{i}=(1;0)\] là hai vectơ ngược hướng.
a) \[\vec{a}=(3;4)\] và \[\vec{i}=(-3;-4)\] là hai vectơ đối nhau.
c) \[\vec{a}=(5;3)\] và \[\vec{i}=(3;5)\] là hai vectơ đối nhau.
d) Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Hướng dẫn giải
a) Ta có: \[\vec{a}=-3\vec{i}\Rightarrow \vec{a},\;\vec{i}\] là hai vecto ngược hướng.
Vậy a) đúng.
b) Ta có: \[\vec{a}=-\vec{i}\Rightarrow \vec{a},\;\vec{i}\] là hai vecto đối của nhau.
Vậy b) đúng.
c) Ta có:
.png)
không cùng phương.
Vậy c) sai.
d) Dựa vào định nghĩa hai vecto bằng nhau ta thấy đáp án D đúng.
Câu 3: Trang 26 - sgk hình học 10
Tìm tọa độ của các vectơ sau:
a) \[\vec{a}=2\vec{i}.\]
b) \[\vec{b}=-3\vec{j}.\]
c) \[\vec{c}=3\vec{i}-4\vec{j}.\]
d) \[\vec{d}=0,2\vec{i}+\sqrt{3}\vec{j}.\]
Hướng dẫn giải
a) Ta có \[\vec{a}=2\vec{i}=2\vec{i}+0\vec{j}\] suy ra \[\vec{a}=(2;0)\]
Tương tự ta có:
b) \[\vec{b}=(0;-3)\]
c) \[\vec{c}=(3;-4)\]
d) \[\vec{d}=(0,2;\sqrt{3})\]
Câu 4: Trang 26 - sgk hình học 10
Trong mặt phẳng Oxy. Các khẳng định sau đúng hay sai?
a) Tọa độ của điểm A bằng tọa độ của vectơ OA;
b) Điểm A nằm trên trục hoành thì có tung độ bằng 0;
c) Điểm A nằm trên trục tung thì có hoành độ bằng 0;
d) Hoành độ và tung độ của điểm A bằng nhau khi và chỉ khi A nằm trên tia phân giác của góc phần tư thứ nhất.
Hướng dẫn giải
a) Đúng.
b) Đúng.
c) Đúng.
d) Đúng (vì phân giác góc phần tư thứ nhất có phương trình y = x
Câu 5: Trang 27 - sgk hình học 10
Trong mặt phẳng tọa độ Oxy cho điểm M\[({{x}_{0}};{{y}_{0}})\]
a) Tìm tọa độ của điểm A đối xứng với M qua trục Ox;
b) Tìm tọa độ của điểm B đối xứng với M qua trục Oy;
c) Tìm tọa độ của điểm C đối xứng với M gốc O.
Hướng dẫn giải
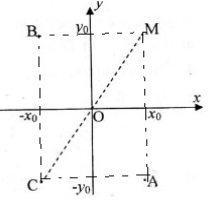
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
=> Tọa độ \[M({{x}_{0}};{{y}_{0}})\Rightarrow A({{x}_{0}};-{{y}_{0}})\]
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
\[M({{x}_{0}};{{y}_{0}})\Rightarrow B(-{{x}_{0}};{{y}_{0}})\]
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
\[M({{x}_{0}};{{y}_{0}})\Rightarrow C(-{{x}_{0}};-{{y}_{0}})\]
Câu 6: Trang 27 - sgk hình học 10
Cho hình bình hành ABCD có A(−1;−2),B(3;2),C(4;−1). Tìm tọa độ của đỉnh D.
Hướng dẫn giải
Gọi tọa độ của D\[({{x}_{0}};{{y}_{0}})\]
\[\overrightarrow{AD}=({{x}_{0}}+1;{{y}_{0}}+2)\]
\[\overrightarrow{BC}=(1;-3)\]
Mặt khác : ABCD là hình bình hành
Suy ra \[\overrightarrow{AD}=\overrightarrow{BC}\]
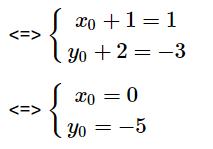
Vậy D(0;−5).
Câu 7: Trang 27 - sgk hình học 10
Các điểm A′(−4;1),B′(2;4),C′(2;−2) lần lượt là trung điểm các cạnh BC,CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC.
Chứng minh rằng trọng tâm của tam giác ABC và A'B'C' trùng nhau.
Hướng dẫn giải
Gọi A(x;y).
Ta có: \[\overrightarrow{A{C}'}=(2-x;-2-y)\]
\[\overrightarrow{{B}'{A}'}=(-6;-3)\]
Mà \[\overrightarrow{A{C}'}=\overrightarrow{{B}'{A}'}\]
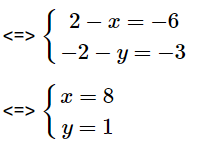
=> A(8;1)
Tương tự: B(−4;−5)
C=(−4;7)
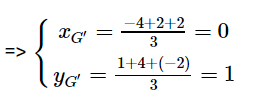
=> G′(0;1).
Vậy G ≡ G' hay hai trọng tâm của các tam giác ABC và A'B'C' trùng nhau (đpcm).
Câu 8: Trang 27 - sgk hình học 10
Cho vectơ \[\vec{a}=(2;-2)\], vectơ \[\vec{b}=(1;4)\]. Hãy phân tích vectơ \[\vec{c}=(5;0)\] theo hai vectơ \[\vec{a}\] và \[\vec{b}.\]
Hướng dẫn giải
Giả sử ta phân tích được \[\vec{c}\] theo \[\vec{a}\] và \[\vec{b}.\] tức là có hai số m, n để \[\vec{c}=m.\vec{a}+n.\vec{b}\]
Cho ta \[\vec{c}=(2m+n;-2m+4n)\]
Vì \[\vec{c}=(5;0)\] nên ta có hệ 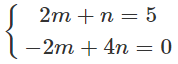
Giải hệ phương trình ta được m=2,n=1
vậy \[\vec{c}=2\vec{a}+\vec{b}\]