Bài 2: Hàm số y = ax + b
Giải câu hỏi 1 trang 40 SGK Đại số 10.
Vẽ đồ thị của các hàm số: y = 3x + 2; $y=-\frac{1}{2}x+5$
Lời giải chi tiết
.png)
Giải câu hỏi 2 trang 40 SGK Đại số 10.
Cho hàm số hằng y = 2.
Xác định giá trị của hàm số tại x = -2; -1; 0; 1; 2.
Biểu diễn các điểm (-2;2), (-1;2), (0;2), (1;2), (2;2) trên mặt phẳng tọa độ.
Nêu nhận xét về đồ thị của hàm số y = 2.
Lời giải chi tiết
+) Tại x = -2; -1; 0; 1; 2 thì y = 2
+) Đồ thị của hàm số y = 2 là đường thẳng song song với trục hoành và cắt trục hoành tại điểm (0; 2)
.png)
Giải bài 1 trang 41 SGK Đại số 10. Vẽ đồ thị hàm số.
Vẽ đồ thị hàm số:
a) $y=2x-3$;
b) $y=\sqrt{2}$;
c) $y=-\frac{3x}{2}+7$;
d) $y=\left| x \right|$.
Lời giải chi tiết
a) Đồ thị hàm số $y=2x-3$ là đường thẳng đi qua hai điểm $A\left( 0;-3 \right)$ và $B=\left( \frac{3}{2};0 \right)$
.png)
b) Đồ thị hàm số $y=\sqrt{2}$ là đường thẳng song song với trục hoành đi qua điểm $A\left( 0;\sqrt{2} \right)$
.png)
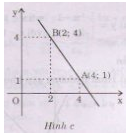
c) Đồ thị hàm số $y=-\frac{3x}{2}+7$ là đường thẳng. Bởi vì giao điểm của đồ thị với trục tung $P\left( 0;7 \right)$ với trục hoành $Q=\left( \frac{14}{3};0 \right)$ có tọa độ tương đối lớn nên ta có thể chọn các điểm thuộc đồ thị có tọa độ nhỏ hơn cho dễ vẽ. Chẳng hạn $A\left( 4;1 \right),B\left( 2;4 \right)$. Đồ thị là đường thẳng AB.
d)
.png)
Ta vẽ hai đường thẳng $y=x-1$ với $x\ge 0$ và đường thẳng $y=-x-1$ với $x<0$.
Đồ thị của (1) là nửa đường thẳng BA với B(0;-1) và A(1;0)
Đồ thị của (2) là nửa đưởng thẳng BA' với B(0;-1) và A' (-1;0)
Đồ thị của y = |x| - 1 gồm 2 tia Bt và Bt' (h.4)
.png)
Bài 2. (Trang 42 SGK Toán đại số 10)
Xác định a, b để đồ thị của hàm số y = ax + b đi qua các điểm.
a) $A\left( 0;3 \right)$ và $B=\left( \frac{3}{5};0 \right)$;
b) $A\left( 1;2 \right)$ và $B\left( 2;1 \right)$;
c) $A\left( 15;-3 \right)$ và $B\left( 21;-3 \right)$.
Lời giải chi tiết
a) Đồ thị hàm số $y=ax+b$ đi qua A, B nên tọa đồ của A, B thỏa mãn phương trình $y=ax+b$ ta được hệ phương trình: \(\left\{\begin{matrix} 3=a.0 + b\\ 0=a.\frac{3}{5}+b \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-5\\ b=3 \end{matrix}\right.\)
Vậy phương trình của đường thẳng đi qua $A\left( 0;3 \right)$ và $B=\left( \frac{3}{5};0 \right)$ là $y=-5x+3.$
b) Đồ thị hàm số $y=ax+b$ đi qua A, B nên tọa độ của A, B thỏa mãn phương trình $y=ax+b$ ta được hệ phương trình:
\(\left\{\begin{matrix} 2=a.1 + b\\ 1=a.2+b \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-1\\ b=3 \end{matrix}\right.\)
Phương trình đường thẳng cần tìm là: $y=-x+3$
c) Đồ thị hàm số $y=ax+b$ đi qua A, B nên tọa độ của A, B thỏa mãn phương trình $y=ax+b$ ta được hệ phương trình:
\(\left\{\begin{matrix} -3=a.15 + b\\ -3=a.21+b \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=0\\ b=-3 \end{matrix}\right.\)
Phương trình đường thẳng cần tìm là: $y=-3$.
Bài 3. (Trang 42 SGK Toán đại số 10)
Viết phương trình y = ax + b của đường thẳng:
a) Đi qua điểm A(4; 3), B(2;-1).
b) Đi qua điểm A(1;-1) và song song với Ox.
Hướng dẫn giải:
Các em có thể làm theo như bài 2 ở trên hoặc trình bày như dưới đây:
a) Phương trình đường thẳng (d) qua A(4; 3) và B(2;-1) có dạng tổng quát là y = ax + b, trong đó a, b là các hằng số cần xác định.
Vì A(4; 3) ∈ d nên ta có phương trình của (d), do đó ta có: 3 = a.4 + b.
Tương tự B(2;-1) ∈ d nên ta có: -1 = a.2 + b
Từ đó ta tìm được phương trình đường thẳng AB là: y = 2x – 5.
Phương trình đường thẳng AB là: y = 2x – 5.
b) Gợi ý: Δ đi qua a(1;-1) và song song với trục hoành nên phương trình của Δ có dạng: y = -1
Bài 4. (Trang 42 SGK Toán đại số 10)
Vẽ đồ thị các hàm số
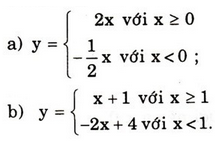
Hướng dẫn giải:

