Câu 1: Trang 45 - sgk hình học 10
Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng:
\[\overrightarrow{AB}.\overrightarrow{AC}\], \[\overrightarrow{AC}.\overrightarrow{CB}\]
Hướng dẫn giải
Ta có: \[\overrightarrow{AB}.\overrightarrow{AC}=\left| AB \right|.\left| AC \right|\cos (\overrightarrow{AB},\overrightarrow{AC})\]
\[\Leftrightarrow \overrightarrow{AB}.\overrightarrow{AC}=a.a.\cos {{90}^{{}^\circ }}=0\]
\[\overrightarrow{AB}.\overrightarrow{AC}=0\]
Tương tự: \[\overrightarrow{AC}.\overrightarrow{CB}=\left| AC \right|.\left| CB \right|.\cos (\overrightarrow{AC},\overrightarrow{CB})\]
\[\Leftrightarrow \overrightarrow{AC}.\overrightarrow{CB}=a.a\sqrt{2}.\cos {{135}^{{}^\circ }}=-{{a}^{2}}\]
Câu 2: Trang 45 - sgk hình học 10
Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng \[\overrightarrow{OA}.\overrightarrow{OB}\] trong hai trường hợp:
a) Điểm O nằm ngoài đoạn AB.
b) Điểm O nằm trong đoạn AB.
Hướng dẫn giải
a) \[\overrightarrow{OA}.\overrightarrow{OB}=\left| \overrightarrow{OA} \right|.\left| \overrightarrow{OB} \right|\cos {{0}^{{}^\circ }}\]
suy ra \[\overrightarrow{OA}.\overrightarrow{OB}=a.b\]
b) Ta có: \[\overrightarrow{OA},\overrightarrow{OB}\] ngược hướng
\[(\overrightarrow{OA},\overrightarrow{OB})={{180}^{{}^\circ }}\]
\[\Rightarrow \cos (\overrightarrow{OA},\overrightarrow{OB})=-1\]
\[\Rightarrow \overrightarrow{OA}.\overrightarrow{OB}=-a.b\]
Câu 3: Trang 45 - sgk hình học 10
Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.
a) Chứng minh: \[\overrightarrow{AI}.\overrightarrow{AM}=\overrightarrow{AI}.\overrightarrow{AB}\] và \[\overrightarrow{BI}.\overrightarrow{BN}=\overrightarrow{BI}.\overrightarrow{BA}\]
b) Hãy dùng kết quả câu a) để tính \[\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{BI}.\overrightarrow{BN}\] theo R.
Hướng dẫn giải
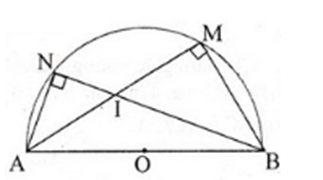
Ta có : \[\left( \overrightarrow{AI}.\overrightarrow{AB} \right)=\overrightarrow{AI}\left( \overrightarrow{AM}+\overrightarrow{MB} \right)\]\[=\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{AI}.\overrightarrow{MB}\]
Mặt khác \[\overrightarrow{AI}\bot \overrightarrow{MB}\] nên \[\overrightarrow{AI}.\overrightarrow{MB}=0\]
Từ đó \[\overrightarrow{AI}.\overrightarrow{AM}=\overrightarrow{AI}.\overrightarrow{AB}\]
Ta có \[\overrightarrow{BI}.\overrightarrow{BA}=\overrightarrow{BI}\left( \overrightarrow{BN}+\overrightarrow{NA} \right)\]\[=\overrightarrow{BI}.\overrightarrow{BN}+\overrightarrow{BI}.\overrightarrow{NA}\]
Mặt khác \[\overrightarrow{BI}\bot \overrightarrow{NA}\] nên \[\overrightarrow{BI}.\overrightarrow{NA}=0\]
Từ đó \[\overrightarrow{BI}.\overrightarrow{BN}=\overrightarrow{BI}.\overrightarrow{BA}\]
b) \[\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{BI}.\overrightarrow{BN}\]
\[=\overrightarrow{AI}.\overrightarrow{AB}+\overrightarrow{BI}.\overrightarrow{BA}\]
\[=\overrightarrow{AI}.\overrightarrow{AB}-\overrightarrow{BI}.\overrightarrow{AB}\]
\[=\overrightarrow{AB}\left( \overrightarrow{AI}-\overrightarrow{BI} \right)\]
\[=\overrightarrow{AB}.\overrightarrow{AB}={{\overrightarrow{AB}}^{2}}=4{{\text{R}}^{2}}\]
Câu 4: Trang 45 - sgk hình học 10
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(1; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Hướng dẫn giải
a) Gọi tọa độ D(x; 0).
Ta có: \[DA=\sqrt{{{(1-x)}^{2}}+{{3}^{2}}}=\sqrt{{{x}^{2}}-2x+10}\]
\[DB=\sqrt{{{(4-x)}^{2}}+{{2}^{2}}}=\sqrt{{{x}^{2}}-8x+20}\]
Mà DA=DB =>\[\sqrt{{{x}^{2}}-2x+10}=\sqrt{{{x}^{2}}-8x+20}\]
<=> \[6x=10<=>x=\frac{5}{3}\]
=>\[D(\frac{5}{3};0)\]
b) Ta có:\[O{{A}^{2}}={{1}^{2}}+{{3}^{2}}=10\]
\[\Rightarrow OA=\sqrt{10}\]
\[A{{B}^{2}}={{3}^{2}}+{{(-1)}^{2}}=10\]
Suy ra \[AB=\sqrt{10}\]
\[O{{B}^{2}}={{4}^{2}}+{{2}^{2}}=20\]
\[\Rightarrow OB=\sqrt{2}.\sqrt{10}\]
=> Chu vi ΔOAB là: \[OA+AB+OB=\sqrt{10}+\sqrt{10}+\sqrt{2}.\sqrt{10}=\sqrt{10}(2+\sqrt{2})\]
c) Ta có: \[O{{A}^{2}}+A{{B}^{2}}=20=O{{B}^{2}}\]=> ΔOAB vuông tại A <=> OA⊥AB
Diện tích ΔOAB là: \[\frac{1}{2}OA.OB=\frac{1}{2}\sqrt{10}\sqrt{10}=5\]
Câu 5: Trang 45 - sgk hình học 10
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a⃗ và b⃗ trong các trường hợp sau:
a) \[\overrightarrow{a}\] =(2;−3) và \[\overrightarrow{b}\]=(6;4)
b) \[\overrightarrow{a}\]=(3;2) và \[\overrightarrow{a}\] =(5;−1)
c) \[\overrightarrow{a}\] =(−2;−2\[\sqrt{3}\]) và \[\overrightarrow{b}\]=(3;\[\sqrt{3}\])
Hướng dẫn giải
a) \[\vec{a}.\vec{b}=2.6+\left( -3 \right).4=0\Rightarrow \vec{a}\bot \vec{b}\]hay \[\left( \vec{a},\vec{b} \right)={{90}^{0}}\]
b) \[\vec{a}.\vec{b}=3.5+2\left( -1 \right)=13\]
\[\left| {\vec{a}} \right|=\sqrt{9+4}=\sqrt{13},\]
\[\left| {\vec{b}} \right|=\sqrt{25+1}=\sqrt{26}.\]
\[\Rightarrow cos\left( \vec{a},\;\vec{b} \right)=\frac{13}{\sqrt{13}.\sqrt{26}}=\frac{\sqrt{2}}{2}.\]
\[\Rightarrow \left( \vec{a},\;\vec{b} \right)={{45}^{0}}.\]
c) \[\vec{a}.\vec{b}=-2.3+\left( -2\sqrt{3} \right).\sqrt{3}=-12\]
\[\left| {\vec{a}} \right|=\sqrt{4+12}=4,\]
\[\left| {\vec{b}} \right|=\sqrt{9+3}=2\sqrt{3}.\]
\[\Rightarrow cos\left( \vec{a},\;\vec{b} \right)=\frac{-12}{4.2\sqrt{3}}=\frac{-\sqrt{3}}{2}.\]
\[\Rightarrow \left( \vec{a},\;\vec{b} \right)={{150}^{0}}.\]
Câu 6: Trang 45 - sgk hình học 10
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
Hướng dẫn giải
Ta có: \[\overrightarrow{AB}=(1;7)\]; \[\overrightarrow{DC}=(1;7)\]
\[\Rightarrow \overrightarrow{AB}=\overrightarrow{DC}\Rightarrow ABCD\]là hình bình hành (1)
Ta có :
\[A{{B}^{2}}={{(8-7)}^{2}}+{{(4+3)}^{2}}=1+49\]\[\Rightarrow AB=5\sqrt{2}\]
\[\Rightarrow AB=5\sqrt{2}A{{D}^{2}}={{(0-7)}^{2}}+{{(-2+3)}^{2}}=49+1\]=50\[\Rightarrow AD=5\sqrt{2}\]
Suy ra AB=AD, kết hợp với (1) suy ra ABCD là hình thoi (2)
Mặt khác \[\overrightarrow{AB}=(1;7)\];\[\overrightarrow{AD}=(-7;1)\]
\[\overrightarrow{AB}.\overrightarrow{AD}=1.(-7)+7.1=0\]\[\Rightarrow \overrightarrow{AB}\bot \overrightarrow{AD}\](3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông.
Câu 7: Trang 45 - sgk hình học 10
Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
Hướng dẫn giải
Vì B đối xứng với A(-2; 1) qua O nên ta có: B(2; -1)
Gọi tọa độ C(x; 2).
Mà \[\overrightarrow{CA}=(-2-x;-1)\]
\[\overrightarrow{CB}=(2-x;-3)\]
Xét △ABC vuông tại C =>\[\overrightarrow{CA}.\overrightarrow{CB}=0\]
Suy ra \[-\left( 2\text{ }+\text{ }x \right)\left( 2\text{ }-\text{ }x \right)\text{ }+\text{ }3\text{ }=\text{ }0\]
\[\Leftrightarrow -4+{{x}^{2}}+3=0\]
\[\Leftrightarrow {{x}^{2}}=1<=>x=\text{ }\!\!\pm\!\!\text{ }1\]
Vậy C(1; 2) hay C(-1; 2).