Câu 1: Trang 59 - sgk hình học 10
Cho tam giác ABC vuông tại A, \[\hat{B}={{58}^{0}}\] và cạnh a = 72cm. Tính \[\hat{C}\], cạnh b và đường cao h.
Hướng dẫn giải
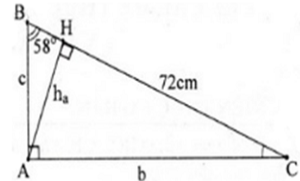
Ta có: \[\hat{C}={{90}^{{}^\circ }}-\hat{B}={{90}^{{}^\circ }}-{{58}^{{}^\circ }}={{32}^{{}^\circ }}\]
\[\Rightarrow b=BC.\sin {{58}^{{}^\circ }}=a.\sin {{58}^{{}^\circ }}=61,06(cm)\]
\[c=BC.\cos {{58}^{{}^\circ }}=a.\cos {{58}^{{}^\circ }}=38,15(cm)\]
\[\Rightarrow {{h}_{a}}=\frac{AB.AC}{BC}=\frac{c.b}{a}=\frac{38,15.61,06}{72}=32,35(cm)\]
Câu 2: Trang 59 - sgk hình học 10
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc \[\hat{A},\hat{B},\hat{C}\]
Hướng dẫn giải
Từ định lí cosin ta có: \[{{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.cosA.\]
Ta suy ra \[\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\]
\[=\frac{{{85}^{2}}+{{54}^{2}}-{{(52,1)}^{2}}}{2.85.54}\]
\[\Rightarrow \cos A\approx 0,8089\Rightarrow \hat{A}={{36}^{0}}\]
Tương tự , ta tính được \[\hat{B}\approx {{106}^{0}}{{28}^{\prime }}\]
\[\hat{C}\approx {{37}^{0}}{{32}^{\prime }}\]
Câu 3: Trang 59 - sgk hình học 10
Cho tam giác ABC có \[\hat{A}={{120}^{0}}\] , cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc \[\hat{B},\hat{C}\] của tam giác đó.
Hướng dẫn giải
Ta có
\[{{a}^{2}}={{8}^{2}}+{{5}^{2}}-2.8.5.cos{{120}^{0}}\]
\[\;\;\;\;=64+25+40=129\]
\[\Rightarrow a=\sqrt{129}\approx 11,36cm\]
Ta có thể tính góc B theo định lí cosin
\[\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}=\frac{129+25-64}{2.\sqrt{129}.5}\approx 0,7924\]
\[\Rightarrow \hat{B}={{37}^{0}}{{35}^{\prime }}\]
Ta cũng có thể tính góc B theo định lí sin :
\[\cos B=\frac{11,36}{\sin {{120}^{0}}}=\frac{8}{\sin B}\]\[\Rightarrow \sin B\approx 0,6085\]
\[\Rightarrow \hat{B}={{37}^{0}}{{35}^{\prime }}\]
Tổng ba góc trong một tam giác bằng 1800
\[\hat{C}={{180}^{0}}-(\hat{A}+\hat{B})={{180}^{0}}-{{120}^{0}}-{{37}^{0}}{{35}^{\prime }}\Rightarrow \hat{C}={{22}^{0}}{{25}^{\prime }}.\]
Câu 4: Trang 59 - sgk hình học 10
Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
Hướng dẫn giải
Ta có: \[2p=7+9+12\Rightarrow p=14\]
\[p-a=14-7=7\]
\[p-b=14-9=5\]
\[p-c=14-12=2\]
Áp dụng công thức Hêrong:
\[S=\sqrt{14.7.5.2}=\sqrt{{{2}^{2}}{{.7}^{2}}.5}=14\sqrt{5}\]
Câu 5: Trang 59 - sgk hình học 10
Cho tam giác ABC có \[\hat{A}={{120}^{0}}\]. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Hướng dẫn giải
\[B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB.AC.cosA\]
\[\Rightarrow B{{C}^{2}}={{m}^{2}}+{{n}^{2}}-2.m.n.\left( -\frac{1}{2} \right)\]
\[\Rightarrow B{{C}^{2}}={{m}^{2}}+{{n}^{2}}+m.n\]
\[\Rightarrow BC=\sqrt{{{m}^{2}}+{{n}^{2}}+m.n}.\]
Câu 6: Trang 59 - sgk hình học 10
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Hướng dẫn giải
a) Xét tổng \[{{a}^{2}}+{{b}^{2}}-{{c}^{2}}={{8}^{2}}+{{10}^{2}}-{{13}^{2}}=-5<0\]
Vậy tam giác ABC có góc C tù
\[\cos C=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\frac{-5}{160}\approx -0,3125\]
Suy ra \[\hat{C}={{91}^{0}}{{47}^{\prime }}\]
b) Áp dụng công thức tính đường trung tuyến, ta tính được:
\[A{{M}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{2}-\frac{{{a}^{2}}}{4}=\frac{{{10}^{2}}+{{13}^{2}}}{2}-\frac{{{8}^{2}}}{4}=118,5\]
Suy ra \[AM\approx 10,89cm.\]
Câu 7: Trang 59 - sgk hình học 10
Tính góc lớn nhất của tam giác ABC biết:
a) Các cạnh a = 3cm, b = 4cm và c = 6cm;
b) Các cạnh a = 40cm, b = 13cm, c = 37cm.
Hướng dẫn giải
a) Ta có: \[c>b>a\Rightarrow \hat{C}\] là góc lớn nhất của tam giác ABC.
\[\cos \hat{C}=\frac{9+16-36}{2.3.4}=\frac{-11}{24}\approx -0,4583\]
Suy ra \[\hat{C}={{117}^{0}}{{16}^{\prime }}.\]
b) Ta có: \[a>c>b\Rightarrow \hat{A}\] là góc lớn nhất của tam giác ABC.
\[\cos \hat{A}=\frac{{{13}^{2}}+{{37}^{2}}-{{40}^{2}}}{2.13.37}=\frac{-62}{702}\]
Suy ra \[\hat{A}={{93}^{0}}{{41}^{\prime }}.\]
Câu 8: Trang 59 - sgk hình học 10
Cho tam giác ABC biết cạnh \[a=137,5cm;\hat{B}={{83}^{0}},\hat{C}={{57}^{0}}.\] Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
Hướng dẫn giải
Ta có: \[\hat{A}={{180}^{0}}-(\hat{B}+\hat{C})={{40}^{0}}\]
Áp dụng định lí \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\] ta có
\[b=\frac{a\sin B}{\sin A}=\frac{137,5.\sin {{83}^{0}}}{\sin {{40}^{0}}}\approx 212,31cm.\]
\[c=\frac{a\sin C}{\sin A}=\frac{137,5.\sin {{57}^{0}}}{\sin {{40}^{0}}}\approx 179,40cm.\]
Câu 9: Trang 59 - sgk hình học 10
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n.
Chứng minh rằng: \[{{m}^{2}}+{{n}^{2}}=2({{a}^{2}}+{{b}^{2}})\]
Hướng dẫn giải
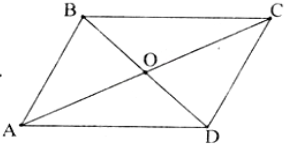
Gọi O là giao điểm của AC và BD.
Khi đó O là trung điểm của AC và BD, đồng thời BO là trung tuyến của ΔABC.
\[O{{A}^{2}}=\frac{A{{D}^{2}}+A{{B}^{2}}}{2}-\frac{B{{D}^{2}}}{4}\]
Thay \[OA=\frac{n}{2},AB=a,AD=BC=b\] và \[BD=m\] ta được
\[{{\left( \frac{n}{2} \right)}^{2}}=\frac{{{b}^{2}}+{{a}^{2}}}{2}-\frac{{{m}^{2}}}{4}\Rightarrow {{n}^{2}}=2{{b}^{2}}+2{{a}^{2}}-{{m}^{2}}\]
\[\Rightarrow {{m}^{2}}+{{n}^{2}}=2({{a}^{2}}+{{b}^{2}}).\]
Câu 10: Trang 60 - sgk hình học 10
Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các
góc \[\widehat{BPA}={{35}^{0}},\widehat{BQA}={{48}^{0}}.\]. Tính chiều cao của tháp.
Hướng dẫn giải
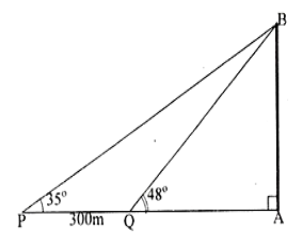
Ta có: \[\cot Q=\frac{AQ}{AB}\Rightarrow AQ=AB\cot {{48}^{0}}\]
Tương tự có: \[AP=AB\cot {{35}^{0}}\]
\[\Rightarrow QP=AP-AQ\]\[=AB(cot{{35}^{0}}-cot{{48}^{0}})\]
\[\Rightarrow AB=\frac{300}{\cot {{35}^{0}}-\cot {{48}^{0}}}\approx \frac{300}{1,4281-0,9004}\approx 568,457m.\]
Câu 11: Trang 60 - sgk hình học 10
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A1,B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được \[\widehat{D{{A}_{1}}{{C}_{1}}}={{49}^{0}}\] và \[\widehat{D{{B}_{1}}{{C}_{1}}}={{35}^{0}}.\]Tính chiều cao CD của tháp đó.
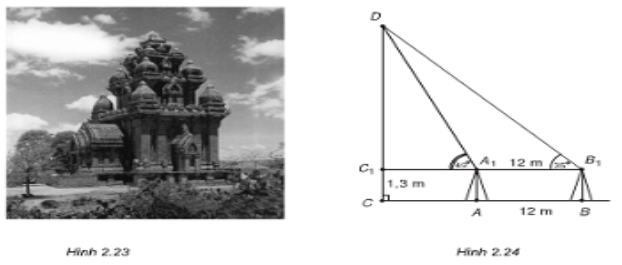
Hướng dẫn giải
Ta có: \[{{A}_{1}}{{B}_{1}}=Ab=12m.\]
Xét \[\text{ }\!\!\Delta\!\!\text{ }D{{C}_{1}}{{A}_{1}}\] có:\[{{C}_{1}}{{A}_{1}}={{C}_{1}}D.\cot {{49}^{0}}\]
Xét \[\text{ }\!\!\Delta\!\!\text{ }D{{C}_{1}}{{B}_{1}}\] có: \[{{C}_{1}}{{B}_{1}}={{C}_{1}}D.\cot {{35}^{0}}\]
Mà \[{{A}_{1}}{{B}_{1}}={{C}_{1}}{{B}_{1}}-{{C}_{1}}{{A}_{1}}={{C}_{1}}D.\cot {{35}^{0}}-{{C}_{1}}D.\cot {{49}^{0}}={{C}_{1}}D(\cot {{35}^{0}}-\cot {{49}^{0}}).\]
\[\Rightarrow {{C}_{1}}D=\frac{{{A}_{1}}{{B}_{1}}}{\cot {{35}^{0}}-\cot {{49}^{0}}}=\frac{12}{\cot {{35}^{0}}-\cot {{49}^{0}}}\approx 21,47m.\]
Vậy chiều cao CD của tháp là
\[DC=1,3+21,47=22,77m.\]