Bài 1 (trang 83 SGK Hình học 10): Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Lời giải
a) Ta có : \[-2a=-2\Rightarrow a=1\]
\[-2b=-2\Rightarrow b=1\Rightarrow I(1;1)\]
\[{{R}^{2}}={{a}^{2}}+{{b}^{2}}-c\]\[={{1}^{2}}+{{1}^{2}}-(-2)=4\Rightarrow R=\sqrt{4}=2\]
b) \[16{{x}^{2}}+16{{y}^{2}}+16x-8y-11=0\]
\[\Leftrightarrow {{x}^{2}}+{{y}^{2}}+x-\frac{1}{2}y-\frac{11}{16}=0\]
\[-2a=1\Rightarrow a=-\frac{1}{2}\]
\[-2b=-\frac{1}{2}\Rightarrow b=\frac{1}{4}\]
\[\Rightarrow I\left( -\frac{1}{2};\frac{1}{4} \right)\]
\[{{R}^{2}}={{a}^{2}}+{{b}^{2}}-c\]\[={{\left( -\frac{1}{2} \right)}^{2}}+{{\left( \frac{1}{4} \right)}^{2}}-\left( -\frac{11}{16} \right)=1\Rightarrow R=\sqrt{1}=1\]
c) \[-2a=-4\Rightarrow a=2\]
\[-2b=6\Rightarrow b=-3\]
\[\Rightarrow I\left( 2;-3 \right)\]
\[{{R}^{2}}={{a}^{2}}+{{b}^{2}}-c={{2}^{2}}+{{\left( -3 \right)}^{2}}-\left( -3 \right)=16\Rightarrow R=\sqrt{16}=4\]
Bài 2 (trang 83 SGK Hình học 10): Lập phương trình đường tròn (C) trong các trường hợp sau:
a, (C) có tâm I(-2; 3) và đi qua M(2; -3);
b, (C) có tâm I(-1; 2) và tiếp cúc với đường thẳng x – 2y +7 =0
c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).
Lời giải
a) Ta tìm bán kính \[{{R}^{2}}=I{{M}^{2}}\]\[\Rightarrow {{R}^{2}}=IM={{\left( 2+2 \right)}^{2}}+(-3-{{3}^{2}})=52\]
Phương trình đường tròn (C):
\[{{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=52\]
b) Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
\[d(I;d)=R\]
Ta có : \[R=d(I,d)=\frac{|-1-2.2+7|}{\sqrt{{{1}^{2}}+{{(-2)}^{2}}}}=\frac{2}{\sqrt{5}}\]
Phương trình đường tròn cần tìm là:
\[{{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( \frac{2}{\sqrt{5}} \right)}^{2}}\]
\[\Leftrightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=\frac{4}{5}\]
c) Tâm I là trung điểm của AB, có tọa độ :
\[x=\frac{1+7}{2}=4\], \[y=\frac{1+5}{2}=3\]suy ra I(4;3)
\[AB=2\sqrt{13}\] suy ra \[R=\sqrt{13}\]
Phương trình đường tròn cần tìm là:
\[{{\left( x-4 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=13\]
Bài 3 (trang 84 SGK Hình học 10): Lập phương trình đường tròn đi qua ba điểm:
a, A(1; 2), B(5; 2), C(1; -3)
b, M(-2; 4), N(5; 5), P(6; -2)
Lời giải
Sử dụng phương trình đường tròn có dạng:
\[{{x}^{2}}+{{y}^{2}}-2ax2by+c=0\]
a) Đường tròn đi qua điểm A(1;2) nên ta có:
\[{{1}^{2}}+{{2}^{2}}2a-4b+c=0\Leftrightarrow 2a+4bc=5\]
Đường tròn đi qua điểm B(5;2)nên ta có:
\[52+2210a-4b+c=0\Leftrightarrow 10a+4bc=29\]
Đường tròn đi qua điểm C(1;−3) nên ta có:
\[{{1}^{2}}+{{(-3)}^{2}}2a+6b+c=0\Leftrightarrow 2a-6bc=10\]
Để tìm a,b,c ta giải hệ: 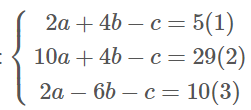
Giải hệ ta được: 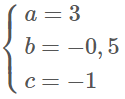
Phương trình đường tròn cần tìm là: \[{{x}^{2}}+{{y}^{2}}-6x+y-1=0\]
b) Tương tự câu a ta được phương trình đường tròn là
\[{{x}^{2}}+{{y}^{2}}-4x2y-20=0\]
Bài 4 (trang 84 SGK Hình học 10): Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và qua điểm M(2; 1).
Lời giải
Gọi \[{{x}_{I}}={{y}_{I}}=a\] .Như vậy phương trình đường tròn cần tìm là :
\[{{\left( 2-a \right)}^{2}}+{{\left( 1-a \right)}^{2}}={{a}^{2}}\]
M(2;1) thuộc đường tròn nên ta có: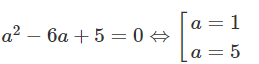
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+) Với a=1\[\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1({{C}_{1}})\]
+) Với a=5 \[\Rightarrow {{\left( x-5 \right)}^{2}}+{{\left( y-5 \right)}^{2}}=25({{C}_{2}})\]
Bài 5 (trang 84 SGK Hình học 10): Lập phương trình của đường tròn tiếp xúc với các trục tọa độ và có tâm nằm trên đường thẳng 4x – 2y – 8 = 0
Lời giải
Gọi (C) là đường tròn cần tìm với tâm I(a;b), bán kính R.
Vì (C) tiếp xúc với hai trục tọa độ nên tâm I của nó phải cách đều hai trục tọa độ.
\[\Rightarrow R=d(I;Ox)=d(I;Oy)\Leftrightarrow \frac{|b|}{\sqrt{1}}=\frac{|a|}{\sqrt{1}}\Leftrightarrow |a|=|b|\]
=> a=b hoặc a=−b
Trường hợp a=b => Tọa độ I(a;a)
Vì I(a;a) nằm trên đường thẳng d:4x–2y–8=0 nên thay tọa độ I vào d ta có:
4.a−2.a−8=0⇔2a=8⇔a=4
=> I(4;4) và bán kính R=4
=> phương trình đường tròn cần tìm: \[{{(x-4)}^{2}}+{{(y-4)}^{2}}=16\ ({{C}_{1}})\]
Trường hợp a=−b => Tọa độ I(a;−a)
Vì I(a;−a) nằm trên đường thẳng d:4x–2y–8=0 nên thay tọa độ I vào d ta có:
\[4.a+2.a-8=0\Leftrightarrow 6a=8\Leftrightarrow a=\frac{4}{3}\]
Suy ra \[I(\frac{4}{3};\frac{-4}{3})\] và bán kính \[R=\frac{4}{3}\]
=> phương trình đường tròn cần tìm: \[{{(x-\frac{4}{3})}^{2}}+{{(y+\frac{4}{3})}^{2}}=\frac{16}{9}\ ({{C}_{2}})\]
Bài 6 (trang 84 SGK Hình học 10): Cho đường tròn C có phương trình: x2 + y2 – 4x + 8y – 5 = 0
a, Tìm tọa độ tâm và bán kính của (C)
b) Viết phương trình tiếp tuyến với (C) đi qua điểm A(−1;0)
c) Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng 3x–4y+5=0
Hướng dẫn gải
a) \[{{x}^{2}}+{{y}^{2}}-4x+8y-5=0\]
\[\Leftrightarrow {{x}^{2}}-2.x.2+{{2}^{2}}+{{y}^{2}}+2.y.4+{{4}^{2}}=25\]
\[\Leftrightarrow {{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{5}^{2}}\]
Tâm I(2;−4), bán kính R=5
b) Phương trình (C) là: \[{{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}={{5}^{2}}\]
Thay tọa độ A(−1;0) vào vế trái, ta có :
\[{{(-1-2)}^{2}}+{{(0+4)}^{2}}={{3}^{2}}+{{4}^{2}}=25\]
Vậy A(−1;0) là điểm thuộc đường tròn (C).
=> Tiếp tuyến với (C) đi qua A chính là tiếp tuyến với (C) tại A.
Ta có: \[\overrightarrow{IA}(-3;4)\]
Phương trình tiếp tuyến với đường tròn tại A là:
\[-3(x+1)+4(y-0)=0\Leftrightarrow 3x-4y+3=0\]
c)
Đường thẳng d:3x–4y+5=0 có véc tơ pháp tuyến \[\vec{n}=(3;-4)\]=> d có vecto chỉ phương là \[\vec{u}=(4;3)\]
Theo giả thiết tiếp tuyến vuông góc với đường thẳng d nên tiếp tuyến có véc tơ pháp tuyến chính là vecto chỉ phương của d
=> vecto pháp tuyến của tiếp tuyến là \[\vec{{n}'}=(4;3)\]
Phương trình tiếp tuyến có dạng là: 4x+3y+c=0.
Khoảng cách từ tâm I đến tiếp tuyến bằng bán kính R=5 do đó ta có:
\[\frac{|4.2+3.(-4)+c|}{\sqrt{{{4}^{2}}+{{3}^{2}}}}=5\Leftrightarrow |c-4|=25\]
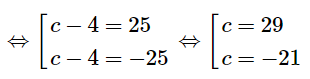
Vậy có hai phương trình tiếp tuyến thỏa mãn yêu cầu bài toán là:
4x+3y+29=0 và 4x+3y−21=0.