Bài 1 ( Trang 68 – SGK)
Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau:
a) 3 giờ;
b) 5 giờ;
c) 6 giờ;
d) 12 giờ;
e) 20 giờ.
Hướng dẫn giải:
Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là: \[{{360}^{0}}:12={{30}^{0}}\]
a) Vào thời điểm 3 giờ thì góc tạo thành giữa hai kim đồng hồ là: \[{{3.30}^{0}}={{90}^{0}}\]
b) Vào thời điểm 5 giờ thì góc tạo thành giữa hai kim đồng hồ là: \[{{5.30}^{0}}={{150}^{0}}\]
c) Vào thời điểm 6 giờ thì góc tạo thành giữa hai kim đồng hồ là: \[{{6.30}^{0}}={{180}^{0}}\]
d) Vào thời điểm 20 giờ thì góc tạo thành giữa hai kim đồng hồ là: \[{{4.30}^{0}}={{120}^{0}}\]
e) Vào thời điểm 12 giờ hai kim đồng hồ trùng nhau thì góc tạo thành giữa hai kim đồng hồ là: \[{{0}^{0}}\].
Bài 2 ( Trang 69 – SGK)
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc \[{{40}^{{}^\circ }}\]. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Giải
Ta có \[\widehat{xOs}={{40}^{{}^\circ }}\] (theo giải thiết)
\[\widehat{tOy}={{40}^{{}^\circ }}\] ( đối đỉnh với \[\widehat{xOs}\])
\[\widehat{xOt}+\text{ }\widehat{tOy}={{180}^{{}^\circ }}\] \[\Rightarrow \widehat{xOt}=-\widehat{tOy}={{180}^{{}^\circ }}-{{40}^{{}^\circ }}={{140}^{{}^\circ }}\]
\[\widehat{yOs}={{140}^{{}^\circ }}\] (đối đỉnh với \[\widehat{xOt}\])
\[\widehat{xOy}=\widehat{sOt}={{180}^{{}^\circ }}\].
Bài 3 ( Trang 69 – SGk)
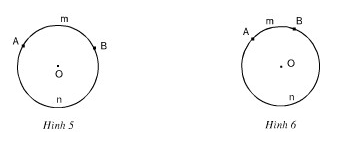
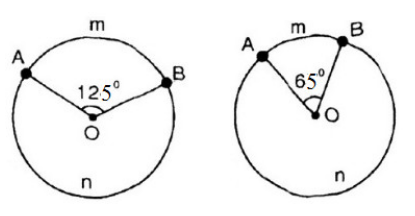
Trên các hình 5, 6, hãy dùng dụng cụ đo góc để tìm số đo cung \[\overset\frown{AmB}\]. Từ đó tính số đo cung \[\overset\frown{AmB}\] tương ứng.
Hướng dẫn giải:
Nối OA, OB.
Đo góc ở tâm \[\widehat{AOB}\] để suy ra số đo cung\[\overset\frown{AmB}\]
Suy ra \[sd\overset\frown{AnB}={{360}^{\circ }}-sd\overset\frown{AmB}\]
a) Hình a. Ta có: \[\widehat{AOB}={{125}^{0}}\] \[\Rightarrow sd\overset\frown{AmB}={{125}^{0}}\]
và \[sd\overset\frown{AnB}=={{360}^{0}}-{{125}^{0}}={{235}^{0}}\]
b) Hình b. Ta có góc \[\widehat{AOB}={{65}^{0}}\]
Suy ra \[sd\overset\frown{AmB}={{65}^{0}}\]
\[sd\overset\frown{AnB}={{360}^{0}}-sd\overset\frown{AmB}={{360}^{0}}-{{65}^{0}}={{295}^{0}}\]
Bài 4 ( Trang 69 – SGk)
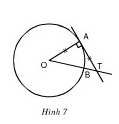
Xem hình 7. Tính số đo góc ở tâm AOB và số đo cung lớn AB.
Hướng dẫn giải:
Ta có OA = AT (gt) nên \(∆AOT\) là tam giác vuông cân tại A, vậy \[\widehat{AOB}={{45}^{0}}\]
Suy ra số đo cung nhỏ \[\overset\frown{AB}={{45}^{0}}.\]
Do đó số đo cung lớn: \[\overset\frown{AB}={{360}^{0}}-{{45}^{0}}={{315}^{0}}\]
Bài 5 ( Trang 69 – SGK)
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết \[\widehat{AMB}\]
a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, OB.
b) Tính số đo mỗi cung AB (cung lớn và cug nhỏ).
Hướng dẫn giải:
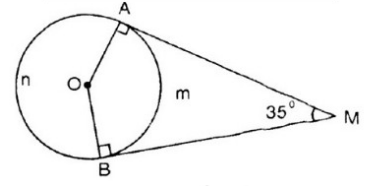
a) Trong tứ giác OBM có: \[\hat{A}=\hat{B}={{90}^{0}}\]
\[\Rightarrow \widehat{AOB}+\widehat{AMB}={{180}^{0}}\]
\[\widehat{AOB}={{180}^{0}}-{{35}^{0}}={{145}^{0}}\]
b) Từ \[\widehat{AOB}={{145}^{0}}\].Suy ra số đo cung nhỏ \[\overset\frown{AB}\] là \[{{145}^{0}}\] và số do cung lớn\[\overset\frown{AB}:{{360}^{0}}-{{145}^{0}}={{215}^{0}}\]
Bài 6 ( Trang 69 – SGK)
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua ba đỉnh A, B, C.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
Hướng dẫn giải:
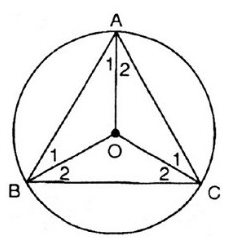
a) Ta có: \[\hat{A}=\hat{B}=\hat{C}={{60}^{0}}\] (gt)
Suy ra \[\widehat{{{A}_{1}}}=\widehat{{{A}_{2}}}=\widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}=\widehat{{{C}_{1}}}=\widehat{{{C}_{2}}}={{30}^{0}}\]
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: \[\widehat{AOB}={{180}^{0}}-\widehat{{{A}_{1}}}-\widehat{{{B}_{1}}}={{180}^{0}}-{{30}^{0}}-{{30}^{0}}={{120}^{0}}\]
Tương tự ta suy ra: \[\widehat{AOB}=\widehat{BOC}=\widehat{COA}={{120}^{0}}\]
b) Từ \[\widehat{AOB}=\widehat{BOC}=\widehat{COA}={{120}^{0}}\] ta suy ra:
\[sdABC=sdBCA=sdCAB={{240}^{0}}\]
Bài 7 ( Trang 69 – SGK)
ho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (h.8)
a)Em có nhận xét gì về số đo của các cung AM, CP, BN, DQ
b) Hãy nêu tên các cung nhỏ bằng nhau.
c) Hãy nêu tên hai cung lớn bằng nhau.
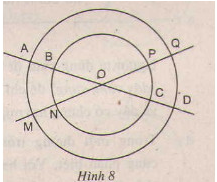
Hướng dẫn giải:
a) Các cung nhỏ \[AM,CP,BN,DQ\] có cùng số đo
b) \[\overset\frown{AM}=\overset\frown{DQ}=\overset\frown{BN}=\overset\frown{PC}\];
\[\overset\frown{AQ}=\overset\frown{MD}=\overset\frown{BP}=\overset\frown{NC}\]
c) Các cung lớn bằng nhau: \[\overset\frown{AMDQ}=\overset\frown{MAQD};\] \[\overset\frown{BNCP}=\overset\frown{NBPC}\]
Bài 8 ( Trang 70 – SGK)
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì có số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
Hướng dẫn giải:
a) Đúng
b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
c) Sai( như trên)
d) Đúng
Bài 9 ( Trang 70- SGK)
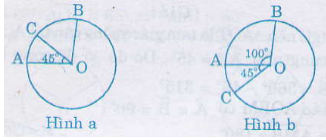
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho \[\widehat{AOB}={{100}^{0}}\]; \[sdAC={{45}^{0}}\]. Tính số đo của cung nhỏ BC và cung lớn BC. Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cung lớn AB.
Hướng dẫn giải
a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ \[\overset\frown{BC}={{100}^{0}}-{{45}^{0}}={{55}^{0}}\]
Số đo cung lớn \[\overset\frown{BC}={{360}^{0}}-{{55}^{0}}={{305}^{0}}\]
b) Điểm C nằm trên cung lớn ( hình b)
Số đo cung nhỏ \[\overset\frown{BC}={{100}^{0}}+{{45}^{0}}={{145}^{0}}\]
Số đo cung lớn \[\overset\frown{BC}={{360}^{0}}-{{145}^{0}}={{215}^{0}}\]