Bài 33 ( Trang 93 – SGK)
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 41, sinα bằng
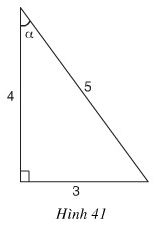
(A) \[\frac{5}{3}\] (B) \[\frac{5}{4}\] (C) \[\frac{3}{5}\] (D) \[\frac{3}{4}\]
b) Trong hình 42, sin Q bằng
.png)
(A) \[\frac{P\text{R}}{R\text{S}}\] (B) \[\frac{P\text{R}}{QR}\] (C) \[\frac{P\text{S}}{S\text{R}}\] (D) \[\frac{S\text{R}}{Q\text{R}}\]
c) Trong hình 43, cos 30° bằng
.png)
(A) \[\frac{2\text{a}}{\sqrt{3}}\] (B) \[\frac{a}{\sqrt{3}}\] (C) \[\frac{\sqrt{3}}{2}\] (D) \[2\sqrt{3}{{a}^{2}}\]
Hướng dẫn làm bài:
a) Chọn (C)
b) Chọn (D)
c) Chọn (C) vì: \[\cos {{30}^{0}}=\frac{\sqrt{3}a}{2a}=\frac{a\sqrt{3}}{2a}\]
Bài 34 ( Trang 93 – SGK)
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
.png)
(A) \[\sin \alpha =\frac{b}{c}\] (B) \[\text{cotg}\alpha =\frac{b}{c}\]
(C) \[tg\alpha =\frac{a}{c}\] (D) \[\text{cotg}\alpha =\frac{a}{c}\]
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng?
.png)
(A) sin2α + cos2 α = 1;
(B) sin α = cos β;
(C) cos β = sin(90°- α);
(D) \[tg\alpha =\frac{\sin \alpha }{\cos \alpha }\]
Hướng dẫn làm bài:
a) Chọn C
b) Chọn C vì: cosβ = sin(90°-α) ⇔ α = β = 45°
Bài 35 ( Trang 94 – SGK)
Tỉ số giữa hai cạnh góc vuông của một hình tam giác vuông bằng 19 : 28. Tìm các góc của nó.
Hướng dẫn làm bài:
.png)
Gọi α là góc nhọn của tam giác vuông đó có:
\[tg\alpha =\frac{19}{28}\approx 0,6786\Rightarrow \alpha \approx {{34}^{0}}1{0}'\]
Vậy các góc nhọn của tam giác vuông đó có độ lớn là:
α ≈ 34°10’; β ≈ 90° - 34°10’ = 55°50’
Bài 36 ( Trang 94 - SGK)
Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47)
Hướng dẫn làm bài:
.png)
Xét hình 46, ta có:
BH < HC ⇒ AB < AC
∆HAB vuông tại H có góc ABH = 45° nên là tam giác vuông cân ⇒ AH = BH = 20 (cm)
∆HAC vuông tại H, theo định lí Py-ta-go có:
AC2 = AH2 + HC2 = 212 + 202
\[\Rightarrow AC=\sqrt{{{21}^{2}}+{{20}^{2}}}=29(cm)\]
Xét hình 47, ta có:
BH > HC ⇒ AB > AC
∆ABH vuông tại H có góc B = 45° nên là tam giác vuông cân ⇒ AH = BH = 21 (cm)
\[\Rightarrow AB=\sqrt{{{21}^{2}}+{{21}^{2}}}=21\sqrt{2}\approx 29,7(cm)\]
Bài 37 ( Trang 94 – sGK)
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nắm trên đường nào?
Hướng dẫn làm bài:
.png)
a) Ta có: 62 + 4,52 = 36 + 20,25 = 56,25 = 7,52 = 56,25
∆ABC có AB2 + AC2 = BC2 (=56,25) nên vuông tại A.
\[tgB=\frac{AC}{AB}=\frac{4,5}{6}=0,75\Rightarrow \hat{B}\approx {{37}^{0}}\]
\[\hat{C}={{90}^{0}}-\hat{B}\approx {{53}^{0}}\]
∆ABC vuông tại A, AH là đường cao nên:
AH.BC = AB.AC
\[\Rightarrow AH=\frac{AB.AC}{BC}=\frac{4,5.6}{7,5}=3,6(cm)\]
b) SMBC = SABC ⇒ M cách BC một khoảng bằng AH.
Do đó M nằm trên hai đường thẳng song song cách BC một khoảng bằng 3,6 cm
Bài 38 ( Trang 94 – SGK)
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)
.png)
Hướng dẫn làm bài:
.png)
\[\widehat{IKB}={{50}^{0}}+{{15}^{0}}={{65}^{0}}\]
∆IBK vuông tại I nên IB = IK. tgIKB = 380 . tg65° ≈ 814,9 (cm)
∆IAK vuông tại I nên IA = IK. tgIKA = 380 . tg50° ≈ 452,9 (cm)
Khoảng cách giữa hai thuyền là: AB = IB – IA ≈ 362 (m)
Bài 39 ( Trang 95 – SGK)
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
.png)
Hướng dẫn làm bài:
Khoảng cách giữa hai cọc là:
\[\frac{20}{\cos {{50}^{0}}}-\frac{5}{\sin {{50}^{0}}}\approx 31,12-6,53\approx 24,59(m)\]
Bài 40 ( Trang 95 – SGK)
Tính chiều cao của cây trong hình 50 (làm tròn đến đề - xi – mét)
.png)
Hướng dẫn làm bài:
.png)
Chiều cao của cây là:
1,7 + 30tg35° ≈ 1,7 + 21 = 22,7 (cm)
Bài 41 ( Trang 96 – SGK)
Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, \[\widehat{BAC}=x,\widehat{ABC}=y\] Dùng các thông tin sau (nếu cần) để tìm x – y:
sin 23°36’ ≈ 0,4;
cos66°24’ ≈ 0,4;
tg21°48’ ≈ 0,4
.png)
\[tgy=\frac{2}{5}=0,4\] nên y ≈ 21°48’
Do đó: x = 90° - y ≈ 68°12’
Vậy: x – y ≈ 68°12’ - 21°48’ ≈ 46°24’
Bài 42 ( Trang 96 – SGK)
Ở một cái thang dài 3m người ta ghi: “ Để đảm bảo an toàn khi dùng thang phải đặt thang này tạo với mặt đất một góc có độ lớn từ \[{{60}^{0}}\]đến \[{{70}^{0}}\] “.Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường bao nhiêu mét để đảm bảo an toàn.
Giải
.png)
\[AC=AB\cos C=3\cos {{60}^{0}}=1,5(m)\]
\[{A}'{C}'={A}'{B}'\cos {C}'=3\cos {{70}^{0}}\approx 1,03(m)\]
Vậy khi dùng thang đó, chân thang phải đặt cách tường một khoảng từ 1,03m đến 1,5m để đảm bảo an toàn.
Bài 43 ( Trang 96 – SGk)
Đố
.png)
Vào khoảng năm 200 trước Công nguyên, Ơ-ra—tô-xten, một nhà Toán học và thiên văn học Hi Lạp, đã ước lượng được “chu vi” của Trái Đất (chi vi đường Xích Đạo) nhờ hai quan sát sau:
1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (Nay gọi là Át –xu-an), tức là tia sáng chiếu thẳng đứng.
2) Cùng lúc đó ở thành phố A-lếch-săng-đri-a cách Xy-en 800km, một tháp cao 25cm có bóng trên mặt đất dài 3,1m
Từ hai quan sát trên, em hãy tính xấp xỉ “chu vi” Trái Đất.
(Trên hình 5, điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trung cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB)
Hướng dẫn làm bài:
.png)
Bóng của tháp vuông góc với tháp:
∆ABC vuông tại A. Ta có:
\[tgC=\frac{AB}{AC}=\frac{3,1}{25}\approx 0,124\Rightarrow \hat{C}={{7}^{0}}\]
Các tia sáng được coi là song song với nhau nên \[\hat{O}={{7}^{0}}\]
Chu vi của Trái Đất là: \[800.\frac{360}{7}\approx 41143(km)\]
