Bài 20 ( Trang 19 – SGK)
Giải các hệ phương trình sau bằng phương pháp cộng đại số.
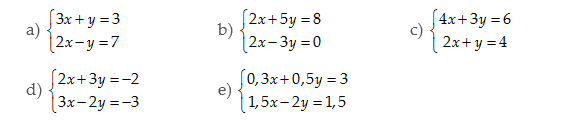
Bài giải:
.png)
Bài 21 ( Trang 19 – SGK)
Giải các hệ phương trình sau bằng phương pháp cộng đại số.
.png)
Bài giải:
.png)
b) Nhân phương trình thứ nhất với \[\sqrt{2}\] rồi cộng từng vế hai phương trình ta được:
\[5x\sqrt{6}+x\sqrt{6}=6\Leftrightarrow x=\frac{1}{\sqrt{6}}\]. Từ đó hệ đã cho tương đương với
.png)
Bài 22 ( Trang 19 – SGK)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
.png)
Bài giải:
.png)
Hệ phương trình có vô số nghiệm.
Bài 23 ( Trang 19 - SGK)
Giải hệ phương trình sau:
.png)
Bài giải:
Ta có:
.png)
Trừ từng vế hai phương trình (1) và (2) ta được:
\[(1-\sqrt{2})y-(1+\sqrt{2})y=2\Leftrightarrow (1-\sqrt{2}-1-\sqrt{2})y=2\]
\[\Leftrightarrow -2y\sqrt{2}=2\Leftrightarrow y=\frac{-2}{2\sqrt{2}}\]
\[\Leftrightarrow y=\frac{-1}{\sqrt{2}}\Leftrightarrow y=\frac{-\sqrt{2}}{2}\]
Thay (3) vào (1) ta được:
\[\Leftrightarrow (1+\sqrt{2})x+(1-\sqrt{2})(\frac{-\sqrt{2}}{2})=5\Leftrightarrow (1+\sqrt{2})x+(\frac{-\sqrt{2}}{2})+1=5\]
\[\Leftrightarrow (1+\sqrt{2})x=\frac{8+\sqrt{2}}{2}\Leftrightarrow x=\frac{8+\sqrt{2}}{2(1+\sqrt{2})}\]
\[\Leftrightarrow x=\frac{(8+\sqrt{2})(1-\sqrt{2})}{2(1-2)}\Leftrightarrow x=\frac{8-8\sqrt{2}+\sqrt{2}-2}{-2}\]
\[\Leftrightarrow x=-\frac{6-7\sqrt{2}}{2}\Leftrightarrow x=\frac{-6+7\sqrt{2}}{2}\]
.png)
Bài 24 ( Trang 19 – SGK)
Giải hệ các phương trình:
.png)
Bài giải:
a) Đặt x + y = u, x - y = v, ta có hệ phương trình (ẩn u, v):
.png)
.png)
Bài 25 ( Trang 19 – SGK)
Ta biết rằng: Một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0. Hãy tìm các giá trị của m và n để đa thức sau (với biến số x) bằng đa thức 0:
P(x) = (3m - 5n + 1)x + (4m - n -10).
Bài giải:
Ta có P(x) = (3m - 5n + 1)x + (4m - n -10)
.png)
Bài 26 ( Trang 19 – SGK)
Xác định a và b để đồ thị của hàm số y = ax + b đi qua điểm A và B trong mỗi trường hợp sau:
a) A(2; -2) và B(-1; 3); b) A(-4; -2) và B(2; 1);
c) A(3; -1) và B(-3; 2); d) \[A(\sqrt{3};2)\] và B(0; 2).
Bài giải:
a) Vì \(A(2; -2)\) thuộc đồ thì nên \(2a + b = -2\).
Vì \(B(-1; 3)\) thuộc đồ thì nên \(-a + b = 3\). Ta có hệ phương trình ẩn là a và b.
.png)
b) Vì A(-4; -2) thuộc đồ thị nên -4a + b = -2
Vì B(2; 1) thuộc đồ thị nên 2a + b = 1.
Ta có hệ phương trình ẩn là a, b:
.png)
c) Vì A(3; -1) thuộc đồ thị nên 3a + b = -1
Vì B(-3; 2) thuộc đồ thị nên -3a + b = 2.
Ta có hệ phương trình ẩn a, b:
.png)
d) Vì \(A(\sqrt{3}; 2)\) thuộc đồ thị nên \(\sqrt{3}a + b = 2\).
Vì \(B(0; 2)\) thuộc đồ thị nên \(0 . a + b = 2\).
Ta có hệ phương trình ẩn là a, b.
.png)
Bài 27 ( Trang 20 – SGK)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhật hai ẩn rồi giải:
.png)
Bài giải:
a) Điền kiện x ≠ 0, y ≠ 0.
.png)
\[(1)\Leftrightarrow u=1+v\] (3)
Thế (3) vào (2): 3(1 + v) +4v = 5
\[3(1+v)+4v=5\Leftrightarrow 3+3v+4v=5\Leftrightarrow 7v=2\Leftrightarrow v=\frac{2}{7}\]
Từ đó \[u=1+v=1+\frac{2}{7}=\frac{9}{7}\]
.png)
b) Điều kiện x - 2 ≠ 0, y - 1 ≠ 0 hay x ≠ 2, y ≠ 1.
Đặt \[u=\frac{1}{x-2},\text{ }v=\frac{1}{y-1}\] ta được hệ đã cho tương đương với:
.png)
(1) ⇔ v = 2 – u (3)
Thế (3) vào (2): 2u - 3(2 - u) = 1
\[\Leftrightarrow 2u-6+3u=1\Leftrightarrow 5u=7\Leftrightarrow u=\frac{7}{5}\]
Từ đó \[v=2-\frac{7}{5}=\frac{3}{5}\]
Suy ra hệ đã cho tương đương với:
.png)
