Bài 65 ( Trang 95 SGK)
Lấy giá trị gần đúng của π là 3,14, hãy điền vào ô trống trong bảng sau (đơn vị độ dài:cm, làm tròn kết quả đến chữ thập phân thứ hai).

Giải
Từ \[C=2pR\Rightarrow R=\frac{C}{2\pi };\] \[C=pd\Rightarrow d=\frac{C}{\pi }\]
Vậy dùng các công thức trên để tìm các giá trị chưa biết trong ô trống. Ta điền vào bảng sau:

Bài 66 ( Trang 95 – SGK)
a) Tính độ dài cung \[{{60}^{0}}\] của mộ đường tròn có bán kính 2 dm.
b) Tính chu vi vành xe đạp có đường kính 650mm.
Hướng dẫn giải:
a) Áp dụng số vào công thức \[l=\frac{\pi Rn}{180}\], ta có:
\[l=\frac{3,14.2.60}{180}=2,09(dm)\approx 21(cm)\]
b) Độ dài vành xe đạp là: 3,14. 650 = 2041 (mm) ≈ 2(m)
Bài 67 ( Trang 95 – SGK)
Lấy giá trị gần đúng của π là 3,14, hãy điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất và đến độ):

Hướng dẫn giải:
Vận dụng công thức: \[l=\frac{\pi Rn}{180}\] để tìm R hoặc \[{{n}^{0}}\] hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:

Bài 68 ( Trang 95 – SGK)
Cho ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Hướng dẫn giải:
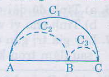
Gọi \[{{C}_{1}};{{C}_{2}};{{C}_{3}}\] lần lượt là độ dài của các nửa đường tròn đường kính AC, AB, BC, ta có:
\[{{C}_{1}}\]= π. AC (1)
\[{{C}_{2}}\]= π.AB (2)
\[{{C}_{3}}\]= π.BC (3)
So sánh (1), (2), (3) ta thấy: \[{{C}_{2}}+{{C}_{3}}=\pi \left( AB+BC \right)=\pi AC\]
Vậy \[{{C}_{1}}={{C}_{2}}+{{C}_{3}}\].
Bài 69 ( Trang 95 – SGK)
Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có đường kính 1,672 m và bánh xe trước có đường kính là 88cm. Hỏi khi bánh xe sau lăn được 10 vòng thì bánh xe trước lăn được mấy vòng?

Hướng dẫn giải:
Chu vi bánh xe sau: π. 1,672 (m)
Chu vi bánh xe trước: π . 0,88 (m)
Khi bánh xe sau lăn được 10 vòng thì quãng đường đi được là: π . 16,72 (m)
Khi đó số vòng lăn của bánh xe trước là: \[\frac{\pi .16,72}{\pi .0,88}=19\] (vòng)
Bài 70 ( Trang 95 – SGK)
Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo) 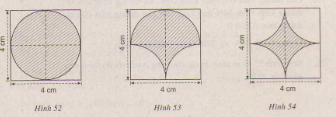
Hướng dẫn giải:
Cách vẽ:
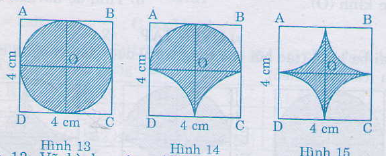
- Hình 13: Vẽ hình vuông ABCD cạnh 4 cm. Vẽ hai đường trung trực của các cạnh hình vuông, chúng cắt nhau tại O.
Lấy O làm tâm vẽ đường tròn bán kính 2cm ta được hình a.
- Hình 14: Vẽ hình vuông như hình a. Lấy O làm tâm vẽ nửa đường tròn bán kính 2 cm tiếp xúc với các cạnh AB, AD, BC. Lấy C, D làm tâm vẽ cung phần tư đường tròn về phía trong hình vuông các cung tròn đã vẽ tạo nên hình b .
- Hình 15: Vẽ hình vuông như hình a. Lấy A,B,C,D làm tâm vẽ về phía trong hình vuông bốn cung tròn, mỗi cung là phần tư đường tròn. Bốn cung này tạo nên hình c.
Tính chu vi mỗi hình:
- Hình 13: Đường kính đường tròn này là 4 cm.
Vậy hình tròn có chu vi là: 3,14 . 4 = 12,56 (cm).
- Hình 14: Hình tròn gồnm hai cung: một cung là nửa đường tròn, hai cung có mỗi cung là phần tư đường tròn nên chu vi hình bằng chu vi của hình tròn ở hình a, tức là 12,56 (cm).
- Hình 15: Hình gồm bốn cung tròn với mỗi cung tròn là phần tư đường tròn nên chu vi hình bằng chu vi hình tròn ở hình a tức là 12,56 cm.
Bài 71 ( Trang 96 – SGk)
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (hình vuông ABCD dài 1cm ). Nếu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
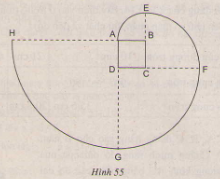
Hướng dẫn giải:
Cách vẽ: Vẽ hình vuông ABCD có cạnh dài 1cm.
Vẽ \[\frac{1}{4}\] đường tròn tâm B, bán kính 1 cm, ta có cung AE
Vẽ \[\frac{1}{4}\] đường tròn tâm C, bán kính 2 cm, ta có cung EF
Vẽ \[\frac{1}{4}\] đường tròn tâm D, bán kính 3 cm, ta có cung FG
Vẽ \[\frac{1}{4}\] đường tròn tâm A, bán kính 4 cm, ta có cung GH
Độ dài đường xoắn: \[\overset\frown{AE}=\frac{1}{4}.2p.1\] (1)
\[\overset\frown{EF}=\frac{1}{4}.2p.2\] (2)
\[\overset\frown{FG}=\frac{1}{4}.2p.3\] (3)
\[\overset\frown{GH}=\frac{1}{4}.2p.4\](4)
Vậy: Độ dài đường xoắn là: (1) + (2) + (3) +(4) = \[5\pi \]
Bài 72 ( Trang 96 – SGK)
Bánh xe của một ròng rọc có chu vi là 540mm. Dây cua-roa bao bánh xe theo cung AB có độ dài 200mm. Tính góc AOB (h.56)
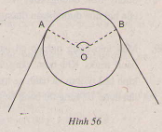
\[{{360}^{0}}\] ứng với 540mm
\[{{x}^{0}}\] ứng với 200mm
\[x=\frac{360.200}{540}\approx {{133}^{0}}\]
Vậy \[sd\overset\frown{AB}\approx {{133}^{0}}\] suy ra \[\widehat{AOB}\approx {{133}^{0}}\]
Bài 73 ( Trang 96 – SGK)
Đường tròn lớn của Trái Đất dài khoảng 40000km. Tính bán kính Trái Đất.
Hướng dẫn giải:
Gọi bán kính Trái Đất là R thì độ dài kinh tuyến Trái Đất là πR (giả thiết Trái Đất tròn và kinh tuyến bằng nửa đường tròn lớn).
Do đó: πR = 20000km \[\Rightarrow R=\frac{20000}{\pi }=\frac{20000}{3,14}\approx 6369(km)\]
Bài 74 ( Trang 96 – SGK)
Vĩ độ của Hà Nội là \[{{20}^{0}}0{1}'\].Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Tính độ dài cung kinh tuyến từ Hà Nội đến xích đạo.
Hướng dẫn giải:
Vĩ độ của Hà Nội là 20^001’ có nghĩa là cung kinh tuyến từ Hà Nội đến xích đạo có số đo là \[{{(20\tfrac{1}{60})}^{{}^\circ }}\]. Vậy độ dài cung kinh tuyến từ Hà Nội đến xích đạo là:
\[l=\frac{40000.20\frac{1}{60}}{360}\approx 2224(km)\]
Bài 75 ( Trang 96 – SGK)
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm (O'), đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh cung MA và cung MB có cùng độ dài bằng nhau.
Hướng dẫn giải:
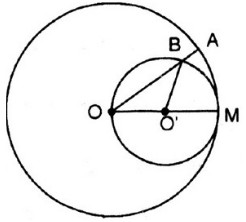
Đặt \[\widehat{MOB}=\alpha \text{ }\] \[\Rightarrow \widehat{M{O}'B}=2\alpha \] (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là: \[\overset\frown{MB}=\frac{\pi .{O}'M.2\alpha }{{{180}^{0}}}=\frac{\pi .{O}'M.\alpha }{{{90}^{0}}}(1)\]
Độ dài cung MA là: \[\overset\frown{MA}=\frac{\pi .OM.\alpha }{{{180}^{0}}}=\frac{2\pi .{O}'M.\alpha }{{{180}^{0}}}=\frac{\pi {O}'M.\alpha }{{{90}^{0}}}(2)\]
Vì OM = 2O’M
Từ (1) và (2) \[\Rightarrow \overset\frown{MB}=\overset\frown{MA}\].
Bài 76 ( Trang 96 – SGK)
Xem hình 57 và so sánh độ dài của cung AmB với độ dài đường gấp khúc AOB.
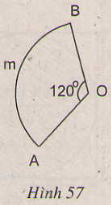
Hướng dẫn giải:
Ta có: \[\overset\frown{AmB}=\frac{2\pi R}{3}=2R\frac{\pi }{3}\]
Độ dài đường gấp khúc AOB là d: => d = AO + OB = R + R = 2R
Mà π > 3 nên \[\frac{\pi }{3}>1\] , do đó: \[\overset\frown{AmB}\] > d.
