Bài 10 ( Trang 104 – SGK)
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC
Giải
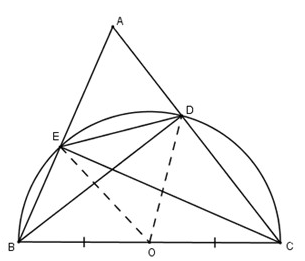
a) Gọi O là trung điểm của BC.
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
\[EO=\frac{1}{2}BC;DO=\frac{1}{2}BC\]
Suy ra \[OE=OD=OB=OC(=\frac{1}{2}BC)\]
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường \[\left( O;\frac{BC}{2} \right)\], BC là đường kính, DE là một dây cung không đi qua tâm, do đó DE < BC.
Bài 11 ( Trang 104 – SGK)
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý:
Kẻ OM vuông góc với CD.
Giải
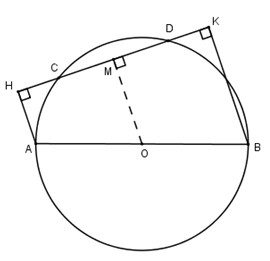
Vẽ \[OM\bot CD\]
Xét tam giác OCD có:
.png)
Tam giác OCD cân tại O có OM là đường cao nên cũng đồng thời là đường trung tuyến.
\[\Rightarrow MC=MD\] (1)
Xét hình thang AHKB, ta có:
OM // AH //BK (cùng vuông góc với CD)
\[AO=BO=\frac{AB}{2}\]
Vậy MO là đường trung bình của hình thang AHKB
\[\Rightarrow MH=MK\] (2)
Từ (1) và (2) \[\Rightarrow CH=DK\]
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau
