Bài 35 ( Trang 122 – sGK)
Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O;R) và (O';r) có OO' = d, R > r.
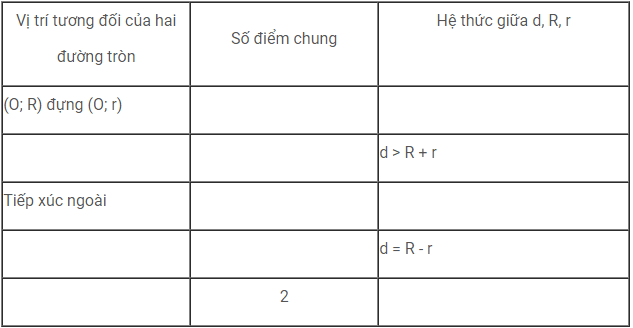
Giải
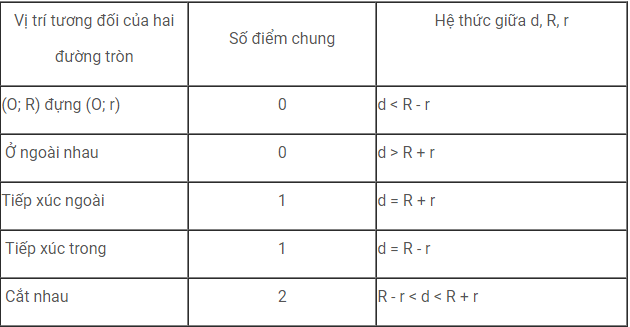
Bài 36 ( Trang 123 – SGK)
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
a) Hãy xác định vị trí tương đối của hai đường tròn.
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.
Giải:
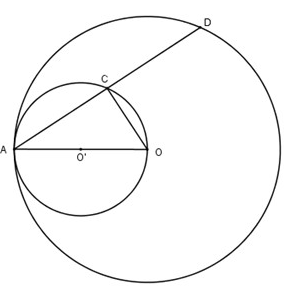
a) Gọi O' là tâm của đường tròn đường kính OA thì O'A = O'O.
Ta có OO' = OA - O'A hay d = R - r
Suy ra đường tròn (O) và đường tròn (O') tiếp xúc trong.
b) Tam giác CAO có cạnh OA là đường kính của đường tròn ngoại tiếp nên \[\Delta CAO\] vuông tại C
\[\Rightarrow OC\bot AD\]
\[\Rightarrow CA=CD\] (đường kính vuông góc với một dây).
Bài 37 ( Trang 123 – SGK)
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.
Giải:
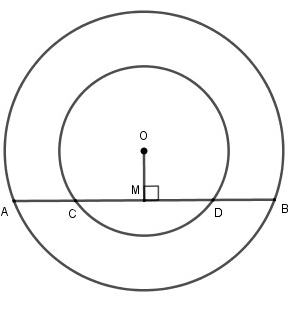
Vẽ \[OM\bot AB\]
Theo tính chất đường kính vuông góc với một dây ta được MA = MB và MC = MD.
Từ đó suy ra AC = BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
Bài 38 ( Trang 123 – SGK)
Điền các từ thích hợp vào chỗ trống (...) :
a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O;3cm) nằm trên ...
b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O;3cm) nằm trên ...
Giải:
a)
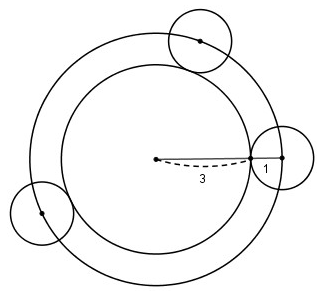
Hai đường tròn tiếp xúc ngoài nên d = R + r = 3 + 1 = 4 (cm).
Trả lời: Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O;3cm) nằm trên đường tròn (O; 4cm).
b)
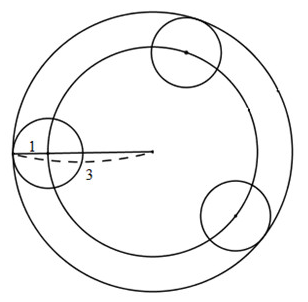
Hai đường tròn tiếp xúc trong nên d = R – r = 3 – 1 = 2 (cm).
Trả lời: Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O;3cm) nằm trên đường tròn (O;2cm).
Bài 39 ( Trang 123 – SGK)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, \[B\in (O)\], \[C\in ({O}')\]. Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh rằng \[\widehat{BAC}={{90}^{{}^\circ }}\]
b) Tính số đo góc OIO'.
c) Tính độ dài BC, biết OA = 9 cm, O'A = 4cm.
Giải:
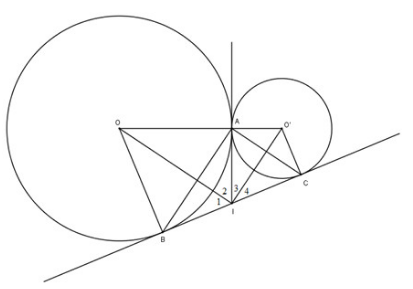
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có \[IA=IB=IC=\frac{1}{2}BC\]
Do đó tam giác ABC vuông tại A
\[\Rightarrow \widehat{BAC}={{90}^{{}^\circ }}\]
b)
Ta có \[{{\hat{I}}_{1}}={{\hat{I}}_{2}};{{\hat{I}}_{3}}={{\hat{I}}_{4}}\] (tính chất hai tiếp tuyến cắt nhau).
Do đó \[\widehat{OI{O}'}={{90}^{{}^\circ }}\] (hai tia phân giác của hai góc kề bù).
c) Ta có \[AI\bot O{O}'\]
Xét tam giác OIO' vuông tại I, ta có:
\[I{{A}^{2}}=OA\cdot {O}'A=9\cdot 4=36\Rightarrow IA=6\]
Do đó BC = 12cm.
Nhận xét. Câu a), b) chỉ là gợi ý để làm câu c). Đối với những bài toán có hai đường tròn tiếp xúc, ta thường vẽ thêm tiếp tuyến chung tại tiếp điểm để xuất hiện yếu tố trung gian giúp cho việc tính toán hoặc chứng minh được thuận lợi.
Bài 40 ( Trang 123 – sGK)
Trên các hình 99a, 99b, 99c, các bánh xe tròn có răng cưa được khớp với nhau. Trên hình nào hệ thống bánh răng chuyển động được? Trên hình nào hệ thống bánh răng không chuyển động được?
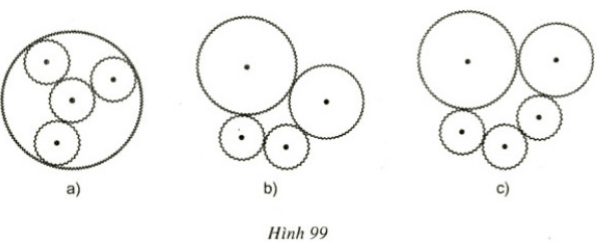
Hướng dẫn giải:
Trong hệ thống các bánh xe răng cưa thì hai bánh xe răng cưa tiếp xúc ngoài bao giờ cũng chuyển động ngược chiều nhau, hai bánh răng cưa tiếp xúc trong bao giờ cũng chuyển động cùng chiều nhau. Vì vậy hệ thống bánh răng ở hình a), hình b) chuyển động được. Hệ thống bánh răng ở hình c) không chuyển động được.
