Bài 17 ( Trang 109 – SGk)
Điền vào các chỗ trống (...) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng) :
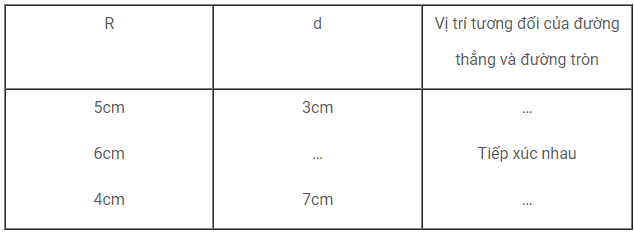
Giải
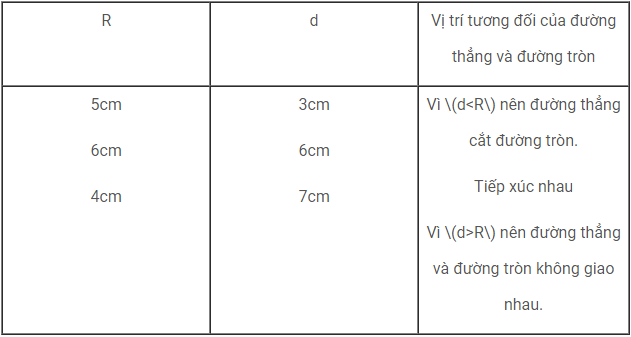
Bài 18 ( Trang 110 – SGK)
Trên mặt phẳng tọa độ Oxy, cho điểm A(3;4). Hãy xác định vị trí tương đối của đường tròn (A;3) và các trục tọa độ.
Giải:
.png)
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d > R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d = R, do đó đường tròn và trục Oy tiếp xúc nhau.
Bài 19 ( Trang 110 – SGK)
Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?
Giải:
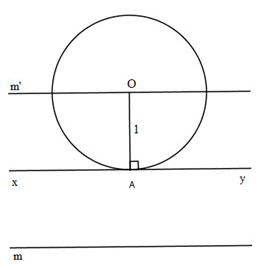
Gọi O là tâm của đường tròn bán kính 1cm và tiếp xúc với đường thẳng xy.
Vì d = R = 1cm nên điểm O cách đường thẳng xy là 1cm, do đó O nằm trên hai đường thẳng m và m' song song với xy và cách xy là 1cm.
Bài 20 ( Trang 110 – SGK)
Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.
Giải:
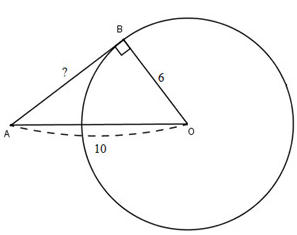
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
\[AB=\sqrt{A{{O}^{2}}-O{{B}^{2}}}=\sqrt{{{10}^{2}}-{{6}^{2}}}=8(cm)\]
