Bài 33 ( Trang 119 – SGK)
Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O'D.
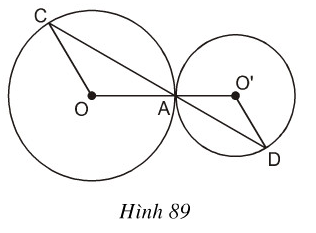
Giải:
(O) và (O’) tiêó xúc nhau tại A (gt) ⇒ O, A, O’ thẳng hàng.
∆OCA có OC = OA (= R) nên tam giác cân tại O
\[\Rightarrow \widehat{OAC}=\widehat{OC\text{A}}\]
Tương tự có \[\widehat{{O}'A\text{D}}=\widehat{{O}'DA}\] mà \[\widehat{OAC}=\widehat{{O}'\text{AD}}\] (đối đỉnh)
Suy ra \[\widehat{OC\text{A}}=\widehat{{O}'DA}\] mà góc \[\widehat{OC\text{A}}\] và \[\widehat{{O}'D\text{A}}\] so le trong, do đó OC // O’D (đpcm)
Bài 34 ( Trang 119 – SGK)
Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
Giải:
Vẽ dây cung AB cắt OO' tại H.
Ta có \[AB\bot O{O}'\] và HA = HB = 12cm.
Ta có:
\[O{{H}^{2}}=O{{A}^{2}}-A{{H}^{2}}={{20}^{2}}-{{12}^{2}}=256\Rightarrow OH=16cm.\]
* Nếu O và O' nằm khác phía đối với AB (h.a)
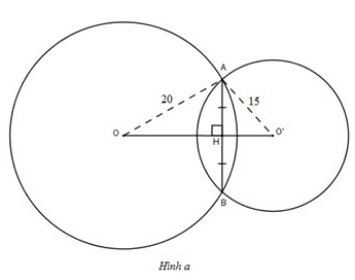
thì OO' = 16 + 9 = 25 (cm).
*Nếu O và O' nằm cùng phía đối với AB (h.b)
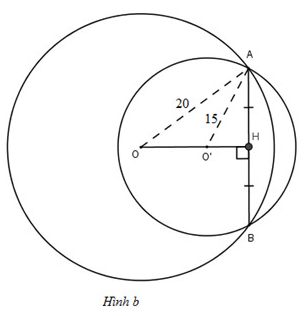
thì OO' = 16 – 9 = 7 (cm).
