A. TÓM TẮT LÝ THUYẾT
1. Tia phân giác của góc
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
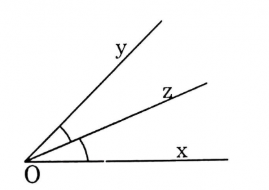
(Trong hình trên, tia Oz là tia phân giác của góc xOy)
Nhận xét: Nếu tia Oz là tia phân giác của góc xOy thì \[\widehat{xOz}=\widehat{yOz}=\frac{\widehat{xOy}}{2}\]
2. Cách vẽ tia phân giác của 1 góc
Cách 1: Dùng thước đo góc
.png)
Cách 2: Gấp giấy
.png)
3. Chú ý
Đường thẳng chứa tia phân giác gọi là đường phân giác của góc đó.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Câu 30: Trang 87 - SGK Toán 6 tập 2
Trên cùng một nửa mặt phẳng chứa bờ Ox, vẽ tia Ot sao cho góc \[\widehat{xOt}\] =250 , \[\widehat{xOy}\]= 500.
a) Tia Ot có nằm giữa hai tia Ox và Oy không?
b) So sánh góc tOy và góc xOt.
c ) Tia Ot có là tia phân giác của góc xOy không? Vì sao?
Lời giải chi tiết
a) Tia Ot nằm giữa hai tia Ox và Oy (1) vì các tia Ot,Oy cùng thuộc nửa mặt phẳng bờ chứa Ox và \[\widehat{xOt}\]<\[\widehat{xOy}\]
b) Tia Ot nằm giữa hai tia Ox,Oy nên:
\[\widehat{xOt}\]+ \[\widehat{yOt}\]=\[\widehat{xOy}\]
do đó
250+ \[\widehat{yOt}\]=500
suy ra \[\widehat{yOt}\]= 500- 250 =250 vậy \[\widehat{xOt}\]=\[\widehat{yOt}\] (2)
c) Từ (1) và (2) ta có:Tia Ot nằm giữa hai tia Ox và Oy và \[\widehat{xOt}\]=\[\widehat{yOt}\] nên suy ra Ot là tia phân giác của góc xOy.
Câu 31: Trang 87 - SGK Toán 6 tập 2
a) Vẽ góc xOy có số đo 1260
b) Vẽ tia phân giác của góc xOy ở câu a.
Lời giải chi tiết
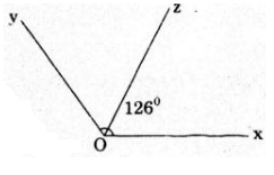
a)Dùng thước đo góc ta vẽ được góc xOy = 126o
Cách vẽ: đặt thước đo góc trên nửa mặt phẳng có bờ chứa tia Ox sao cho tâm của thước trùng với gốc O của tia Ox và tia Ox đi qua vạch O của thước.
Kẻ tia Oy đi qua vạch 126 độ của thước đo góc. Vậy ta được góc xOy thỏa mãn yêu cầu bài toán.
b) Vì tia Oz là tia phân giác của góc xOy
Chú ý rằng \[\widehat{xOz}\]=\[\widehat{zOy}\]=\[\frac{\widehat{xOy}}{2}\]=630
Đặt thước đo góc nằm cùng tia Oy trên nửa mặt phẳng bờ là đường thẳng chứa tia Ox trùng với đỉnh O của góc xOy và tia Ox đi qua vạch O của thước . Kẻ tia Oz đi qua vạch 63 thì Oz chính là tia phân giác của góc xOy.
Câu 32: Trang 87 - SGK Toán 6 tập 2
Khi nào ta kết luận được tia Ox là tia phân giác của góc xOy? Trong những câu trả lời sau, em hay chọn những câu đúng:
a) \[\widehat{xOt}\]=\[\widehat{yOt}\]
b) \[\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\]
c) \[\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\] và \[\widehat{xOt}=\widehat{tOy}\]
d) \[\widehat{xOt}=\widehat{tOy}\]=\[\frac{1}{2}\widehat{xOy}\]
Lời giải chi tiết
a) Sai vì thiếu Ot nằm giữa Ox và Oy
b) Sai vì thiếu góc xOt = tOy
c) Đúng
d) Đúng
Câu 33: Trang 87 - SGK Toán 6 tập 2
Vẽ hai góc kề bù xOy, yOx', biết \[\widehat{xOy}=\]1300.Gọi Ot là tia phân giác của góc xOy. Tính số đo góc \[\widehat{{x}'Ot}\]
Lời giải chi tiết
Vì Ot là tia phân giác của góc xOy nên \[\widehat{xOt}=\widehat{tOy}=\frac{1}{2}\widehat{xOy}\]=\[\frac{{{130}^{0}}}{2}\]= 650
Vì hai góc xOy, yOx' kề bù nên \[\widehat{xO{x}'}=\widehat{xOy}+\widehat{yO{x}'}={{180}^{0}}\]
\[\widehat{xO{x}'}>\widehat{xOt}({{180}^{0}}>{{65}^{0}})\]
nên tia Ot nằm giữa hai tia Ox và Ox'
Ta có:
\[\widehat{xOt}+\widehat{{x}'Ot}=\widehat{xO{x}'}\]
\[\Rightarrow \widehat{{x}'Ot}=\widehat{xO{x}'}-\widehat{xOt}={{180}^{0}}-{{65}^{0}}={{115}^{0}}\]
Câu 34: Trang 87 - SGK Toán 6 tập 2
Vẽ hai góc kề bù xOy, yOx', biết \[\widehat{xOy}=\] 1000 . Gọi Ot là tia phân giác của góc xOy và Ot' là tia phân giác của góc x'Oy. Tính số đo các góc x'Ot, xOt', tOt'.
Lời giải chi tiết
.png)
Hai góc xOy và x'Oy là hai góc kề bù mà \[\widehat{xOy}=\] 1000 nên \[\widehat{{x}'Oy}\]
= 1800 - 1000 = 800.
Ot là tia phân giác của góc xOy nên \[\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}=\frac{{{100}^{0}}}{2}={{50}^{0}}\]
Ot' là tia phân giác của góc x'Oy nên \[\widehat{{x}'O{t}'}=\widehat{{t}'Oy}=\frac{\widehat{{x}'Oy}}{2}=\frac{{{80}^{0}}}{2}={{40}^{0}}\]
\[\widehat{{x}'Ot}=\widehat{{x}'Oy}+\widehat{tOy}={{80}^{0}}+{{50}^{0}}={{130}^{0}}\]
\[\widehat{xO{t}'}=\widehat{xOy}+\widehat{{t}'Oy}={{100}^{0}}+{{40}^{0}}={{140}^{0}}\]
\[\widehat{tO{t}'}=\widehat{tOy}+\widehat{{t}'Oy}={{50}^{0}}+{{40}^{0}}={{90}^{0}}\]
Câu 35: Trang 87 - SGK Toán 6 tập 2
Vẽ góc bẹt xOy. Vẽ tia phân giác Om của góc đó. Vẽ tia phân giác Oa của góc xOm. Vẽ tia phân giác Ob của góc mOy. Tính số đo góc \[\widehat{{a}'Ob}\].
Lời giải chi tiết
.png)
Vì Om là tia phân giác của góc bẹt xOy => \[\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}={{90}^{{}^\circ }}\]
Vì Oa là tia phân giác của góc \[\widehat{xOm}\] => \[\widehat{xOa}=\widehat{aOm}=\frac{1}{2}.\widehat{xOm}=\frac{1}{2}{{.90}^{{}^\circ }}={{45}^{{}^\circ }}\]
Vì Ob là tia phân giác của góc \[\widehat{yOm}\] => \[\widehat{mOb}=\widehat{bOy}=\frac{1}{2}.\widehat{yOm}=\frac{1}{2}{{.90}^{{}^\circ }}={{45}^{{}^\circ }}\]
Ta có: \[\widehat{xOa}+\widehat{aOb}+\widehat{bOy}={{180}^{0}}\](cộng góc liên tiếp)
=>\[\widehat{aOb}={{180}^{0}}-{{45}^{0}}-{{45}^{0}}={{90}^{0}}\]
Vậy \[\widehat{aOb}={{90}^{0}}\]
Câu 36: Trang 87 - SGK Toán 6 tập 2
Cho hai tia Oy,Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết: \[\widehat{xOy}\] =300,\[\widehat{xOz}\] =800. Vẽ tia phân giác Om của \[\widehat{xOy}\]. Vẽ tia phân giác On của \[\widehat{yOz}\]. Tính \[\widehat{mOn}\]
Lời giải chi tiết
.png)
Vì Om là tia phân giác \[\widehat{xOy}\] => \[\widehat{xOm}=\frac{1}{2}.\widehat{xOy}=\frac{1}{2}{{.30}^{{}^\circ }}={{15}^{{}^\circ }}\]
Vì hai tia Oy,Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox mà \[\widehat{xOy}<\widehat{xOz}\] (do 300<800)
=> Tia Oy nằm giữa hai tia Ox và Oz
=> \[\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\]
=> \[\widehat{yOz}=\widehat{xOz}-\widehat{xOy}={{80}^{0}}-{{30}^{0}}=5\]
Vì On là tia phân giác \[\widehat{yOz}\]=> \[\widehat{nOz}=\frac{1}{2}.\widehat{yOz}=\frac{1}{2}{{.50}^{{}^\circ }}={{25}^{{}^\circ }}\]
Ta có: \[\widehat{xOm}+\widehat{mOn}+\widehat{nOz}=\widehat{xOz}\]
=> \[\widehat{mOn}={{80}^{0}}-{{25}^{0}}-{{15}^{0}}={{40}^{0}}\]
Vậy \[\widehat{mOn}={{40}^{0}}\]
Câu 37: Trang 87 - SGK Toán 6 tập 2
Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết rằng \[\widehat{xOy}\] =300 ,\[\widehat{xOz}\] = 1200.
a) Tính số đo góc yOz.
b) Vẽ tia phân giác Om của \[\widehat{xOy}\], tia phân giác On của \[\widehat{xOz}\]. Tính số đo góc mOn
Lời giải chi tiết
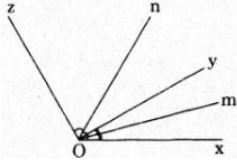
a)
Do hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng bờ chứa tia Ox, mà: \[\widehat{xOy}<\widehat{xOz}\] nên ta có tia Oy nằm giữa hai tia Ox, Oz, từ đó tính được:
\[\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\Rightarrow \widehat{yOz}=\widehat{xOz}-\widehat{xOy}\]
\[\widehat{yOz}\]= 1200- 300= 900
b)Ta có tia Om là tia phân giác của góc xOy nên:
\[\widehat{xOm}=\widehat{yOm}=\frac{\widehat{xOy}}{2}=\frac{{{30}^{0}}}{2}={{15}^{0}}\]
Ta có tia On là tia phân giác của góc xOz nên ta có:
\[\widehat{xOn}=\widehat{nOz}=\frac{\widehat{xOz}}{2}=\frac{{{120}^{0}}}{2}={{60}^{0}}\]
Tia Om nằm giữa hai tia Ox và On, nên ta có:
\[\widehat{xOm}+\widehat{mOn}=\widehat{xOn}\]
\[\Rightarrow \widehat{mOn}=\widehat{xOn}-\widehat{xOm}={{60}^{0}}-{{15}^{0}}={{45}^{0}}\]
