A. Tóm tắt lý thuyết
Muốn nhân hai phân số, ta nhân các tử với nhau, nhân các mẫu với nhau:
\[\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}.\]
Lưu ý:
a) Vì một số nguyên m được coi là phân số \[\frac{m}{1}\] nên
\[m.\frac{a}{b}=\frac{m}{1}.\frac{a}{b}=\frac{m.a}{1.b}=\frac{m.a}{b}.\]
Điều này có nghĩa là: Muốn nhân một số nguyên với một phân số, ta nhân số nguyên đó với tử của phân số và giữ nguyên mẫu.
b) Với n là một số nguyên dương, ta gọi tích của n thừa số \[\frac{a}{b}\] là lũy thừa bậc n của \[\frac{a}{b}\] và kí hiệu là \[{{\left( \frac{a}{b} \right)}^{n}}\]
Theo quy tắc phân số ta có :
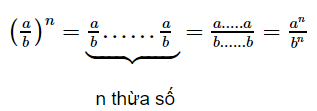
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Bài 69: trang 36 sgk Toán 6 tập 2
Nhân các phân số (rút gọn nếu có thể):
a) \[\frac{-1}{4}.\frac{1}{3}\]
b) \[\frac{-2}{5}.\frac{5}{-9}\]
c) \[\frac{-3}{4}.\frac{16}{7}\]
d) \[\frac{-8}{3}.\frac{15}{24}\]
e) \[(-5).\frac{8}{15}\]
g) \[\frac{-9}{11}.\frac{5}{18}\]
Lời giải chi tiết
a) \[\frac{-1}{4}.\frac{1}{3}=\frac{-1.1}{4.3}\]=\[\frac{-1}{12}\]
b) \[\frac{-2}{5}.\frac{5}{-9}=\frac{-2.5}{5.(-9)}=\frac{2}{9}\]
c) \[\frac{-3}{4}.\frac{16}{17}=\frac{-3.16}{4.17}=\frac{-12}{17}\]
d) \[\frac{-8}{3}.\frac{15}{24}=\frac{-8}{3}.\frac{5}{8}=\frac{-8.5}{3.8}=\frac{-5}{3}\]
e) \[(-5).\frac{8}{15}=\frac{-5.8}{15}=\frac{-8}{3}\]
g) \[\frac{-9}{11}.\frac{5}{18}=\frac{-9.5}{11.18}=\frac{-5}{22}\]
Bài 70: trang 37 sgk Toán 6 tập 2
Phân số \[\frac{6}{35}\] có thể được viết dưới dạng tích của hai phân số có tử và mẫu số là số nguyên dương có một chữ số.
Chẳng hạn: \[\frac{6}{35}=\frac{2}{5}.\frac{3}{7}\]. Hãy tìm cách viết khác.
Lời giải chi tiết
Ta có : 6 = 1 . 6 = 2 . 3; 35 = 5 . 7
Do đó ta có ba cách phân tích khác sau đây:
\[\frac{6}{35}=\frac{1}{5}.\frac{6}{7}\]; \[\frac{6}{35}=\frac{6}{5}.\frac{1}{7}\]; \[\frac{6}{35}=\frac{2}{7}.\frac{3}{5}\]
Bài 71: trang 37 sgk Toán 6 tập 2
Tìm x, biết:
a) \[x-\frac{1}{4}=\frac{5}{8}.\frac{2}{3}\]
b) \[\frac{x}{126}=\frac{-5}{9}.\frac{4}{7}\]
Lời giải chi tiết
a) \[x-\frac{1}{4}=\frac{5}{8}.\frac{2}{3}\]
\[x-\frac{1}{4}=\frac{5}{12}\]
\[x=\frac{5}{12}+\frac{1}{4}\]
\[x=\frac{8}{12}=\frac{2}{3}\]
b) \[\frac{x}{126}=\frac{-5}{9}.\frac{4}{7}\]
\[\frac{x}{126}=\frac{-20}{63}\]
\[63.x=-20.126\]
\[x=\frac{-20.126}{63}\]
\[x=-40\]
Bài 72: trang 37 sgk Toán 6 tập 2
Đố: Có những cặp phân số mà khi ta nhân chúng với nhau hoặc cộng chúng với nhau đều được cùng một kết quả.
Chẳng hạn : Cặp phân số \[\frac{7}{3}\] và \[\frac{7}{4}\] có :
\[\frac{7}{3}.\frac{7}{4}=\frac{7.7}{3.4}=\frac{49}{12}\]
\[\frac{7}{3}+\frac{7}{4}=\frac{7.4+7.3}{3.4}=\frac{49}{12}\]
Đố em tìm được một cặp phân số khác cũng có tính chất ấy.
Lời giải chi tiết
Giả sử ta chọn hai phân số có cùng tử: \[\frac{a}{x}\] và \[\frac{a}{y}.\]
Ta muốn có \[\frac{a}{x}.\frac{a}{y}=\frac{a}{x}+\frac{a}{y}=\frac{ay+ax}{xy}=\frac{a(x+y)}{xy}\]
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
\[\frac{11}{5}+\frac{11}{6}=\frac{11.6+11.5}{5.6}=\frac{121}{30}.\]
Mặt khác, \[\frac{11}{5}.\frac{11}{6}=\frac{11.11}{30}=\frac{121}{30}.\]. Vậy \[\frac{11}{5}.\frac{11}{6}=\frac{11}{5}+\frac{11}{6}\]
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.
