A. Tóm tắt lý thuyết
a) Tính chất giao hoán \[\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{a}{b}.\]
b) Tính chất kết hợp: \[\left( \frac{a}{b}.\frac{c}{d} \right).\frac{p}{q}=\frac{a}{b}.(\frac{c}{d}.\frac{p}{q})\]
c) Nhân với số 1 : \[\frac{a}{b}.1=1.\frac{a}{b}=\frac{a}{b}\]
d) Tính chất phân phối của phép nhân với phép cộng.
\[\frac{a}{b}.\left( \frac{c}{d}+\frac{p}{q} \right)=\frac{a}{b}.\frac{c}{d}+\frac{a}{b}.\frac{p}{q}.\]
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Bài 73: trang 38 sgk Toán 6 tập 2
Trong hai câu sau đây, câu nào đúng ?
Câu thứ nhất : Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu.
Câu thứ hai : Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu.
Lời giải chi tiết
Câu thứ hai đúng. Câu thứ nhất sai.
Bài 74: trang 39 sgk Toán 6 tập 2
Điền các số thích hợp vào bảng sau:
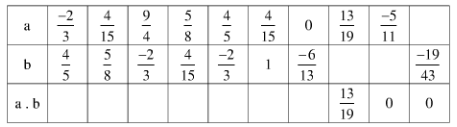
Lời giải chi tiết
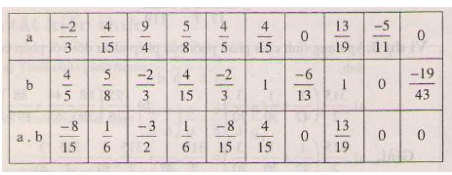
Bài 75: trang 39 sgk Toán 6 tập 2
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể):
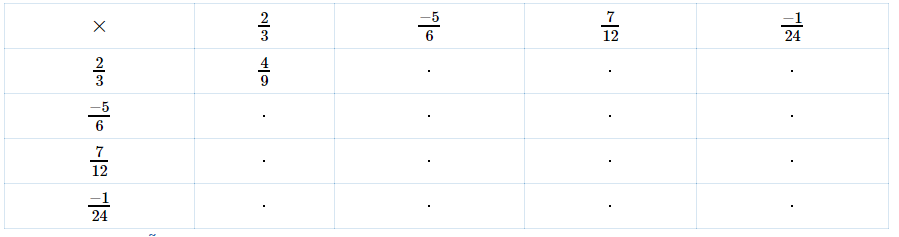
Lời giải chi tiết
Ta nhân lần lượt thu được bảng sau:
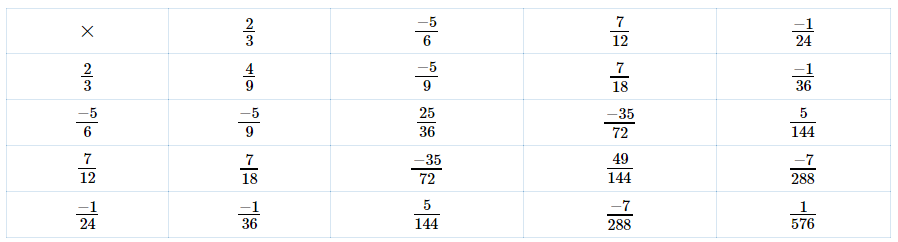
Bài 76: trang 39 sgk Toán 6 tập 2
Tính giá trị biểu thức sau một cách hợp lí:
\[A=\frac{7}{19}.\frac{8}{11}+\frac{7}{19}.\frac{3}{11}+\frac{12}{19}\]
\[B=\frac{5}{9}.\frac{7}{13}+\frac{5}{9}.\frac{9}{13}-\frac{5}{9}.\frac{3}{13}\]
\[C=\left( \frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right).\left( \frac{1}{3}-\frac{1}{4}-\frac{1}{12} \right)\]
Lời giải chi tiết
\[A=\frac{7}{19}.\frac{8}{11}+\frac{7}{19}.\frac{3}{11}+\frac{12}{19}\]
\[A=\frac{7}{19}.\left( \frac{8}{11}+\frac{3}{11} \right)+\frac{12}{19}=\frac{7}{19}.1+\frac{12}{19}=1\]
\[B=\frac{5}{9}.\frac{7}{13}+\frac{5}{9}.\frac{9}{13}-\frac{5}{9}.\frac{3}{13}\]
\[B=\frac{5}{9}.\left( \frac{7}{13}+\frac{9}{13}-\frac{3}{13} \right)=\frac{5}{9}.\frac{7+9-3}{13}=\frac{5}{9}.\frac{13}{13}=\frac{5}{9}.\]
\[C=\left( \frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right).\left( \frac{1}{3}-\frac{1}{4}-\frac{1}{12} \right)\]
\[=\left( \frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right).\frac{4-3-1}{12}\]
\[=\left( \frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right).0=0\]
Bài 77: trang 39 sgk Toán 6 tập 2
Tính giá trị các biểu thức sau:
\[A=a.\frac{1}{2}+a.\frac{1}{3}-a.\frac{1}{4}\] với \[a=\frac{-4}{5}\]
\[B=\frac{3}{4}.b+\frac{4}{3}.b-\frac{1}{2}.b\] với \[b=\frac{6}{19}\]
\[C=c.\frac{3}{4}+c.\frac{5}{6}-c.\frac{19}{12}\] với \[c=\frac{2002}{2003}\]
Lời giải chi tiết
Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn, \[A=a.\left( \frac{1}{2}+\frac{1}{3}-\frac{1}{4} \right)=a.\frac{6+4-3}{12}=a.\frac{7}{12}\]
Với \[a=\frac{-4}{5}\] thì \[A=\frac{-4}{5}.\frac{7}{12}=\frac{-7}{15}.\]
\[B=\frac{3}{4}.b+\frac{4}{3}.b-\frac{1}{2}.b\]
=\[b\left( \frac{3}{4}+\frac{4}{3}-\frac{1}{2} \right)=b.\frac{3.3+4.4-1.6}{12}=b.\frac{19}{12}\]
Với \[b=\frac{6}{19}\Rightarrow B=\frac{6}{19}.\frac{19}{12}=\frac{1}{2}\]
\[C=c.\left( \frac{3}{4}+\frac{5}{6}-\frac{19}{12} \right)\]
\[=c.\left( \frac{3.3}{12}+\frac{5.2}{12}-\frac{19}{12} \right)=c.0=0\]
C = 0
