A.Tóm tắt lý thuyết mở rộng khái niệm về phân số
Người ta gọi \[\frac{a}{b}\] với a, b ∈ Z, b ≠ 0 là một phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số.
Số nguyên a cũng được viết dưới dạng phân số là \[\frac{a}{1}\].
B. Hướng dẫn giải bài tập trong sách giáo khoa
Bài 1 (trang 5 SGK Toán 6 tập 2):
Ta biểu diễn 1/4 của hình tròn bằng cách chia hình tròn thành bốn phần bằng nhau rồi tô màu một phần như hình 1.
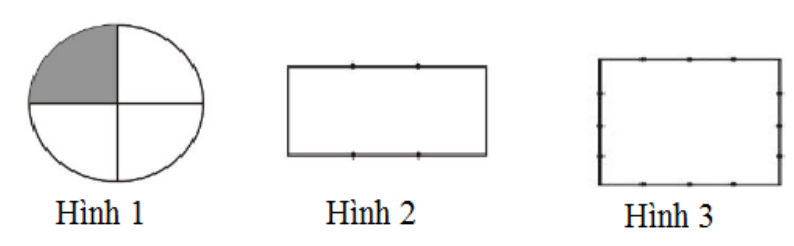
Theo cách đó, hãy biểu diễn:
a) 2/3 của hình chữ nhật.
b) 7/16 của hình vuông.
Lời giải:
a) Tô đậm hai phần ba của hình chữ nhật.

b) Chia hình vuông thành 16 phần rồi tô đậm 7 phần như hình dưới.

Bài 2 (trang 6 SGK Toán 6 tập 2): Phần tô màu trong các hình 4a, b, c, d biểu diễn các phân số nào?
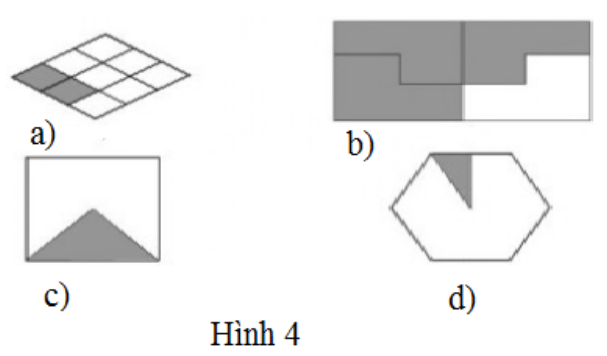
Hướng dẫn:
Hình 4a là một hình vuông được chia thành 9 hình vuông nhỏ bằng nhau, phần tô màu chiếm 2 trong 9 phần đó. Do đó phần tô màu biểu diễn của phân số 2/9. Các phần b, c, d bạn làm tương tự.
Đáp số:
a) Hình a biểu diễn phân số 2/9
b) Hình a biểu diễn phân số 9/12 = 3/4
c) Hình a biểu diễn phân số 1/4
d) Hình a biểu diễn phân số 1/12
Bài 3 (trang 6 SGK Toán 6 tập 2): Viết các phân số sau:
a) Hai phần bảy
b) Âm năm phần chín
c) Mười một phần mười ba
d) Mười bốn phần năm
Lời giải:
a) Hai phần bảy: \[\frac{2}{7}\]
b) Âm năm phần chín: \[\frac{-5}{9}\]
c) Mười một phần mười ba: \[\frac{11}{13}\]
d) Mười bốn phần năm: \[\frac{14}{5}\]
Bài 4 (trang 6 SGK Toán 6 tập 2): Viết các phép chia sau dưới dạng phân số:
a) 3 : 11
b) -4 : 7
c) 5 : (-13)
d) x chia cho 3 (x ∈ Z).
Lời giải
a) \[\frac{3}{11}\]
b) \[\frac{-4}{7}\]
c) \[\frac{5}{-13}\]
d) x chia cho 3 (x ∈ Z) viết là \[\frac{x}{3}\]
Bài 5 (trang 6 SGK Toán 6 tập 2): Dùng cả hai số 5 và 7 để viết thành phân số (mỗi số chỉ được viết một lần ). Cũng hỏi như vậy đối với hai số 0 và -2.
Lời giải
- Dùng cả hai số 5 và 7 để viết thành phân số. Ta được 2 phân số là:
\[\frac{5}{7}\] và \[\frac{7}{5}\]
- Dùng hai số 0 và -2 để viết thành phân số. Ta viết được 1 phân số, vì mẫu số không thể bằng 0, nên phân số viết được là:
\[\frac{0}{2}\]
