Bài 1 (trang 22 sgk Toán 6 Tập 1): Hà Nội, Huế, Nha Trang, Thành phố Hồ Chí Minh nằm trên quốc lộ 1 theo thứ tự như trên. Cho biết các quãng đường trên quốc lộ ấy:
Hà Nội - Huế là 658 km
Hà Nội - Nha Trang là 1278 km
Hà Nội - Thành phố Hồ Chí Minh là 1710 km
Tính các quãng đường Huế - Nha Trang, Nha Trang – Thành phố Hồ Chí Minh.
Lời giải:
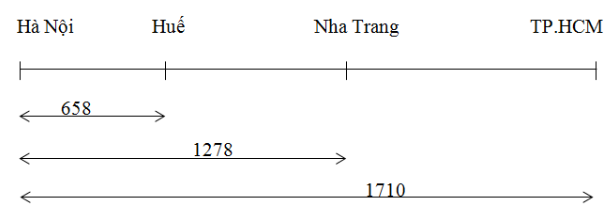
Từ hình trên, các bạn có thể dễ dàng tính được:
- Quãng đường Huế - Nha Trang là: 1278 - 658 = 620 (km)
- Quãng đường Nha Trang - Thành phố Hồ Chí Minh là: 1710 – 1278 = 432 (km)
Bài 2 (trang 23 sgk Toán 6 Tập 1): Các số liệu về kênh đào Xuy–ê (Ai Cập) nối Địa Trung Hải và Hồng Hải được cho trong bảng 1 và bảng 2.
a) Trong bảng 1, các số liệu ở năm 1955 tăng thêm (hay giảm bớt) bao nhiêu so với năm 1869 (năm khánh thành kênh đào)?
b) Nhờ đi qua kênh đào Xuy–ê mỗi hành trình trong bảng 2 giảm bớt được bao nhiêu kilômét?
Bảng 1
|
Kênh đào Xuy–ê |
Năm 1869 |
Năm 1955 |
|
Chiều rộng mặt kênh |
58m |
135m |
|
Chiều rộng đáy kênh |
22m |
50m |
|
Độ sau của kênh |
6m |
13m |
|
Thời gian tàu qua kênh |
48 giờ |
14 giờ |
Bảng 2
|
Hành trình |
Qua mũi Hảo Vọng |
Qua kênh Xuy–ê |
|
Luân Đôn – Bom–bay |
17400km |
10100km |
|
Mác–xây – Bom-bay |
16000km |
7400km |
|
Ô–đét-xa – Bom–bay |
19000km |
6800km |
Lời giải:
a) Từ bảng 1:
- Chiều rộng mặt kênh ở năm 1955 tăng so với năm 1896 là:
135 - 58 = 77 (m)
- Chiều rộng đáy kênh ở năm 1955 tăng so với năm 1896 là:
50 - 22 = 28 (m)
- Độ sâu của kênh ở năm 1955 tăng so với năm 1896 là:
13 - 6 = 7 (m)
- Thời gian tàu qua kênh năm 1955 giảm so với năm 1896 là:
48 - 14 = 34 (giờ)
b) Từ bảng 2:
- Hành trình Luân Đôn – Bom-bay giảm được:
17400 – 10100 = 7300 (km)
- Hành trình Mác-xây – Bom-bay giảm được:
16000 – 7400 = 8600 (km)
- Hành trình Ô-đét-xa – Bom-bay giảm được:
19000 – 6800 = 12200 (km)
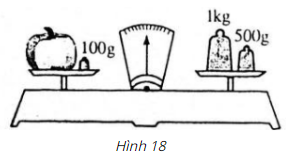
Bài 3 (trang 23 sgk Toán 6 Tập 1): Tính khối lượng của quả bí ở hình 18 khi cân thăng bằng:
Lời giải:
Mặt cân bên trái sẽ có khối lượng là:
khối lượng quả bí + 100 (g)
Mặt cân bên phải có khối lượng là:
1000 + 500 = 1500 (g)
Để cân thăng bằng thì hai mặt cân bên trái - bên phải phải có khối lượng bằng nhau. Do đó:
khối lượng quả bí + 100 = 1500
khối lượng quả bí = 1500 - 100
khối lượng quả bí = 1400 (g)
Vậy để mặt cân thăng bằng thì quả bí phải có khối lượng là 1400 g.
Bài 4 (trang 24 sgk Toán 6 Tập 1): Tìm số tự nhiên x, biết:
a) x : 13 = 41; b) 1428 : x = 14; c) 4x : 17 = 0;
d) 7x - 8 = 713; e) 8(x - 3) = 0; g) 0 : x = 0.
Lời giải:
a) x : 13 = 41
x = 13.41
x = 533 (Áp dụng điều suy ra 2. ở trên)
b)1428 : x = 14
x = 1428 : 14
x = 102
c) 4x : 17 = 0
4x = 0.17
4x = 0
x = 0
Vì x là số chia nên x phải khác 0.
Vì số 0 chia cho mọi số khác 0 đều cho kết quả là 0 nên kết quả của x là bất kì số tự nhiên nào khác 0 hay x ∈ N*
Bài 5 (trang 24 sgk Toán 6 Tập 1): Điền vào ô trống sao cho a = b.q + r với 0 ≤ r < b
|
a |
392 |
278 |
357 |
420 |
|
|
b |
28 |
13 |
21 |
14 |
|
|
q |
25 |
12 |
|||
|
r |
10 |
0 |
Lời giải:
Kết quả:
|
a |
392 |
278 |
357 |
360 |
420 |
|
b |
28 |
13 |
21 |
14 |
35 |
|
q |
14 |
21 |
17 |
25 |
12 |
|
r |
0 |
5 |
0 |
10 |
0 |
Cách làm:
(Số bị chia) = (Số chia) . (Thương) + (Số dư)
a = b . q + r
- Nếu biết a, b thì các bạn lấy a chia cho b sẽ ra Thương và Số dư
- Nếu biết b, q, r thì các bạn thay số vào phép tính b.q + r sẽ cho a
- Nếu biết a, q, r thì các bạn thay số vào phép tính: a = b.q + r để tìm b.
- Cột 1: a = 392, b = 28
Chia 392 cho 28 được q = 14; r = 0
- Cột 2: a = 278; b = 13
Chia 278 cho 13 ta được q = 21; r = 5
- Cột 3: a = 357; b = 21
Chia 357 cho 21 ta được q = 17; r =0
- Cột 4: b = 14; q = 25; r = 10
Vậy a = 14.25 + 10 = 360
- Cột 5: a = 420; b= 12; r = 0
Vậy 420 = b.12 + 0
b = 420 : 12
b = 35
Bài 6 (trang 24 sgk Toán 6 Tập 1):
a) Trong phép chia cho 2, số dư có thể bằng 0 hoặc bằng 1. Trong phép chia cho 3, cho 4, cho 5, số dư có thể bằng bao nhiêu?
b) Dạng tổng quát của số chia hết cho 2 là 2k, dạng tổng quát của số chia hết cho 2 dư 1 là 2k + 1 với k thuộc N. Hãy viết dạng tổng quát của số chia hết cho 3, chia cho 3 dư 1, số chia cho 3 dư 2.
Lời giải:
a)
- Trong phép chia cho 3, số dư có thể bằng: 0, 1, 2
- Trong phép chia cho 4, số dư có thể bằng: 0, 1, 2, 3
- trong phép chia cho 5, số dư có thể bằng: 0, 1, 2, 3, 4
Giải thích chi tiết: Trong phép chia a cho b, số dư r phải thỏa mãn điều kiện 0 <= r < b. Nói cách khác, số dư luôn luôn lớn hơn hoặc bằng 0 và luôn nhỏ hơn Số chia.
b) Dạng tổng quát
của số chia hết cho 3 là 3k
của số chia cho 3 dư 1 là 3k + 1
của số chia cho 3 dư 2 là 3k + 2
với điều kiện của k như trong đề bài
