Bài 1 trang 97 SGK Hình học 11: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) \[\overrightarrow{AB}\] và \[\overrightarrow{EG};\]
b) \[\overrightarrow{AF}\] và \[\overrightarrow{EG};\]
c) \[\overrightarrow{EG};\] và \[\overrightarrow{DH}.\]
Lời giải
.png)
a) \[(\widehat{\overrightarrow{AB},\overrightarrow{EG}})\] \[=(\widehat{\overrightarrow{AB},\overrightarrow{AC}})\]\[={{45}^{0}};\]
b) \[\widehat{(\overrightarrow{AF},\overrightarrow{EG})}==\widehat{(\overrightarrow{DG},\overrightarrow{EG})}=={{60}^{0}};\] (Vì tam giác DGE là tam giác đều)
c) \[(\widehat{\overrightarrow{AB},\overrightarrow{DH}})={{90}^{0}}.\] Vì \[DH\bot (ABCD)\]
Bài 2 trang 97 SGK Hình học 11.
Cho hình tứ diện ABCD.
Chứng minh rằng: \[\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0.\]
Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có \[AB\bot CD\] và \[AC\bot DB\] thì \[AD\bot BC\]
Lời giải
a) \[\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})\]
\[\overrightarrow{AC}.\overrightarrow{DB}=\overrightarrow{AC}.(\overrightarrow{AB}-\overrightarrow{AD})\]
\[\overrightarrow{AD}.\overrightarrow{BC}=\overrightarrow{AD}.(\overrightarrow{AC}-\overrightarrow{AB}).\]
Cộng từng vế ba đẳng thức trên ta được đẳng thức phải chứng minh.
b) \[AB\bot CD\Rightarrow \overrightarrow{AB}.\overrightarrow{CD}=0,\]
\[AC\bot DB\Rightarrow \overrightarrow{AC}.\overrightarrow{DB}=0\]
Từ đẳng thức câu a ta có:
\[\Rightarrow \overrightarrow{AD}.\overrightarrow{BC}=0\Rightarrow AD\bot BC\]
Bài 3 (trang 97 SGK Hình học 11):
a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a và b có song song với nhau không?
b) Trong không gian nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a có vuông góc với c không?
Lời giải:
a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì nói chung a và b không song song với nhau vì a và b có thể cắt nhau hoặc có thể chéo nhau.
b) Trong không gian nếu a ⊥ b và b ⊥ c thì a và c vẫn có thể cắt nhau hoặc chéo nhau do đó, nói chung a và c không vuông góc với nhau.
Bài 4 (trang 98 SGK Hình học 11): Cho hai tam giác đều ABC và ABC' trong không gian nói chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AC, CB, BC' và C'A.
Chứng minh rằng:
a) AB ⊥ CC'
b) Tứ giác MNPQ là hình chữ nhật.
Lời giải:
.png)
a) \[\overrightarrow{AB}.\overrightarrow{C{C}'}=\overrightarrow{AB}.(\overrightarrow{A{C}'}-\overrightarrow{AC})\]
\[=\overrightarrow{AB}.\overrightarrow{A{C}'}-\overrightarrow{AB}.\overrightarrow{AC})\]
\[=AB.AC\prime .cos{{60}^{0}}-AB.AC.cos{{60}^{0}}=0\]
\[\Rightarrow AB\bot C{C}'\]
b) Theo giả thiết Q,P là trung điểm của AC′,BC′ do đó QP là đường trung bình của tam giác ABC′
Suy ra: \[QP//AB,QP=\frac{1}{2}AB\] (1)
Chứng minh tương tự ta có:
\[PN//C{C}',PN=\frac{1}{2}C{C}'\]
\[MN//AB,MN=\frac{1}{2}AB\] (2)
Từ (1) và (2) suy ra: \[MN//QP,MN=QP\]; Do đó MNPQ là hình bình hành.
Ta có: \[MN//AB\], \[PN//C{C}'\] mà \[AB\bot C{C}'\] do đó \[MN\bot NP\]
Hình bình hành MNPQ có một góc vuông nên MNPQ là hình chữ nhật.
Bài 5 trang 98 SGK Hình học 11.
Câu 5: Trang 98 - SGK Hình học 11
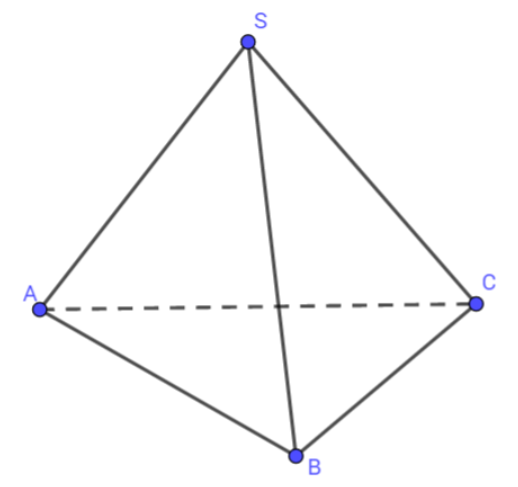
Cho hình chóp tam giác S.ABC có SA=SB=SC và có \[\widehat{ABC}=\widehat{BSC}=\widehat{CSA}.\] Chứng minh rằng SA⊥BC,SB⊥AC,SC⊥AB.
Lời giải:
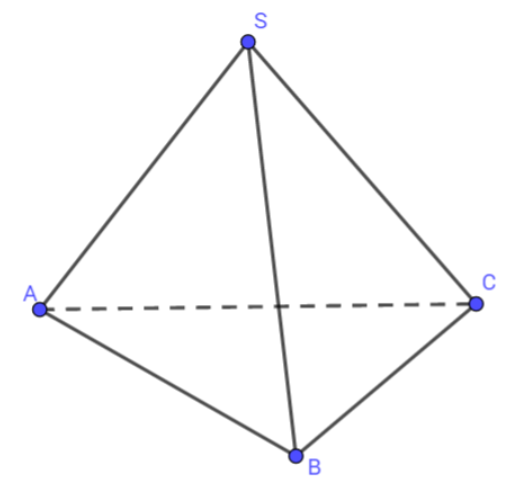
\[\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB})\] \[=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\]
\[=SA.SC.\cos \widehat{ASC}-SA.SB.\cos \widehat{ASB}=0\]
Vậy SA⊥BC
\[\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\]
\[=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\]
\[=SB.SC.\cos \widehat{BSC}-SB.SA.\cos \widehat{ASB}=0\]
Vậy SB⊥AC
\[\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\]=\[=SC.SB.\cos \widehat{BSC}-SC.SA.\cos \widehat{ASC}=0\]
Vậy SC⊥AB
Bài 6 trang 98 SGK Hình học 11.
Trong không gian cho hai hình vuông ABCD và ABC′D′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O′. Chứng minh rằng AB⊥OO′ và tứ giác CDD′C′ là hình chữ nhật.
Lời giải
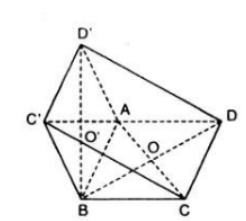
Gọi cạnh của hai hình vuông bằng nhau ABCD và ABC'D" là a.
Ta có: \[\overrightarrow{AB}.\overrightarrow{O{O}'}=\overrightarrow{AB}.(\overrightarrow{A{O}'}-\overrightarrow{AO})\]
\[=AB.A{O}'.cos\widehat{AB{O}'}-AB.AO.cos\widehat{ABO}\]
\[=a.a.\cos {{45}^{0}}-a.a.\cos {{45}^{0}}\]
=0
Vậy AB⊥OO′.
Ta có \[\overrightarrow{CD}.\overrightarrow{C{C}'}=\overrightarrow{CD}.(\overrightarrow{A{C}'}-\overrightarrow{AC})\]
\[=CD.A{C}'.cos\widehat{A{C}'D}-CD.AC.cos\widehat{A{C}'{D}'}\]
\[=a.a.\cos {{45}^{0}}-a.a.\cos {{45}^{0}}\]
=0
> CD⊥CC′ (1)
- Mặt khác: CD song song và bằng C′D′ (do ABCD và ABC'D' là hai hình vuông bằng nhau)
=> CDD′C′ là hình bình hành (2)
Từ (1) (2) => CDD′C′ là hình chữ nhật.
Bài 7 trang 98 SGK Hình học 11.
Cho S là diện tích tam giác ABC. Chứng minh rằng: \[S=\frac{1}{2}\sqrt{{{\overrightarrow{AB}}^{2}}.{{\overrightarrow{AC}}^{2}}-{{(\overrightarrow{AB}.\overrightarrow{AC})}^{2}}}.\]
Lời giải
\[{{S}_{ABC}}=\frac{1}{2}AB.AC.sinA=\frac{1}{2}AB.AC.\sqrt{1-co{{s}^{2}}A}\]
\[=\frac{1}{2}AB.AC.\sqrt{1-{{\left( \frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|} \right)}^{2}}}\]
\[=\frac{1}{2}\sqrt{{{\overrightarrow{AB}}^{2}}.{{\overrightarrow{AC}}^{2}}-{{(\overrightarrow{AB}.\overrightarrow{AC})}^{2}}}.\]
Bài 8 trang 98 SGK Hình học 11.
Cho tứ diện ABCD có AB=AC=AD và \[\widehat{BAC}=\widehat{BAD}={{60}^{0}}.\]
Chứng minh rằng:
a) AB⊥CD;
b) Nếu M,N lần lượt là trung điểm của AB và CD thì MN⊥AB và MN⊥CD.
Lời giải
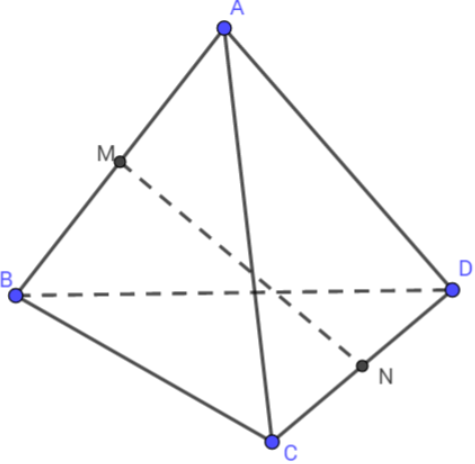
a) \[\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}(\overrightarrow{AD}-\overrightarrow{AC})\]
\[=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\]
\[=AB.AD.\cos \widehat{BAD}-AB.AC.\cos \widehat{BAC}=0\]
\[\Rightarrow AB\bot CD\]
b) \[\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN},\](1)
\[\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\] (2)
Cộng (1) với (2) theo vế với vế ta được: \[\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{BC})=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AC}-\overrightarrow{AB}).\]
Ta có \[\overrightarrow{AB}.\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AB}.(\overrightarrow{AD}+\overrightarrow{AC}-\overrightarrow{AB})\]
\[=\frac{1}{2}(\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AB}.\overrightarrow{AC}-A{{B}^{2}})\]
\[=\frac{1}{2}(AB.AD.\cos \widehat{BAD}+AB.AC.\cos \widehat{BAC}-A{{B}^{2}}\]
\[=\frac{1}{2}(AB.AD.\cos {{60}^{0}}+AB.AC.\cos {{60}^{0}}-A{{B}^{2}})\]
\[=\frac{1}{2}\left( \frac{1}{2}A{{B}^{2}}+\frac{1}{2}A{{B}^{2}}-A{{B}^{2}} \right)=0\]\[\Rightarrow AB\bot MN\]
Chứng minh tương tự ta được: CD⊥MN