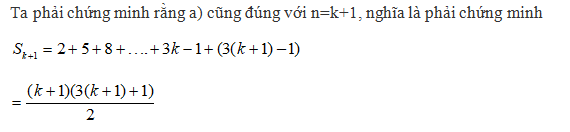Câu 1: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với n Є N*, ta có đẳng thức:
a) \[2+5+8+....+3n-1=\frac{n(3n+1)}{2}\]
b) \[\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{n}}}=\frac{{{2}^{n}}-1}{{{2}^{n}}}\]
c) \[{{1}^{2}}+{{2}^{2}}+{{3}^{2}}+...+{{n}^{2}}=\frac{n(n+1)(2n+1)}{6}\]
Lời giải
a) Với n=1, vế trái chỉ có một số hạng là 2, vế phải bằng \[\frac{1.(3.1+1)}{2}=2\] . Do đó hệ thức a) đúng với n=1.
Đặt vế trái bằng Sn
Giả sử đẳng thức a) đúng với \[n=k\ge 1\], tức là
\[{{S}_{k}}=2+5+8+\ldots +3k1=\frac{k(3k+1)}{2}\]
Ta phải chứng minh rằng a) cũng đúng với n=k+1, nghĩa là phải chứng minh
\[{{S}_{k+1}}=2+5+8+\ldots .+3k-1+(3(k+1)1)\]
\[=\frac{(k+1)(3(k+1)+1)}{2}\]
Thật vậy, từ giả thiết quy nạp, ta có: \[{{S}_{k+1}}={{S}_{k}}+3k+2\] = \[\frac{k(3k+1)}{2}+3k+2\]
\[=\frac{3{{k}^{2}}+k+6k+4}{2}\]\[=\frac{3({{k}^{2}}+2k+1)+k+1}{2}=\frac{(k+1)(3(k+1)+1)}{2}\] (điều phải chứng minh)
Vậy theo nguyên lí quy nạp toán học, hệ thức a) đúng với mọi n∈N∗
b) Với n = 1, 2 về của hệ thức bằng nhau.
Đặt vế trái bằng Sn.
Giả sử n = k ≥ 1, tức là \[{{S}_{k}}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{k}}}=\frac{{{2}^{k}}-1}{{{2}^{k}}}\]
Xét với n = k + 1 ta có \[{{S}_{k+1}}={{S}_{k}}+\frac{1}{{{2}^{k+1}}}=\frac{{{2}^{k}}-1}{{{2}^{k}}}+\frac{1}{{{2}^{k+1}}}\]\[=~\frac{{{2}^{k+1}}-2+1}{{{2}^{k+1}}}=\frac{{{2}^{k+1}}-1}{{{2}^{k+1}}}\]
(đpcm)
=>hệ thức b) đúng với mọi n ∈ N*
c) Với n = 1, vế trái bằng về phải. Đặt vế trái bằng Sn.
Giả sử hệ thức đúng với n = k ≥ 1, hay
Sk = 12 + 22 + 32 + …+ k2 = \[\frac{k(k+1)(2k+1)}{6}\]
Xét n = k + 1 ta có
Sk+1 = Sk + (k + 1)2 \[=\frac{k(k+1)(2k+1)}{6}+{{(k+1)}^{2}}\]
\[=\frac{(k+1)(2k(k+2)+3)+3(k+2)}{6}=\frac{(k+1)(k+2)(2(k+1)+1)}{6}\](đpcm)
=>hệ thức c) đúng với mọi n ∈ N*
Câu 2: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với n ∈ N* ta luôn có:
a) n3 + 3n2 + 5n chia hết cho 3;
b) 4n + 15n - 1 chia hết cho 9;
c) n3 + 11n chia hết cho 6.
Lời giải
a) Đặt Sn = n3 + 3n2 + 5n
Với n = 1 thì S1 = 9 chia hết cho 3
Giả sử với n = k ≥ 1, có Sk = (k3 + 3k2 + 5k) ⋮ 3
Xét với n = k + 1
Sk+1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3k2 + 6k + 3 + 5k + 5
= k3 + 3k2 + 5k + 3k2 + 9k + 9
hay Sk+1 = Sk + 3(k2 + 3k + 3)
mà Sk ⋮ 3, 3(k2 + 3k + 3) ⋮ 3 nên Sk+1 ⋮ 3.
Vậy (n3 + 3n2 + 5n) ⋮ 3 với mọi n ε N* .
b) Đặt Sn = 4n + 15n - 1
Với n = 1, thì S1 ⋮ 9
Giả sử với n = k ≥ 1 có Sk= 4k + 15k - 1 chia hết cho 9.
Xét với n = k + 1
Sk+1 = 4k + 1 + 15(k + 1) – 1
= 4(4k + 15k – 1) – 45k + 18 = 4Sk – 9(5k – 2)
mà Sk ⋮ 9 và 9(5k - 2) ⋮ 9 => Sk+1 ⋮ 9
Vậy (4n + 15n - 1) ⋮ 9 với mọi n ∈ N*
c) Đặt Sn = n3 + 11n
Với n = 1 thì S1 ⋮ 6
Giả sử với n = k ≥ 1 có Sk = k3 + 11k ⋮ 6
Xét với n = k + 1 ta có:
Sk+1 = (k + 1)3 + 11(k + 1) = k3 + 3k + 3k + 1 + 11k + 11
= ( k3 + 11k) + 3(k2 + k + 4) = Sk + 3(k2 + k + 4)
mà Sk ⋮ 6, mặt khác k2 + k + 4 = k(k + 1) + 1 là số chẵn nên 3(k2 + k + 4) ⋮ 6 => Sk+1 ⋮ 6
Vậy n3 + 11n chia hết cho 6 với mọi n ∈ N*
Câu 3: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:
a) 3n > 3n + 1;
b) 2n + 1 > 2n + 3
. Lời giải
a) Với n = 2 ta thấy bất đẳng thức đúng
Giả sử bất đẳng thức đúng với n = k ≥ 2, hay 3k > 3k + 1 (*)
Nhân hai vế của (*) với 3, ta được:
3k + 1 > 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1 > 0 => 3k + 1 > 3k + 4 hay 3k + 1 > 3(k + 1) + 1.
=> bất đẳng thức đúng với n = k + 1.
Vậy 3n > 3n + 1 với mọi số tự nhiên n ≥ 2.
b) Ta thấy với n = 2 thì bất đẳng thức đúng
Giả sử bất đẳng thức đúng với n = k ≥ 2 hay 2k + 1 > 2k + 3 (**)
Nhân hai vế của bất đẳng thức (**) với 2, ta được:
2k + 2 > 4k + 6 <=> 2k + 2 > 2k +5 + 2k + 1.
Vì 2k + 1> 0 nên 2k + 2 > 2k + 5
Vậy 2n + 1 > 2n + 3 với mọi số tự nhiên n ≥ 2.
Câu 4: Trang 83 - sgk đại số và giải tích 11
Cho tổng \[{{S}_{n}}=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n(n+1)}\] với n∈N∗.
a) Tính S1, S2, S3.
b) Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
. Lời giải
a) Ta có: \[{{S}_{1}}=\frac{1}{1.2}=\frac{1}{2}\]
\[{{S}_{2}}=\frac{1}{1.2}+\frac{1}{2.3}=\frac{2}{3}\]
\[{{S}_{3}}=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}=\frac{3}{4}\]
b) Từ câu a) ta dự đoán \[{{S}_{n}}=\frac{n}{n+1}(1)\] với mọi n∈N∗.
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n=1, vế trái là \[{{S}_{1}}=\frac{1}{2}\] vế phải bằng \[\frac{1}{1+1}=\frac{1}{2}\]. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n≥1, tức là
\[{{S}_{k}}=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{k(k+1)}=\frac{k}{k+1}\]
Ta phải chứng minh đẳng thức đúng với n=k+1, nghĩa là phải chứng minh
\[{{S}_{k+1}}=\frac{k+1}{k+2}\]
Ta có : \[{{S}_{k+1}}={{S}_{k}}+\frac{1}{(k+1)(k+2)}=\frac{k}{k+1}+\frac{1}{(k+1)(k+2)}\]\[=\frac{{{k}^{2}}+2k+1}{(k+1)(k+2)}=\frac{k+1}{k+2}\]
tức là đẳng thức (1) đúng với n=k+1.
Vậy đẳng thức (1) đã được chứng minh.
Câu 5: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là \[\frac{n(n-3)}{2}\]
Lời giải
Số đoạn thẳng (cả cạnh và đường chéo) trong một đa giác lồi n cạnh là \[C_{2}^{n}\] đoạn thẳng. Suy ra số đường chéo của đa giác lồi có n cạnh là:
\[C_{2}^{n}-n=\frac{n!}{2!(n-2)!}-n=\frac{n(n-2)}{2}-n=\frac{{{n}^{2}}-3n}{2}=\frac{n(n-3)}{2}\](đpcm)