Bài 1 (trang 119 SGK Hình học 11): Trong các mệnh đề sau đây mệnh đề nào là đúng?
a) Đường thẳng Δ là đường vuông góc chung của hai đường thẳng a và b nếu Δ ⊥a và Δ ⊥b.
b) Gọi (P) là mặt phẳng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với (P).
c) Gọi Δ là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì Δ là giao tuyến của hai mặt phẳng (a, Δ) và (b, Δ).
d) Cho hai đường thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Đường vuông góc chung Δ của hai đường thẳng chéo nhau a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
Lời giải:
a) Sai, đúng là "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥a và Δ ⊥b"
b) Đúng
c) Đúng
d) Sai
e) Sai.
Bài 2 (trang 119 SGK Hình học 11): Cho tứ diện S.ABCD có SA vuông góc với mặt phẳng
a) Chứng minh ba đường thẳng AH, SK, BC đồng quy.
b) Chứng minh rằng SC vuông góc với mặt phẳng (BHK) và HK vuông góc với mặt phẳng (SBC).
c) Xác định đường vuông góc chung của BC và SA.
Lời giải:
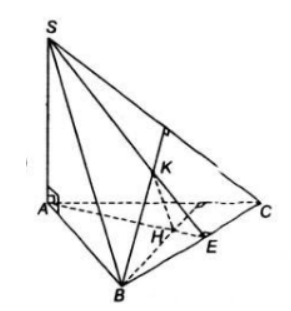
a) Chứng minh AH,SK,BC đồng qui
Trong (ABC), gọi E=AH∩BC.
H là trực tâm của tam giác ABC nên AE⊥BC (1)
SA⊥(ABC)⇒SA⊥BC (2)
Từ (1) và (2) suy ra BC⊥(SAE)⇒BC⊥SE.
Vì K là trực tâm của tam giác SBC(gt)⇒SE đi qua K ⇒AH,BC,SK đồng quy tại E.
b) Chứng minh SC⊥(BHK),HK⊥(SBC)
Vì H là trực tâm tam giác ABC nên BH⊥AC. (3)
Mà AC là hình chiếu vuông góc của SA lên (ABC) (do SA⊥(ABC)−gt)
=> BH⊥SC (định lý ba đường vuông góc) (4)
Từ (3) và (4) suy ra: SC⊥(BHK).
Ta có: SC⊥(BHK),SC⊂(SBC)=>(BHK)⊥(SBC) (5)
Vì: BC⊥(SAE)−cmt,BC⊂(SBC)=>(SAE)⊥(SBC) (6)
Từ (5) (6) và (SAE)∩(BHK)=HK => HK⊥(SBC)
c) Xác định đường vuông góc chung của BC,SA
Ta có: AE⊥BC (tính chất trực tâm H của tam giác ABC)
mặt khác: SA⊥(ABC)⇒SA⊥AE
⇒AE là đường vuông góc chung của BC và SA.
Bài 3 (trang 119 SGK Hình học 11): Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
Lời giải:
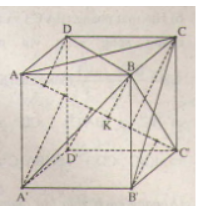
Gọi K là hình chiếu của B trên AC′.
Xét tam giác ABC′ vuông tại B, ta có: BK⊥AC′
=> \[\frac{1}{B{{K}^{2}}}=\frac{1}{B{{A}^{2}}}+\frac{1}{B{{C}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{(a\sqrt{2})}^{2}}}=\frac{3}{2{{a}^{2}}}\]
\[\Rightarrow BK=\frac{a\sqrt{6}}{3}.\]
Ta có:
ΔABC′=ΔC′CA=ΔADC′=ΔAA′C′=ΔC′B′A=ΔC′D′A(c.g.c)
Do đó khoảng cách từ B,C,D,A′,B′,D′ tới AC′ đều bằng \[\frac{a\sqrt{6}}{3}\] vì chúng đều là chiều cao của các tam giác vuông bằng nhau.
Bài 4 (trang 119 SGK Hình học 11): Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c.
Lời giải:
.png)
a) Trong (ABCD) kẻ BH vuông góc với AC (1)
- Vì: CC′⊥(ABCD)⇒CC′⊥BH (2)
Từ (1) và (2) suy ra BH⊥(ACC′A′).
- BH là đường cao trong tam giác vuông ABC nên ta có:
\[BK=\frac{1}{B{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{B{{C}^{2}}}.\] (hệ thức lượng trong tam giác vuông)
\[\Rightarrow BH=\frac{ab}{\sqrt{{{a}^{2}}+{{b}^{2}}}}.\]
b) AC′⊂(ACC′A′), mà BB′//(ACC′A′) ⇒d(BB′,AC′)=d(B,(ACC′A′))
Vì: BH⊥(ACC′A′) nên \[d(B,(AC{C}'{A}')=BH=\frac{ab}{\sqrt{{{a}^{2}}+{{b}^{2}}}}.\]
\[d(B{B}',A{C}')=\frac{ab}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Bài 5 (trang 119 SGK Hình học 11): Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD)
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Lời giải:
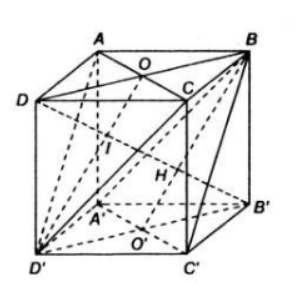
a) Có B′A′=B′B=B′C′⇒B′ thuộc trục của tam giác A′BC′. (1)
DA′=DB=DC′ (đường chéo các hình vuông bằng nhau) ⇒D cũng thuộc trục của tam giác A′BC′ (2)
Từ (1) và (2) suy ra B′D thuộc trục của (A′BC′)
⇒B′D vuông góc với (A′BC′).
b) Chứng minh tương tự ta được B′D⊥(ACD′)
Hai mặt phẳng (BA′C′) và (ACD′) cùng vuông góc với B′D (tại I và H) nên chúng song song với nhau và khoảng cách giữa chúng bằng IH.
Ta có:
O′I//D′H, O′ là trung điểm của B′D′ nên theo định lí Ta lét thì I là trung điểm của B′H hay IB′=IH (3)
OH//IB, O là trung điểm của BD nên theo định lí Ta lét thì H là trung điểm của DI hay HI=HD (4)
Từ (3) và (4) suy ra: \[IH=\frac{{B}'D}{3}=\frac{a\sqrt{3}}{3}\]
c) BC′⊂(BA′C′); CD′⊂(ACD′), mà hai mặt phẳng này song song
Do đó, \[d(B{C}',C{D}')=d((B{A}'{C}'),(AC{D}'))=\frac{a\sqrt{3}}{3}.\]
(Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó).
Bài 6 (trang 119 SGK Hình học 11): Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
Lời giải:
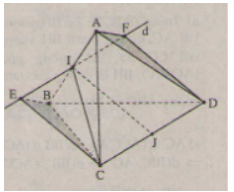
Gọi I là trung điểm AB, J là trung điểm CD.
Qua I kẻ đường thẳng d//CD, lấy trên d điểm E,F sao cho IE=IF=CD2 (I là trung điểm của EF). IJ vuông góc với CD ⇒IJ vuông góc với EF, mà IJ cũng vuông góc với AB⇒IJ⊥(AEBF).
Ta có CDFE là hình bình hành có IJ là đường trung bình
Do đó CE và DF cùng song song với IJ
Vì IJ⊥(AEBF)−cmt
Suy ra CE và DF cùng vuông góc với mp (AEBF)
⇒DF⊥AF,CE⊥IE.
ΔAIF=ΔBIE(c.g.c) suy ra: AF=BE
Xét ∆DFA và ∆CEB có:
+) \[\hat{E}=\hat{F}(={{90}^{0}})\]
+) AF=BE
+) DF=CE
⇒∆DFA=∆CEB(c.g.c)
⇒AD=BC.
Chứng minh tương tự ta được BD=AC.
Bài 7 (trang 120 SGK Hình học 11): Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
Lời giải:
.png)
Gọi H là trực tâm tam giác ABC.
Vì chóp S.ABC đều nên SH⊥(ABC)
=> d(S,(ABC))=SH
Gọi I là trung điểm của BC.
Tam giác ABC đều nên \[AI=\frac{3a\sqrt{3}}{2}\]
\[AH=\frac{2}{3}AI=a\sqrt{3}\]
Áp dung định lí Pytago vào tam giác vuông SAH ta có:
\[S{{A}^{2}}=S{{H}^{2}}+A{{H}^{2}}\]
=>\[SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{4{{a}^{2}}-{{(a\sqrt{3})}^{2}}}=a.\]
Vậy khoảng cách từ S đến mặt phẳng (ABC) bằng a.
Bài 8 (trang 120 SGK Hình học 11): Cho tứ diện ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối diện của tứ diện đều đó.
Lời giải:
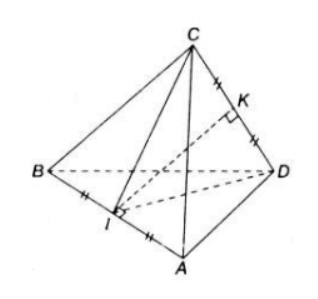
Gọi I là trung điểm AB và K là trung điểm CD.
ΔCBA và ΔDBA là hai tam giác đều cạnh a, có CI,DI lần lượt là trung tuyến ứng với cạnh AB
=> CI=DI (trung tuyến tương ứng của hai tam giác bằng nhau)
=> ΔICD cân tại I có IK là trung tuyến ứng với cạnh CD
=> IK đồng thời là đường cao
=> IK⊥CD. (1)
Chứng minh tương tự: KB=KA=>ΔKAB cân tại K
=> KI vừa là trung tuyến ứng với cạnh AB vừa là đường cao
=> KI⊥AB. (2)
Từ (1)(2) suy ra IK là đoạn vuông góc chung của AB,CD.
Xét tam giác IKC vuông tại K có:
\[C{{I}^{2}}=I{{K}^{2}}+C{{K}^{2}}\] (định lý Pitago)
=> \[IK=\sqrt{C{{I}^{2}}-C{{K}^{2}}}=\sqrt{\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{2}}{2}\]
