Câu 1: trang 141 sgk toán Đại số và giải tích 11
Hãy lập bảng liệt kê các giới hạn đặc biệt của dãy số và các giới hạn đặc biệt của hàm số
Lời giải
Một số giới hạn đặc biệt của dãy số
\[\underset{n\to +\infty }{\mathop{lim}}\,\frac{1}{n}=0\], \[\underset{n\to +\infty }{\mathop{lim}}\,\frac{1}{{{n}^{k}}}=0\] với k nguyên dương;
\[\underset{n\to +\infty }{\mathop{lim}}\,{{q}^{n}}=0\] nếu |q|<1;
Nếu \[{{u}_{n}}=c\] (c là hằng số) thì \[\underset{n\to +\infty }{\mathop{lim}}\,{{u}_{n}}=\underset{n\to +\infty }{\mathop{lim}}\,c=c\]
\[lim{{n}^{k}}=+\infty \] với k nguyên dương;
\[lim{{q}^{n}}=+\infty \] nếu q>1
Một số giới hạn đặc biệt của hàm số
\[\underset{x\to +\infty }{\mathop{lim}}\,{{x}^{k}}=+\infty \] với k nguyên dương.
\[\underset{x\to -\infty }{\mathop{lim}}\,{{x}^{k}}=-\infty \] nếu k là số lẻ
\[\underset{x\to -\infty }{\mathop{lim}}\,{{x}^{k}}=+\infty \] nếu k là số chẵn
\[\underset{x\to +\infty }{\mathop{lim}}\,c=c\]
\[\underset{x\to -\infty }{\mathop{lim}}\,c=c\]
\[\underset{x\to -\infty }{\mathop{lim}}\,\frac{c}{{{x}^{k}}}=0\]
Câu 2: trang 141 sgk toán Đại số và giải tích 11
Cho hai dãy số (un) và (vn). Biết |un–2|≤vn với mọi n và limvn=0.
Có kết luận gì về giới hạn của dãy số (un)?
Lời giải
Với mọi n∈N∗ , ta có:
\[~|{{u}_{n}}-2|={{v}_{n}}\Leftrightarrow -{{v}_{n}}={{u}_{n}}-2={{v}_{n}}\]
Ta lại có \[\underset{n\to +\infty }{\mathop{lim}}\,(-{{v}_{n}})=\underset{n\to +\infty }{\mathop{lim}}\,{{v}_{n}}=0\] nên
\[\underset{n\to +\infty }{\mathop{lim}}\,({{u}_{n}}-2)=0?\underset{n\to +\infty }{\mathop{lim}}\,{{u}_{n}}-lim2=0?\underset{n\to +\infty }{\mathop{lim}}\,{{u}_{n}}=2\]
Vậy \[\underset{n\to +\infty }{\mathop{lim}}\,{{u}_{n}}=2\]
Câu 3: trang 141 sgk toán Đại số và giải tích 11
Tên của một học sinh được mã hóa bởi số 1530. Biết rằng mỗi chữ số trong số này là giá trị của một trong các biểu thức A,H,N,O với:
\[A=\lim \frac{3n-1}{n+2}\]
\[H=\lim (\sqrt{{{n}^{2}}+2n}-n)\]
\[N=\lim \frac{\sqrt{n}-2}{3n+7}\]
\[O=\lim \frac{{{3}^{n}}-{{5.4}^{n}}}{1-4n}\]
Hãy cho biết tên của học sinh này, bằng cách thay các chữ số trên bởi các chữ kí hiệu biểu thức tương ứng
Lời giải
\[A=\lim \frac{3n-1}{n+2}=\lim \frac{n(3-\frac{1}{n})}{n(1+\frac{2}{n})}=\lim \frac{3-\frac{1}{n}}{1+\frac{2}{n}}=\frac{3}{1}=3\]
\[H=\lim (\sqrt{{{n}^{2}}+2n}-n)=\lim \frac{({{n}^{2}}+2n)-{{n}^{2}}}{\sqrt{{{n}^{2}}+2n}+n}\]
\[=\lim \frac{2n}{n\left[ \sqrt{1+\frac{2}{n}}+1 \right]}=\lim \frac{2}{\sqrt{1+\frac{2}{n}}+1}=\frac{2}{1+1}=1\]
\[N=\lim \frac{\sqrt{n}-2}{3n+7}=\lim \frac{n(\sqrt{\frac{1}{n}}-\frac{2}{n})}{n(3+\frac{7}{n})}\]
\[=\lim \frac{\sqrt{\frac{1}{n}}-\frac{2}{n}}{3+\frac{7}{n}}=\frac{0}{3+0}=0\]
\[O=\lim \frac{{{3}^{n}}-{{5.4}^{n}}}{1-4n}=\lim \frac{{{4}^{n}}\left[ {{(\frac{3}{4})}^{n}}-5 \right]}{{{4}^{n}}\left[ {{(\frac{1}{4})}^{n}}-1 \right]}\]
\[=\lim \frac{{{(\frac{3}{4})}^{n}}-5}{{{(\frac{1}{4})}^{n}}-1}=\frac{5}{1}=5\]
Vậy số 1530 là mã số của chữ Hoan.
Câu 4: trang 142 sgk toán Đại số và giải tích 11
a) Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn.
b) Cho ví dụ về cấp số nhân lùi vô hạn có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của mỗi cấp số nhân đó.
Lời giải
a) Công bội q của cấp số nhân lùi vô hạn phải thoản mãn điều kiện |q|<1
b) Ví dụ:
- Cấp số nhân lùi vô hạn có số hạng đầu \[{{u}_{1}}=\text{ }1\] và công bội âm là: \[q=\frac{-1}{3}\]
\[1,-\frac{1}{3},\frac{1}{{{3}^{2}}},-\frac{1}{{{3}^{3}}}...\]
Tổng của cấp số nhân này là: \[S=\frac{{{u}_{1}}}{1-q}=\frac{1}{1+\frac{1}{3}}=\frac{3}{4}\]
- Cấp số nhân lùi vô hạn có số hạng đầu là \[{{u}_{1}}=\frac{1}{2}\] và công bội dương là \[q=\frac{1}{2}\]
\[\frac{1}{2},\frac{1}{{{2}^{2}}},\frac{1}{{{2}^{3}}},\frac{1}{{{2}^{4}}}...\]
Tổng là: \[S=\frac{{{u}_{1}}}{1-q}=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1\]
Câu 5: trang 142 sgk toán Đại số và giải tích 11
Tính các giới hạn sau
a. \[\underset{x\to 2}{\mathop{\lim }}\,\frac{x+3}{{{x}^{2}}+x+4}\]
b. \[\underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x+6}{{{x}^{2}}+3x}\]
c. \[\underset{x\to {{4}^{-}}}{\mathop{\lim }}\,\frac{2x-5}{x-4}\]
d. \[\underset{x\to +\infty }{\mathop{\lim }}\,(-{{x}^{3}}+{{x}^{2}}-2x+1)\]
e. \[\underset{x\to -\infty }{\mathop{\lim }}\,\frac{x+3}{3x-1}\]
f. \[\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}-2x+4}-x}{3x-1}\]
Lời giải
a. \[\underset{x\to 2}{\mathop{\lim }}\,\frac{x+3}{{{x}^{2}}+x+4}=\frac{2+3}{{{2}^{2}}+2+4}=\frac{1}{2}\]
b. \[b)\underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x+6}{{{x}^{2}}+3x}=\underset{x\to -3}{\mathop{\lim }}\,\frac{(x+2)(x+3)}{x(x+3)}\]
\[=\underset{x\to -3}{\mathop{\lim }}\,\frac{x+2}{x}\]
\[=\frac{-3+2}{-3}=\frac{1}{3}\]
c. Ta có: \[\underset{x\to {{4}^{-}}}{\mathop{\lim }}\,(2x-5)=3>0\] ; 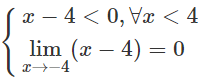
\[\Rightarrow \underset{x\to {{4}^{-}}}{\mathop{\lim }}\,\frac{2x-5}{x-4}=-\infty \]
d. \[\underset{x\to +\infty }{\mathop{\lim }}\,(-{{x}^{3}}+{{x}^{2}}-2x+1)\]
\[=\underset{x\to +\infty }{\mathop{\lim }}\,{{x}^{3}}(-1+\frac{1}{x}-\frac{2}{{{x}^{2}}}+\frac{1}{{{x}^{3}}})=-\infty \]
e. \[e)\underset{x\to -\infty }{\mathop{\lim }}\,\frac{x+3}{3x-1}=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{x(1+\frac{3}{x})}{x(3-\frac{1}{x})}\]
\[=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{1+\frac{3}{x}}{3-\frac{1}{x}}=\frac{1}{3}\]
f. \[\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}-2x+4}-x}{3x-1}\]
\[=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{|x|\sqrt{1-\frac{2}{x}+\frac{4}{{{x}^{2}}}}-x}{3x-1}\]
\[=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{|x|\sqrt{1-\frac{2}{x}+\frac{4}{{{x}^{2}}}}-x}{3x-1}\]
\[=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{-\sqrt{1-\frac{2}{x}+\frac{4}{{{x}^{2}}}}-1}{3-\frac{1}{x}}=\frac{-2}{3}\]
Câu 6: trang 142 sgk toán Đại số và giải tích 11
Cho hai hàm số \[f(x)=\frac{1-{{x}^{2}}}{{{x}^{2}}}\] và \[g(x)=\frac{{{x}^{3}}+{{x}^{2}}+1}{{{x}^{2}}}\]
a) Tính \[\underset{x\to 0}{\mathop{\lim }}\,f(x);\underset{x\to 0}{\mathop{\lim }}\,g(x);\underset{x\to +\infty }{\mathop{\lim }}\,f(x);\underset{x\to +\infty }{\mathop{\lim }}\,g(x)\]
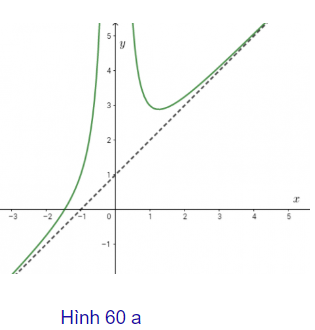
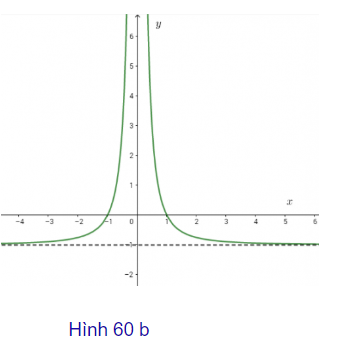
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường cong nào là đồ thị của mỗi hàm số đó.
Lời giải
a)
+) \[\underset{x\to 0}{\mathop{\lim }}\,f(x)=\underset{x\to 0}{\mathop{\lim }}\,\frac{1-{{x}^{2}}}{{{x}^{2}}}=+\infty \]
Vì: \[\underset{x\to 0}{\mathop{\lim }}\,(1-{{x}^{2}})=1>0,\]
\[\underset{x\to 0}{\mathop{\lim }}\,{{x}^{2}}=0;{{x}^{2}}>0,\forall x\ne 0\]
+) \[\underset{x\to 0}{\mathop{\lim }}\,g(x)=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{3}}+{{x}^{2}}+1}{{{x}^{2}}}=+\infty \]
Vì: \[\underset{x\to 0}{\mathop{\lim }}\,({{x}^{3}}+{{x}^{2}}+1)=1>0,\underset{x\to 0}{\mathop{\lim }}\,{{x}^{2}}=0,{{x}^{2}}>0,\]\[\forall x\ne 0\]
\[\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{1-{{x}^{2}}}{{{x}^{2}}}\]
\[=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{{{x}^{2}}(\frac{1}{{{x}^{2}}}-1)}{{{x}^{2}}}=\underset{x\to +\infty }{\mathop{\lim }}\,(\frac{1}{{{x}^{2}}}-1)=-1\]
\[\underset{x\to +\infty }{\mathop{\lim }}\,g(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{{{x}^{3}}+{{x}^{2}}+1}{{{x}^{2}}}\]
\[=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{{{x}^{3}}(1+\frac{1}{x}+\frac{1}{{{x}^{3}}})}{{{x}^{3}}(\frac{1}{x})}\]
\[=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{1+\frac{1}{x}+\frac{1}{{{x}^{3}}}}{\frac{1}{x}}=+\infty \]
b) Gọi (C1) và (C2) lần lượt là hai đồ thị của hàm số y=f(x) và y=g(x)
Vì 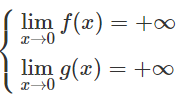
nên hai đồ thị (C1) và (C2) có nhánh đi lên khi x→0.
+) Vì \[\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=-1\] nên (C1) có nhánh tiến gần đến đường thẳng y=−1khi x→∞. Ta thấy giống đặc điểm của đồ thị b
+) Vì \[\underset{x\to +\infty }{\mathop{\lim }}\,g(x)=+\infty \] (C2) có nhánh đi lên khi x→+∞. Ta thấy giống đặc điểm của đồ thị a.
Vậy đồ thị hình b là đồ thị của hàm số \[f(x)=\frac{1-{{x}^{2}}}{{{x}^{2}}}\] và hình a là đồ thị của hàm số \[g(x)=\frac{{{x}^{3}}+{{x}^{2}}+1}{{{x}^{2}}}\]
Câu 7: trang 143 sgk toán Đại số và giải tích 11
Xét tính liên tục trên R của hàm số: .png)
Lời giải
Ta có: \[\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,g(x)=\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\frac{{{x}^{2}}-x-2}{x-2}\]
\[=\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\frac{(x-2)(x+1)}{x-2}\]
\[=\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,(x+1)=3(1)\]
\[\underset{x\to {{2}^{-}}}{\mathop{\lim }}\,g(x)=\underset{x\to {{2}^{-}}}{\mathop{\lim }}\,(5-x)=3(2)\]
\[g(2)=52=3(3)\]
Từ (1), (2) và (3) suy ra: \[\underset{x\to 2}{\mathop{\lim }}\,g(x)=g(2)\]
⇒hàm số y=g(x)liên tục tại x0=2
Ta lại có:
Trên (−∞,2), g(x) là hàm đa thức
Trên (2,+∞), g(x) là hàm số phân thức hữu tỉ xác định trên (2,+∞)
⇒hàm số g(x) liên tục trên hai khoảng (−∞,2) và (2,+∞)
Vậy hàm số y=g(x) liên tục trên R.
Câu 8: trang 143 sgk toán Đại số và giải tích 11
Chứng minh rằng phương trình \[{{x}^{5}}3{{x}^{4}}+5x2=0\] có ít nhất ba nghiệm nằm trong khoảng (−2,5)
Lời giải
Đặt \[f(x)={{x}^{5}}3{{x}^{4}}+5x2\] , ta có:
.png)
Hàm số f(x) là hàm số đa thức liên tục trên R.
⇒ Hàm số f(x) liên tục trên các đoạn [0,1],[1,2],[2,3]
Vậy phương trình \[{{x}^{5}}3{{x}^{4}}+5x2=0\] có ít nhất một nghiệm trên mỗi khoảng (0,1),(1,2),(2,3).
Vậy phương trình \[{{x}^{5}}3{{x}^{4}}+5x2=0\] có ít nhất ba nghiệm trên khoảng (−2,5) (đpcm
