Bài 1 (trang 113 SGK Hình học 11): Cho ba mặt phẳng (α), (β), (γ), những mệnh đề nào sau đây đúng?
a) Nếu (α) ⊥ (β) và (α) // (γ) thì (β) ⊥ (γ).
b) Nếu (α) ⊥ (β) và (α) ⊥ (γ) thì (β) // (γ).
Lời giải:
a) Đúng, vì nếu gọi m là đường thẳng vuông góc với β và n là đường thẳng vuông góc với hai mặt phẳng song song α, γ thì góc (m, n) = (β, α) = (β, γ), mà β ⊥ α nên β ⊥ γ.
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
Bài 2 (trang 113 SGK Hình học 11): Cho hai mặt phẳng (α), (β) vuông góc với nhau. Người ta lấy trên giao tuyến Δ của hai mặt phẳng đó hai điểm A và B sao cho AB = 8cm. Gọi C là một điểm trên (α) và D là một điểm trên (β) sao cho AC và BD cùng vuông góc với giao tuyến Δ và AC = 6cm, BD = 24cm. Tính độ dài đoạn CD.
Lời giải:
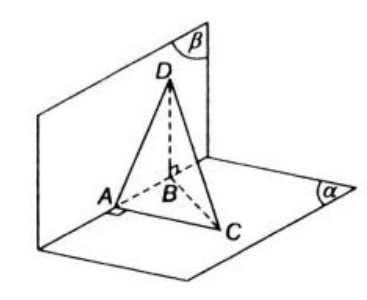
Ta có:
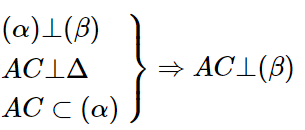
Do đó AC⊥AD hay tam giác ACD vuông tại A
Áp dụng định lí Pytago vào tam giác ACD ta có:
\[C{{D}^{2}}=A{{C}^{2}}+A{{D}^{2}}(1)\]
Theo giả thiết BD vuông góc với giao tuyến nên BD⊥AB hay tam giác ABDvuông tại B.
Áp dụng định lí Pytago vào tam giác ABD ta được:
\[A{{D}^{2}}=A{{B}^{2}}+B{{D}^{2}}(2)\]
Từ (1) và (2) suy ra: \[C{{D}^{2}}=A{{C}^{2}}+A{{B}^{2}}+B{{D}^{2}}={{6}^{2}}+{{8}^{2}}+{{24}^{2}}=676\]
\[\Rightarrow DC=\sqrt{676}=26cm\]
Bài 3 (trang 113 SGK Hình học 11): Trong mặt phẳng (α) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với (α) tại A. Chứng minh rằng:
a) (ABD) là góc giữa hai mặt phẳng (ABC) và (DBC)
b) HK // BC với H và K lần lượt là giao điểm của DB và DC với mp(P) đi qua A và vuông góc với DB.
Lời giải:
.png)
a) Tam giác ABC vuông tại B(gt) nên AB⊥BC (1)
AD vuông góc với (α) (gt) nên AD⊥BC (2)
Từ (1) và (2) ta có:
.png)
mà BD⊂(ABD) suy ra BC⊥BD
Ta có: (ABC)∩(DBC)=BC, AB⊥BC, BC⊥BD
=> Góc giữa hai mặt phẳng (ABC) và (DBC) là \[\widehat{AB,BD}=\widehat{ABD}\] (đpcm)
b) Ta có:
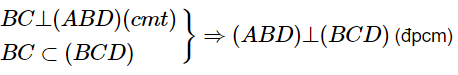
c) Ta có: HK⊂(P) mà (P) đi qua A và vuông góc với BD nên HK⊥BD
Trong (BCD) có: HK⊥BD và BC⊥BD nên suy ra HK//BC.
Bài 4 (trang 114 SGK Hình học 11): Cho hai mặt phẳng (α), (β) cắt nhau và một điểm M không thuộc (α) và (β). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với (α) và (β). Nếu (α) // (β) thì kết quả trên sẽ thay đổi như thế nào?
Lời giải:
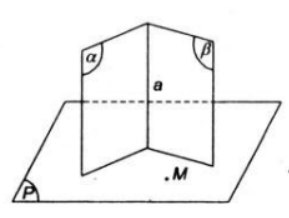
Điều kiện cần: Qua M có một mặt phẳng (P) vuông góc với (α) và (β)
Gọi a=(α)∩(β). Gọi (P) là mặt phẳng đi qua M và vuông góc với a.
Vì a⊂(α) nên (P)⊥(α), a⊂(β) nên (P)⊥(β) (Tính chất: mặt phẳng vuông góc với giao tuyến của hai mặt phẳng thì vuông góc với từng mặt phẳng)
Như vậy qua M có mặt phẳng (P) vuông góc với (α) và (β).
Điều kiện đủ: Mặt phẳng (P) là duy nhất.
Nếu có (P) đi qua M và vuông góc với (α) và (β) thì (P)⊥a. Do tính duy nhất của mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước nên (P) duy nhất.
.png)
Nếu (α)//(β) thì: gọi d là đường thẳng đi qua M và vuông góc với (α) khi đó ta có d⊥(β). Như vậy mọi mặt phẳng chứa d đều vuông góc với (α) và (β).
Do đó khi (α)//(β) thì có vô số mặt phẳng (P) đi qua M và vuông góc với (α) và (β).
Bài 5 (trang 114 SGK Hình học 11): Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:
a) Mặt phẳng (AB'C'D) vuông góc với (BCD'A')
b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD)
Lời giải:

a) Ta có: BC⊥(ABB′A′) (tính chất hình lập phương), AB′⊂(ABB′A′)
⇒BC⊥AB′;
Mà BA′⊥AB′ (đường chéo hình vuông ABB'A')
.png)
Ta có AB′⊂(AB′C′D) nên (AB′C′D)⊥(BCD′A′).
b)
- AA′⊥(ABCD)⇒AA′⊥BD
Mà BD⊥AC,AC∩AA′⇒BD⊥(ACC′A′)
AC′⊂(ACC′A′) nên suy ra BD⊥AC′ (1)
- AB⊥(ADD′A′)⇒AB⊥A′D
Mà AD′⊥A′D⇒A′D⊥(ABC′D′)
Ta có AC′⊂(ABC′D′)⇒AC′⊥A′D (2)
Từ (1) và (2) ta có:
.png)
Bài 6 (trang 114 SGK Hình học 11: Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
Lời giải:
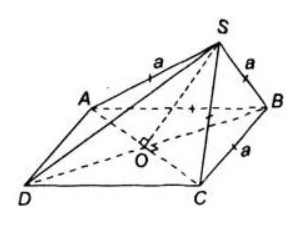
a) Gọi O là giao điểm của hai đường chéo AC và BD
Theo tính chất của hình thoi thì O là trung điểm của AC,BD
Tam giác cân SAC có SA=SC(gt)
=> ΔSAC cân tại S có SO vừa là đường trung tuyến đồng thời là đường cao.
=> SO⊥AC (1)
Mặt khác ABCD là hình thoi nên AC⊥BD (2)
Từ (1) và (2) suy ra .png)
mà AC⊂(ABCD)⇒(ABCD)⊥(SBD)
b) Xét ΔSACvàΔBAC có:
ACchung
SA=AB(=a);SC=BC=(a)
=> ∆SAC=∆BAC(c.c.c)
Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau
=> SO=BO
Vì O là trung điểm của BD nên \[OB=OD=\frac{1}{2}.BD\]
Suy ra \[SO=\frac{1}{2}.BD\]
> Tam giác SBD vuông tại S (Đường trung tuyến ứng với một cạnh của tam giác và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)
Bài 7 (trang 114 SGK Hình học 11): Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có AB = a, BC= b, CC'= c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b và c.
Lời giải:
.png)
a) Ta có: DA⊥(ABB′A′) (tính chất hình hộp)
DA⊂(ADC′B′)
⇒(ADC′B′)⊥(ABB′A′).
b) Ta có: CC′⊥(ABCD) (tính chất hình hộp)
AC⊂(ABCD)
⇒AC⊥CC′
=> tam giác ACC′ vuông tại C
Suy ra \[A{{C}^{2}}+C{{{C}'}^{2}}=A{{{C}'}^{2}}\] (định lý Pytago) (1)
Mặt khác, ΔABC vuông tại B => \[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\] (định lý Pytago)
Thay vào (1) ta suy ra:
\[A{C}'=\sqrt{A{{C}^{2}}+C{{{{C}'}}^{2}}}=\sqrt{A{{B}^{2}}+B{{C}^{2}}+C{{{{C}'}}^{2}}}\]
\[=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}.\]
Bài 8 (trang 114 SGK Hình học 11): Tính độ dài đường chéo của một hình lập phương cạnh a.
Lời giải:
.png)
Hình hộp chữ nhật có độ dài đường chéo là: \[A{C}'=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\]
Hình lập phương là hình hộp chữ nhật có \[a=b=c\] nên ta có đường chéo
\[A{C}'=\sqrt{{{a}^{2}}+{{a}^{2}}+{{a}^{2}}}=\sqrt{3{{a}^{2}}}=a\sqrt{3}\]
Bài 9 (trang 114 SGK Hình học 11)): Cho hình hộp tam giác đều S.ABC có SH là đường cao. Chứng minh SA vuông góc với BC và SB vuông góc với AC.
Lời giải:
.png)
Chóp tam giác đều nên ta có H là trực tâm của tam giác ABC
SH⊥(ABC⇒SH⊥BC
Và AH⊥BC (vì H là trực tâm)
Suy ra BC⊥(SAH)
SA⊂(SAH)⇒BC⊥SA
Chứng minh tương tự, ta có:
SH⊥(ABC)⇒SH⊥AC
Mà H là trực tâm của tam giác ABC ⇒BH⊥AC⇒BH⊥AC
⇒AC⊥(SBH);SB⊂(SBH)⇒AC⊥SB
Bài 10 (trang 114 SGK Hình học 11): Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Lời giải:
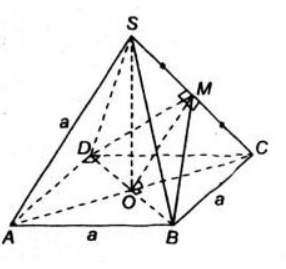
a) Hình chóp tứ giác đều nên SO⊥(ABCD). Do đó SO⊥AC
Xét tam giác SOA vuông tại O:
\[SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\frac{a\sqrt{2}}{2}.\]
b) BD⊥AC , BD⊥SO nên BD⊥(SAC),
Mà BD⊂(MBD) do đó (MBD)⊥(SAC).
c) \[OM=\frac{SC}{2}=\frac{a}{2}\] (trung tuyến ứng với cạnh huyền của tam giác vuông thì bằng nửa cạnh ấy).
\[\text{ }\!\!\Delta\!\!\text{ }SDC=\text{ }\!\!\Delta\!\!\text{ }SBC(c.c.c)\]
suy ra DM=BMsuy ra tam giác BDM cân tại M
OM vừa là trung tuyến đồng thời là đường cao nên OM⊥BD
.png) nên góc giữa hai mặt phẳng (MBD) và (ABCD) là \[\widehat{MOC}\]
nên góc giữa hai mặt phẳng (MBD) và (ABCD) là \[\widehat{MOC}\]
Ta có \[OM=\frac{SC}{2}=\frac{a}{2}\] hay \[OM=MC\] Tam giác OMC vuông cân tại M
\[(\widehat{(MBD);(ABCD)})=(\widehat{MOC})={{45}^{0}}.\]
Bài 11 (trang 114 SGK Hình học 11):
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng 600, cạnh \[SC=\frac{a\sqrt{6}}{2}\] và SC vuông góc với mặt phẳng (ABCD).
a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC).
b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK
c) Chứng minh góc BKD=900 và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD).
Lời giải
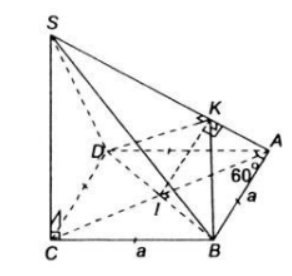
SC vuông góc với mặt phẳng (ABCD) suy ra SC⊥BD (1)
ABCD là hình thoi nên AC⊥BD (2)
Từ (1) và (2) suy ra BD⊥(SAC)
BD⊂(SBD)⇒(SBD)⊥(SAC).
b) Xét tam giác vuông ABI có: \[cos\widehat{IAB}=\frac{AI}{AB}=>AI=AB.cos\widehat{IAB}=AB.\frac{1}{2}.\widehat{IAB}\]
=>\[AI=AB.\cos {{30}^{0}}=\frac{a\sqrt{3}}{2}\Rightarrow AC=2AI=a\sqrt{3}\]
Xét tam giác vuông SAC có: \[SA=\sqrt{A{{C}^{2}}+S{{C}^{2}}}=\sqrt{3{{a}^{2}}+\frac{6{{a}^{2}}}{4}}=\frac{3a}{\sqrt{2}}.\]
Hai tam giác vuông SCA và IKA có:
\[\hat{A}\] chung ; \[\hat{C}=\hat{K}={{90}^{0}}\]
=>\[\Delta SCA\tilde{\ }\Delta IKA(g-g)\]
=>\[\frac{IK}{SC}=\frac{AI}{AS}\Rightarrow IK=\frac{AI.SC}{AS}=\frac{a}{2}.\]
c) IK=IB=ID=a2 nên tam giác BKD vuông tại K. (tam giác có trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì tam giác đó vuông)
Vậy \[\widehat{BKD}={{90}^{0}}.\]
Ta có: SA vuông góc với BD (do BD⊥(SAC)−cmt) và SA⊥IK(gt) nên SA⊥(DKB) => SA⊥DK.
Vì: DK và BK cùng vuông góc với SA. Vậy góc \[\widehat{BKD}\] là góc giữa (SAD) và (SAB) và \[\widehat{BKD}={{90}^{0}}\]\[\Rightarrow (SAD)\bot (SAB)\]
