Bài 1 (trang 121 SGK Hình học 11): Trong các mệnh đề sau đây, mệnh đề nào là đúng?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song;
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song;
c) Mặt phẳng (α) vuông góc với đường thẳng b và b vuông góc với thẳng a, thì a song song với (α).
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.
Lời giải:
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng a và b cùng ở trong mp(P) và mp(α) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Bài 2 (trang 121 SGK Hình học 11): Trong các điều khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Lời giải:
Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Bài 3 (trang 121 SGK Hình học 11): Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
Lời giải:
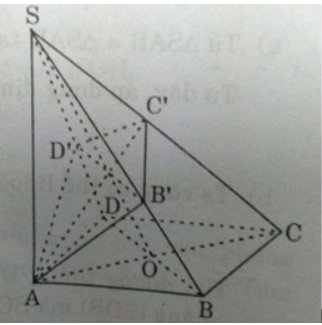
a)
- Chứng minh ΔSAB vuông
Ta có: SA⊥(ABCD),AB⊂(ABCD)=>SA⊥AB=>ΔSABvuông
- Chứng minh ΔSAD vuông
Ta có: SA⊥(ABCD),AD⊂(ABCD)=>SA⊥AD=>ΔSADvuông
- Chứng minh ΔSBC vuông
SA⊥(ABCD) nên AB là hình chiếu của SB trên mp(ABCD)
ABCD là hình vuông nên BC⊥AB.
Ta có:
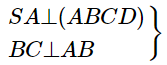
⇒SB⊥BC (theo định lí ba đường vuông góc)
⇒ΔSBC là tam giác vuông tại B
- Chứng minh ΔSCD vuông
SA⊥(ABCD) nên AD là hình chiếu của SD trên mp(ABCD)
ABCD là hình vuông nên CD⊥AD.
Ta có:
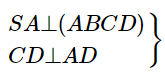
⇒SD⊥CD (theo định lí ba đường vuông góc)
⇒ΔSCD là tam giác vuông tại D
b)
- Chứng minh B′D′//BD
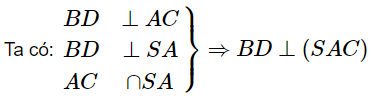
mà SC⊂(SAC)⇒BD⊥SC
Mặt khác: (α)⊥SC(gt)⇒BD//(α)
Ta có: (SBD)∩(α)=B′D′
=> B′D′//BD
- Chứng minh: AB′⊥SB
Vì BC⊥(SAB),AB′⊂(SAB)⇒BC⊥AB′ (1)
SC⊥(α),AB′⊂(α)⇒SC⊥AB′ (2)
Từ (1) (2) suy ra AB′⊥(SBC)⇒AB′⊥SB
Bài 4 (trang 121 SGK Hình học 11): Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc BAD = 60o. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = 3a/4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
Lời giải:
.png)
a) Theo giả thiết hình thoi ABCD có: BADˆ=600 => BCDˆ=600
suy ra tam giác BCD đều => CBDˆ=600 hay OBCˆ=600
ABCD là hình thoi => AC⊥BD≡O => ΔBOC vuông tại O có E là trung điểm BC
=> OE=EB=EC=\[\frac{1}{2}\]BC (tính chất đường trung tuyến ứng với cạnh huyền)
Xét tam giác BOE có BO=BE−cmt và OBEˆ=600 nên tam giác BOE đều
Có F là trung điểm BD => OF đồng thời là đường cao => OF⊥BC.
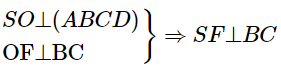(Định lí 3 đường vuông góc)
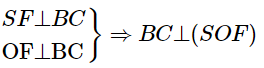
Mà BC⊂(SBC)
Suy ra (SOF)⊥(SBC)
b) Vì (SOF)⊥(SBC) và hai mặt phẳng này giao nhau theo giao tuyến SF
nên từ O ta kẻ OH⊥SF => OH⊥(SBC) => d(O,(SBC))=OH
Ta có:
\[SO=\frac{3a}{4};\text{OF=}\frac{a\sqrt{3}}{4}\Rightarrow SF=\frac{a\sqrt{3}}{2}\]
\[OH.SF=SO.\text{OF}\Rightarrow \text{OH=}\frac{3a}{8}\]
Trong ΔAKC thì OH là đường trung bình, do đó:
\[AK=2OH\Rightarrow AK=\frac{3a}{4}\]
Bài 5 (trang 121 SGK Hình học 11): Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có A vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của Ad và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
Lời giải:
.png)
a)
- Chứng minh ΔBAD vuông
Theo giả thiết: (ABC)⊥(ADC) mà hai mặt phẳng này giao nhau theo giao tuyến AC.
Ta lại có BA⊂(ABC) và BA⊥AC nên BA⊥(ADC)
Vì AB⊂(ADC)⇒BA⊥AD⇒ΔBAD vuông tại A
- Chứng minh: ΔBCD vuông
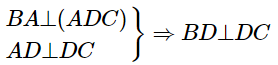(Định lí 3 đường vuông góc)
⇒ΔBDC vuông tại D
b) Chứng minh: IK là đoạn vuông góc chung của AD,BC
Xét ΔABC và ΔCAD có:
\[\hat{A}=\hat{D}\]
AC chung
AB=CD=a
=> ΔABC=ΔCAD(c−g−c)
=> BI=CI (hai trung tuyến tương ứng của hai tam giác bằng nhau)
=> ΔIBC cân tại I
có: K là trung điểm BC => IK đồng thời là đường cao trong ΔIBC
=> IK⊥BC (1)
Chứng minh tương tự, ta có: ΔABC=ΔDCB(c−g−c)
=> AK=DK
=> ΔKAD cân tại K
có: I là trung điểm AD => KI đồng thời là đường cao trong ΔKAD
=> KI⊥AD (2)
Từ (1) (2) => KI là đoạn vuông góc chung của AD.BC.
Bài 6 (trang 121 SGK Hình học 11): Cho khối lập phương ABCD.A'B'C'D' cạnh a.
a) Chứng minh BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'.
Lời giải:
.png)
a) Ta có tứ giác BCC′B′ là hình vuông nên
BC′⊥B′C (1)
Mặt khác A′B′⊥(BCC′B′)
⇒A′B′⊥BC′ (2)
Từ (1) và (2) suy ra: BC′⊥(A′B′C′D′)
b) Do AD′//BC′ nên mặt phẳng (AB′D′) là mặt phẳng chứa AB′ và song song với BC′.
Ta tìm hình chiếu của BC′ trên mp(AB′D′)
Gọi E,F là tâm của các mặt bên ADD′A′ và BCC′B′
Từ F kẻ FI⊥B′E. Ta có BC′//AD′ mà BC′⊥(A′B′CD)
⇒AD′⊥(A′B′CD) và IF⊂(A′B′CD)
AD′⊥IF (3)
EB′⊥IF (4)
Từ (3) và (4) suy ra : IF⊥(AB′D′)
Vậy I là hình chiếu của F trên mp(AB′D′). Qua I ta dựng đường thẳng song song với BC′ thì đường thẳng này chính là hình chiếu của BC′ trên mp (AB′D′)
Đường thẳng qua I song song với BC′ cắt AB′ tại K. Qua K kẻ đường thẳng song song với IF, đường này cắt BC′ tại H. KH chính là đường vuông góc chung của AB′ và BC′. Thật vậy:
IF⊥(AB′D′)
⇒IF⊥AB′ và KH//IF suy ra KH⊥AB′
.png)
Tam giác EFB′ vuông góc tại F, FI là đường cao thuộc cạnh huyền nên
\[\frac{1}{I{{F}^{2}}}=\frac{1}{F{{B}^{2}}}+\frac{1}{F{{E}^{2}}}\] với
.png)
Ta tính ra: \[\text{IF}=\frac{a\sqrt{3}}{3}\Rightarrow KH=\text{IF=}\frac{a\sqrt{3}}{3}\]
Bài 7 (trang 121 SGK Hình học 11): Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc \[\widehat{BAD}={{60}^{0}}\] và \[SA=SB=SD=\frac{a\sqrt{3}}{2}\]
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với SC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Lời giải:
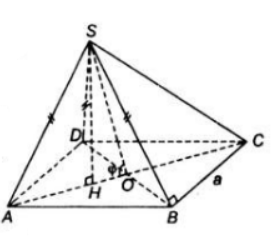
a) Kẻ SH⊥(ABCD)
Do SA=SB=SD suy ra HA=HB=HC
⇒H là tâm đường tròn ngoại tiếp tam giác ABD.
Do AB=AD=a và \[\widehat{BAD}={{60}^{0}}\] nên tam giác ABD là tam giác đều cạnh a,
Ta có:
\[AO=\frac{a\sqrt{3}}{2}\], \[AH=\frac{2}{3}AO\Rightarrow AH=\frac{a\sqrt{3}}{3}\]
Trong tam giác vuông SAH, ta có: \[SA=\frac{a\sqrt{3}}{2};AH=\frac{a\sqrt{3}}{3}\]
Tính ra: \[SH=\frac{a\sqrt{15}}{6}\]
Ta cũng có \[HC=\frac{2a\sqrt{3}}{3}\]
Trong tam giác vuông SHC: \[S{{C}^{2}}=S{{H}^{2}}+H{{C}^{2}}\]
Do đó ta tính được: \[SC=\frac{a\sqrt{7}}{2}\]
b)
.png)
c) Ta có:
\[S{{C}^{2}}=\frac{7{{a}^{2}}}{4}(1)\]
\[B{{C}^{2}}={{a}^{2}}(2)\]
\[S{{B}^{2}}=\frac{3{{a}^{2}}}{4}(3)\]
Từ (1), (2) và (3) ta có: \[S{{C}^{2}}=B{{C}^{2}}+S{{B}^{2}}\]
Theo định lí Pytago đảo, tam giác SBC vuông tại B.
d) Ta có:
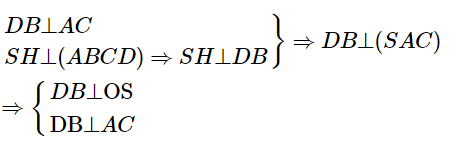
Suy ra: \[\widehat{SOH}\] là góc giữa hai mặt phẳng (SBD) và (ABCD)
Ta có:
\[\widehat{SOH}=\varphi \]
\[\tan \varphi =\frac{SH}{OH}\Rightarrow \tan \varphi =\sqrt{5}\]