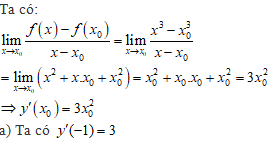Bài 1 (trang 156 SGK Đại số 11): Tìm số gia của hàm số f(x) = x3, biết rằng:
a. x0 = 1; Δx = 1;
b. x0 = 1; Δx = -0,1;
Lời giải:
Số gia của hàm số được tính theo công thức:
Δy = f(x) – f(x0) = f(x0 + Δx) – f(x0)
a. Δy = f(1 + 1) – f(1) = f(2) – f(1) = 23 – 13 = 7
b. Δy = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)3 – 13 = -0,271.
Bài 2 (trang 156 SGK Đại số 11): Tính\[\vartriangle y\] và \[\frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}\] của các hàm số sau theo x và \[\vartriangle x\]
a) \[y=2x-5\] b) \[y={{x}^{2}}-1\]
c) \[y=2{{x}^{3}}\] d) \[y=\frac{1}{x}\]
Lời giải
a) \[\vartriangle y\text{ }=\text{ }f\left( x+\vartriangle x \right)-f\left( x \right)=2\left( x+\vartriangle x \right)-5-\left( 2x-\text{ }5 \right)=\text{ }2x+2.\vartriangle x-5-2x+5=2.\vartriangle x\]
\[\frac{\Delta y}{\Delta x}=\frac{2\Delta x}{\Delta x}=2\]
b)
\[\Delta y=f(\Delta x+x)-f(x)\]
\[={{(x+\Delta x)}^{2}}-1-({{x}^{2}}-1)\]
\[={{x}^{2}}+2x.?x+{{(\vartriangle x)}^{2}}-1-{{x}^{2}}+1\]
\[=2x.\Delta x+{{(\Delta x)}^{2}}\]
\[=\Delta x(2x+\Delta x)\]
\[\frac{\Delta y}{\Delta x}=\frac{\Delta x\left( 2x+\Delta x \right)}{\Delta x}=2x+\Delta x\]
c) \[\vartriangle y=f(x+\vartriangle x)-f(x)=2{{(x+\vartriangle x)}^{3}}-2{{x}^{3}}\]
\[=2\left[ {{x}^{3}}+3{{x}^{2}}.\vartriangle x+3.x{{(\vartriangle x)}^{2}}+{{(\vartriangle x)}^{3}} \right]-2{{x}^{3}}\]
\[=6{{x}^{2}}\Delta x+6x{{(\Delta x)}^{2}}+2{{(\Delta x)}^{3}}\]
\[=2\Delta x.\left[ 3{{x}^{2}}+3x\Delta x+{{(\Delta x)}^{2}} \right]\]
\[\frac{\Delta y}{\Delta x}=\frac{2\Delta x\left[ 3{{x}^{2}}+3x\Delta x+{{(\Delta x)}^{2}} \right]}{\Delta x}=6{{x}^{2}}+6x?x+2{{(\vartriangle x)}^{2}}\]
d) \[\vartriangle y=f(x+\vartriangle x)-f(x)=-\frac{1}{x}+\frac{1}{x+\Delta x}=\frac{-x-\Delta x+x}{x\left( x+\Delta x \right)}=-\frac{\Delta x}{x\left( x+\Delta x \right)}\]
\[\frac{\Delta y}{\Delta x}=\frac{-\frac{\Delta x}{x\left( x+\Delta x \right)}}{\Delta x}=-\frac{1}{\left( x+\Delta x \right)x}\]
Bài 3 (trang 156 SGK Đại số 11): Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:
\[a)y={{x}^{2}}+x\] tại \[{{x}_{0}}=1\]
\[b)y=\frac{1}{x}\] tại \[{{x}_{0}}=2\]
c) \[y=\frac{x+1}{x-1}\] tại \[{{x}_{0}}=0\]
Lời giải:
a) Giả sử Δx là số gia của số đối tại x0=1. Ta có:
\[\text{ }\!\!\Delta\!\!\text{ }y=f\left( 1+\text{ }\!\!\Delta\!\!\text{ }x \right)-f\left( 1 \right)\]
\[={{\left( 1+\text{ }\!\!\Delta\!\!\text{ }x \right)}^{2}}+\left( 1+\text{ }\!\!\Delta\!\!\text{ }x \right)-{{1}^{2}}-1\]
\[=1+2\text{ }\!\!\Delta\!\!\text{ }x+{{\left( \text{ }\!\!\Delta\!\!\text{ }x \right)}^{2}}+1+\text{ }\!\!\Delta\!\!\text{ }x-2\]
\[=\text{ }\!\!\Delta\!\!\text{ }x\left( \text{ }\!\!\Delta\!\!\text{ }x+3 \right)\]
\[\Rightarrow \frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\text{ }\!\!\Delta\!\!\text{ }x+3\]
\[\Rightarrow \underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\left( \text{ }\!\!\Delta\!\!\text{ }x+3 \right)=3\]
b) Giả sử Δx là số gia của số đối tại x0=2. Ta có:
\[\text{ }\!\!\Delta\!\!\text{ }y=f\left( 2+\text{ }\!\!\Delta\!\!\text{ }x \right)-f\left( 2 \right)\]
\[=\frac{1}{2+\text{ }\!\!\Delta\!\!\text{ }x}-\frac{1}{2}\]
\[=\frac{2-2-\text{ }\!\!\Delta\!\!\text{ }x}{2\left( 2+\text{ }\!\!\Delta\!\!\text{ }x \right)}=\frac{-\text{ }\!\!\Delta\!\!\text{ }x}{2\left( 2+\text{ }\!\!\Delta\!\!\text{ }x \right)}\]
\[\Rightarrow \frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\frac{-1}{2\left( 2+\text{ }\!\!\Delta\!\!\text{ }x \right)}\]
\[\Rightarrow \underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\left( \frac{-1}{2\left( 2+\text{ }\!\!\Delta\!\!\text{ }x \right)} \right)=\frac{-1}{2.2}=-\frac{1}{4}\]
c) Giả sử Δx là số gia của số đối tại x0=0. Ta có:
\[\text{ }\!\!\Delta\!\!\text{ }y=f\left( \text{ }\!\!\Delta\!\!\text{ }x \right)-f\left( 0 \right)\]
\[=\frac{\text{ }\!\!\Delta\!\!\text{ }x+1}{\text{ }\!\!\Delta\!\!\text{ }x-1}-\frac{0+1}{0-1}\]
\[=\frac{\text{ }\!\!\Delta\!\!\text{ }x+1}{\text{ }\!\!\Delta\!\!\text{ }x-1}+1\]
\[=\frac{\text{ }\!\!\Delta\!\!\text{ }x+1+\text{ }\!\!\Delta\!\!\text{ }x-1}{\text{ }\!\!\Delta\!\!\text{ }x-1}=\frac{2\text{ }\!\!\Delta\!\!\text{ }x}{\text{ }\!\!\Delta\!\!\text{ }x-1}\]
\[\Rightarrow \frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\frac{2}{\text{ }\!\!\Delta\!\!\text{ }x-1}\]
\[\Rightarrow \underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\frac{\text{ }\!\!\Delta\!\!\text{ }y}{\text{ }\!\!\Delta\!\!\text{ }x}=\underset{\text{ }\!\!\Delta\!\!\text{ }x\to 0}{\mathop{\lim }}\,\left( \frac{2}{\text{ }\!\!\Delta\!\!\text{ }x-1} \right)=\frac{2}{-1}=-2\]
Vậy \[{f}'(0)=-2\]
Bài 4 (trang 156 SGK Đại số 11): Chứng minh rằng hàm số:
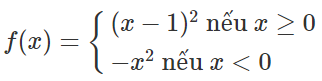
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.
Lời giải:
Ta có:
\[\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{{\left( x-1 \right)}^{2}}={{\left( 0-1 \right)}^{2}}=1\]
\[\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( -{{x}^{2}} \right)=-{{0}^{2}}=0\]
\[\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f\left( x \right)\ne \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)\]
Do đó hàm số \[y=f(x)\] gián đoạn tại x=0.
Vậy hàm số không có đạo hàm tại điểm x=0 (vi phạm điều kiện cần)
Xét giới hạn:
\[\underset{x\to 2}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 2 \right)}{x-2}=\underset{x\to 2}{\mathop{\lim }}\,\frac{{{\left( x-1 \right)}^{2}}-1}{x-2}\]
\[=\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-2x}{x-2}=\underset{x\to 2}{\mathop{\lim }}\,\frac{x\left( x-2 \right)}{x-2}=\underset{x\to 2}{\mathop{\lim }}\,x=2\].
Vậy hàm số \[y=f(x)\] có đạo hàm tại x=2 và \[{f}'(2)=2\]
Bài 5 (trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến đường cong y = x3
a. Tại điểm (-1; -1);
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Lời giải:
Ta có:
\[\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{{{x}^{3}}-x_{0}^{3}}{x-{{x}_{0}}}\]
\[=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\left( {{x}^{2}}+x.{{x}_{0}}+x_{0}^{2} \right)=x_{0}^{2}+{{x}_{0}}.{{x}_{0}}+x_{0}^{2}=3x_{0}^{2}\]
\[\Rightarrow {y}'\left( {{x}_{0}} \right)=3x_{0}^{2}\]
a) Ta có \[{y}'(-1)=3\]
Vậy phương trình tiếp tuyến tại điểm (-1;-1) là: \[y=3\left( x+1 \right)-1=3x+2\]
b) Ta có: \[{y}'(2)={{3.2}^{2}}=12\]; \[y(2)={{2}^{3}}=8\]
Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng 2 là:
\[y=12\left( x-2 \right)+8=12x-16\]
c) Gọi x0 là hoành độ tiếp điểm. Ta có:
\[{y}'({{x}_{0}})=3\Leftrightarrow 3{{x}_{0}}^{2}=3\Leftrightarrow {{x}_{0}}^{2}=1\Leftrightarrow {{x}_{0}}=\pm 1\]
+) Với \[{{x}_{0}}=1\] ta có \[y(1)=1\], phương trình tiếp tuyến là \[y=3\left( x-1 \right)+1=3x-2\]
+) Với \[{{x}_{0}}=-1\] ta có \[y(-1)=-1\], phương trình tiếp tuyến là \[y=3\left( x+1 \right)-1=3x+2\]
Bài 6 (trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến của hypebol y = 1/x
a) Tại điểm \[(\frac{1}{2};2)\]
b) Tại điểm có hoành độ bằng −1
c) Biết rằng hệ số góc của tiếp tuyến bằng -\[\frac{1}{4}\]
Lời giải:
Xét giới hạn:
\[\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{\frac{1}{x}-\frac{1}{{{x}_{0}}}}{x-{{x}_{0}}}\]
\[=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{{{x}_{0}}-x}{x.{{x}_{0}}\left( x-{{x}_{0}} \right)}=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{-1}{x.{{x}_{0}}}=-\frac{1}{x_{0}^{2}}\]
\[\Rightarrow {y}'\left( {{x}_{0}} \right)=-\frac{1}{x_{0}^{2}}\]
a) Ta có: \[{y}'\left( \frac{1}{2} \right)=-4\]
Vậy phương trình tiếp tuyến của hypebol tại điểm \[(\frac{1}{2};2)\] là \[y=-4\left( x-\frac{1}{2} \right)+2=-4x+4\]
b) Ta có: \[{y}'(-1)=-1,y(-1)=-1\]
Vậy phương trình tiếp tuyến tại điểm có tọa độ là −1 là: \[y=-\left( x+1 \right)-1=-x-2\]
c) Gọi x0 là hoành độ tiếp điểm. Ta có
\[{y}'({{x}_{0}})=-\frac{1}{4}\Leftrightarrow -\frac{1}{x_{0}^{2}}=-\frac{1}{4}\]\[\Leftrightarrow x_{0}^{2}=4\Leftrightarrow {{x}_{0}}=\pm 2\]
Vớ \[{{x}_{0}}=2\] ta có \[y(2)=\frac{1}{2}\], phương trình tiếp tuyến là \[y=-\frac{1}{4}\left( x-2 \right)+\frac{1}{2}=-\frac{1}{4}x+1\]
Với \[{{x}_{0}}=-2\] ta có \[y(-2)=-\frac{1}{2}\] , phương trình tiếp tuyến là: \[y=-\frac{1}{4}\left( x+\frac{1}{2} \right)-\frac{1}{2}=-\frac{1}{4}x-1\]
Bài 7 (trang 157 SGK Đại số 11): Một vật rơi tự do theo phương trình s=1/2 gt2, trong đó g≈9,8m/s2 là gia tốc trọng trường.
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t+Δt, trong các trường hợp Δt = 0,1s; Δt = 0,05s; Δt = 0,001s.
b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
Lời giải:
a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t+Δt là
\[{{v}_{tb}}=\frac{s\left( t+\text{ }\!\!\Delta\!\!\text{ }t \right)-s\left( t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}\]
\[=\frac{\frac{1}{2}g{{\left( t+\text{ }\!\!\Delta\!\!\text{ }t \right)}^{2}}-\frac{1}{2}g{{t}^{2}}}{\text{ }\!\!\Delta\!\!\text{ }t}\]
\[=\frac{g{{t}^{2}}+2gt.\text{ }\!\!\Delta\!\!\text{ }t+g\text{ }\!\!\Delta\!\!\text{ }{{t}^{2}}-g{{t}^{2}}}{2\text{ }\!\!\Delta\!\!\text{ }t}\]
\[=\frac{1}{2}g\left( 2t+\text{ }\!\!\Delta\!\!\text{ }t \right)\]
Với t=5 và
+) \[\Delta t=0,1\] thì \[{{v}_{tb}}\approx 4,9.(10+0,1)\approx 49,49m/s\]
+) \[\vartriangle t=0,05\] thì \[{{v}_{tb}}\approx 4,9.(10+0,05)\approx 49,245m/s\]
+) \[\vartriangle t=0,001\] thì \[{{v}_{tb}}\approx 4,9.(10+0,001)\approx 49,005m/s\]
b) Vận tốc tức thời của chuyển động tại thời điểm t=5s tương ứng với Δt=0
nên \[v\approx 4,9.10=49m/s\]